密碼雜湊函數
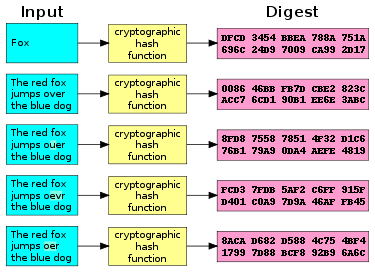
密碼雜湊函數(粵拼:mat6 maa3 zaap6 cau3 haam4 sou3,英文:Cryptographic hash function)喺密碼學入面係種有保密性質嘅雜湊函數,可以用來驗證身份或者檢查重要信息有無俾人篡改。佢嘅輸入係一條無定長短嘅字串(通常叫做消息),輸出係一個固定位數嘅數(叫做雜湊值)。密碼雜湊函數嘅輸出經常用十六進制寫成有固定長度嘅字串,呢種字串會叫做信息摘要(message digest)或者數碼指模(digital fingerprint)。
密碼雜湊函數有下面性質,
- 由消息好容易計出雜湊值;
- 由雜湊值倒推返消息嘅一般算法需要大量計算資源以至於實際上無可能做到;
- 想將個消息改少少,又想雜湊值唔變,現實上無可能;
- 想搵到兩個唔同嘅消息對應同一個雜湊值,現實上無可能。
爾一系列性質(單向性,one-way)保證密碼雜湊函數對基本嘅密碼學攻擊有好嘅抗性,可以用來做好基本嘅資訊保安工夫,喺現代信息社會有非常廣泛嘅應用。密碼雜湊函數亦係密碼學入面單向函數嘅經典例子。
同一般嘅雜湊函數一樣,密碼雜湊函數亦可以用來做信息索引。
應用[編輯]
驗證信息或者文件無俾人篡改[編輯]
例如,有個網站提供個文件俾人下載,有人通過唔安全嘅網絡環境下載咗個文件,想保證個文件傳輸過程中無俾人喐過,噉佢就可以自己計一下個文件嘅數碼指模,然之後同個網站上面寫出來個數碼指模比較一下,如果一樣,就可以放心噉用下載咗嘅文件喇。為咗保證網站道睇到嘅數碼指模本身係信得過,需要有一個加密嘅網絡連接,例如HTTPS。依個過程係密碼學入面信任鏈(chain of trust)嘅一個例子。由於數碼指模係一個好短嘅字串(無論個文件本身幾大,數碼指模都係一行寫得嗮),兼且計起身好快,所以同比較文件內容本身相比,比較數碼指模會有效率好多。
就算唔涉及信息安全,比如話喺部電腦道複製一個好大嘅文件,想知道複製過程中有無出錯,都可以直接比較一下兩個文件嘅數碼指模。
儲低同驗證密碼[編輯]
今時今日用電子產品幾乎道道都離唔開密碼。操作系統同各種網站就需要儲低密碼。將密碼用明文形式儲落個文件道係好唔安全,因為衹要有人攞到個文件啲密碼就通嗮天。但係如果將密碼計出來個數碼指模存低就唔同,就算俾人攞到個文件,都唔會知道原本嘅密碼係乜。另一方面,需要驗證密碼嘅時候,只要計一次輸入嘅密碼嘅數碼指模,再將計出來嘅數碼指模同先前儲低嘅數碼指模比較,就可以知道個密碼啱唔啱。
當然,噉樣做重係唔夠安全,因為黑客手上通常會有一份常用密碼表,如果衹係將密碼本身嘅數碼指模儲低,黑客就可以好容易將手上嗰份常用密碼表嘅數碼指模全部計出來,然之後同攞到個文件裏面嘅數碼指模比較一下,就可以破解大部分密碼。由於而今安全性得到認可嘅密碼雜湊函數總共先得幾種,所以計嗮常用密碼表入面各個密碼嘅各種數碼指模亦唔係難,之後黑客就可以攞住呢份表行遍天下。類似嘅方法重有彩虹表攻擊。
鑑於上面講到嘅呢個問題,好多密碼管理系統都唔係直接將密碼嘅數碼指模儲低,而係會將密碼本身修改之後(最簡單嘅方法係喺密碼前面或者後面加一個隨機生成嘅字串,嗰個字串叫做salt),再將修改密碼嘅算法同埋修改之後嘅密碼嘅數碼指模一齊儲低落文件道。由於修改密碼嘅方法本身可以係千變萬化,所以黑客係無可能事先儲低嗮常用密碼表入面啲密碼經過唔同嘅修改之後嘅數據指模會係怎然之後揸住份表去一個一個對,所以就算俾黑客攞到個文件,佢都需要相當長時間先可以破解出入面儲低嘅常用密碼表入面嘅密碼,至於其它密碼,現實上無可能破到。
零信息證明(Zero-knowledge proof)[編輯]
有個密碼學入面嘅經典例子。阿甲出咗條難題,話佢自己知道答案,想考下阿乙。阿乙有興趣,但係佢覺得條題目太難,阿甲無可能知道答案。阿甲要向阿乙證明佢當時的確知道答案,但又唔想直接將個答案講出來,於是佢將答案嘅數碼指模講畀阿乙聽。阿乙記低咗,返去做咗一輪,計到個答案,之後佢自己計一次個數碼指模,同之前阿甲畀佢嗰個對比一下,就知道阿甲當時有無講大話。呢個過程就係零信息證明。因為阿甲既證明到自己講真話,又無洩漏到問題個答案或者任何有助於推出個答案嘅具體知識。
工作驗證系統 (Proof of work)[編輯]
工作驗證系統係種用來證明某個人的確用咗一定嘅時間去解決某一個一定難度問題嘅系統。佢可以用來防止分散式阻斷服務攻擊。
分散式阻斷服務攻擊係種短時間內向服務器發送大量請求導致服務器癱瘓嘅攻擊。工作驗證系統要求客戶端發送請求之前要先解決由服務器所出嘅一條問題,一般嘅電腦可以喺好短時間內解決呢條問題,即係話用戶唔會留意到解題造成嘅延遲,但係同時個問題大幅提高咗客戶端發請求嘅時間成本,令到客戶端無可能喺短時間內發出大量有效請求。
工作驗證系統亦可以用來對付垃圾郵件。例如,無工作驗證系統,一個惡意用戶可以喺瞬間發出一百萬份垃圾郵件。而工作驗證系統要求每個人發郵件之前先用部電腦來解決一個用時係 0.001 秒嘅問題。噉做嘅話一般用戶發郵件唔會有乜影響,但係個惡意用戶如果想再發出一百萬份垃圾郵件就需要一千秒嘅時間。
密碼雜湊函數喺工作驗證系統裡面可以用來出題。以Bitcoin所用嘅工作驗證系統為例,佢會要求用戶搵到一個消息嘅數碼指模頭幾位全部都係零,兼且人哋經已搵過嘅消息唔可以再用。目前來講,要解決呢個問題衹能夠一個個消息去撞,直到撞到為止,噉就需要一定時間。上面呢個過程就係Bitcoin裡面所謂嘅「挖礦」。挖礦所需要嘅平均時間係可以預計嘅,於是Bitcoin產生嘅速度亦都可以預計,噉樣Bitcoin就唔會因為瞬間產生出太多而大幅貶值。
信息索引[編輯]
同一般雜湊函數一樣,密碼雜湊函數可以用來做信息索引。
例如,版本管理系統經常會用到密碼雜湊函數來做信息索引。系統入面嘅每一個用戶、每一個文件、每一次修改、文件喺唔同時間嘅每一個版本,都會有自己嘅數碼指模。任何人只要攞一個數碼指模畀個系統,唔需要任何其它信息,個系統衹要查表,就可以馬上知道佢係講緊一個用戶,一個文件定係其它。將密碼雜湊函數用來做索引重可以用來保證系統入面嘅內容無辦法偽造。比如想偽造某一個文件嘅修改日期係做唔到,因為產生文件數碼指模嗰陣,密碼雜湊函數嘅輸入經已有齊嗮文作者、修改日期等等信息。
密碼雜湊函數甚至重可以保證文件嘅歷史無俾人篡改。比如一個文件有一百個歷史版本,每一次修改都有唔同作者。有人睇某個作者唔順眼,想喺歷史記錄道整走嗮佢做過嘅修改。如果個版本管理系統無設計成防止歷史被篡改,佢衹要喺個數據庫道刪走嗰幾個版本嘅數碼指模就搞掂。但係如果個版本管理系統喺產生每一個版本嘅數據指模嗰陣,都將上一個版本嘅數據指模放落密碼雜湊函數嘅輸入道,噉就無可能淨係刪走幾個版本而唔改變爾啲版本之後嘅所有版本嘅數據指模喇。
種類[編輯]
| 密碼雜湊函數 | 年份 | 輸出位數 | 內部狀態位數 | 圈數 | 參考 |
|---|---|---|---|---|---|
| HAVAL | 1992 | 256/224/192/160/128 | 256 | 160/128/96 | 網站 |
| MD2 | 1989 | 128 | 384 | 864 | RFC 1319 |
| MD4 | 1990 | 128 | 128 | 48 | RFC 1320 |
| MD5 | 1992 | 128 | 128 | 64 | RFC 1321 |
| MD6 | 2008 | 睇參考 | md6_report.pdf | ||
| RIPEMD | 1990 | 128 | 128 | 48 | |
| RIPEMD-128 RIPEMD-256 RIPEMD-160 RIPEMD-320 |
1996 | 128 256 160 320 |
128 256 160 320 |
48 64 80 |
網站 |
| SHA-0 | 1993 | 160 | 160 | 80 | SHA-0 |
| SHA-1 | 1995 | 160 | 160 | 80 | [1] |
| SHA-256 SHA-512 SHA-384 |
2002 | 256 512 384 |
256 512 512 |
64 80 80 | |
| SHA-224 | 2004 | 224 | 256 | 64 | |
| GOST R 34.11-94 | 1994 | 256 | 256 | 256 | RFC 5831, RFC 4357 |
| Tiger | 1995 | 192/160/128 | 192 | 24 | 網站 |
| Whirlpool | 2004 | 512 | 512 | 10 | 網站 |
| SHA-3 (Keccak) | 2008 | 224/256/384/512 | 1600 | 24 | 網站 |
睇埋[編輯]
參考[編輯]
- 爾篇文部分內容由英文維基百科文章Cryptographic hash function(版本662781013)攞料,並以創意共享之下,署名兼共享版權嘅3.0版本協議授權使用。原文作者請睇嗰版歷史。
- 爾篇文部分內容由英文維基百科文章Comparison of cryptographic hash functions(版本639564314)攞料,並以創意共享之下,署名兼共享版權嘅3.0版本協議授權使用。原文作者請睇嗰版歷史。
