包絡

Construction of the envelope of a family of curves.

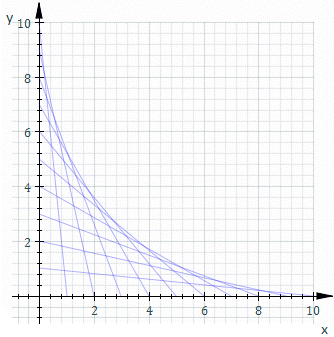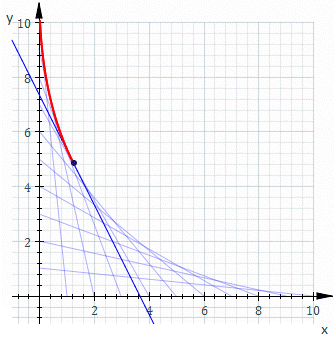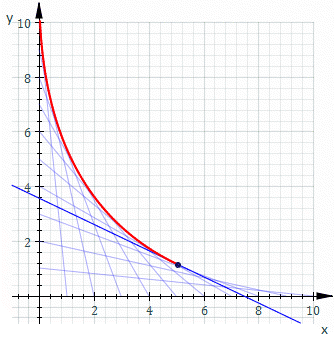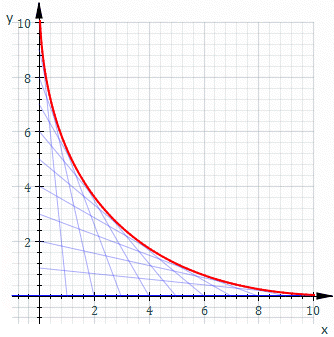
喺幾何上，平面上一族曲線嘅包絡係咁樣一條曲線：喺佢上面每一點處，都有呢族曲線中嘅一條同佢相切。Classically, 包絡上嘅一個點可以認為係兩條「鄰近」曲線嘅交點，即係鄰近曲線嘅交點嘅極限。呢個諗法可以推廣到空間中曲面嘅包絡，同埋更高嘅維數。

一族曲線嘅包絡

設族入面嘅每條曲線C_t由f_t(x, y)=0確定，其中t係參數。記 F(t, x, y)=f_t(x, y)並且假設F可微。

下面段文未譯好，歡迎你幫手。

於是曲線族C_t嘅包絡 is defined as the set of points for which

$F(t,x,y)={\partial F \over \partial t}(t,x,y)=0$

for some value of t, where $\partial F/\partial t$ is the partial derivative of F with respect to t.

Note that if t and u, t≠u are two values of the parameter then the intersection of the curves C_t and C_u is given by

$F(t,x,y)=F(u,x,y)=0\,$

or equivalently

$F(t,x,y)={\frac {F(u,x,y)-F(t,x,y)}{u-t}}=0.$

Letting u→t gives the definition above.

An important special case is when F(t, x, y) is a polynomial in t. This includes, by clearing denominators, the case where F(t, x, y) is a rational function in t. In this case, the definition amounts to t being a double root of F(t, x, y), so the equation of the envelope can be found by setting the discriminant of F to 0.

For example, let C_t be the line whose x and y intercepts are t and 1−t, this is shown in the animation above. The equation of C_t is

${\frac {x}{t}}+{\frac {y}{1-t}}=1$

or, clearing fractions,

$x(1-t)+yt-t(1-t)=t^{2}+(-x+y-1)t+x=0.\,$

The equation of the envelope is then

$(-x+y-1)^{2}-4x=(x-y)^{2}-2(x+y)+1=0.\,$

Often when F is not a rational function of the parameter it may be reduced to this case by an appropriate substitution. For example if the family is given by C_θ with an equation of the form u(x, y)cosθ+v(x, y)sinθ=w(x, y), then putting t=e^iθ, cosθ=(t+1/t)/2, sinθ=(t-1/t)/2i changes the equation of the curve to

$u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t})=w$

or

$(u-iv)t^{2}-2wt+(u+iv)=0.\,$

The equation of the envelope is then given by setting the discriminant to 0:

$(u-iv)(u+iv)-w^{2}=0\,$

or

$u^{2}+v^{2}=w^{2}.\,$

其他定義

1. 包絡E₁係鄰近曲線C_t交點嘅極限。
2. 包絡E₂係一條同所有C_t相切嘅曲線。
3. 包絡E₃係由C_t所填充嘅區域嘅邊界。

於是乎，$E_{1}\subseteq {\mathcal {D}}$, $E_{2}\subseteq {\mathcal {D}}$同埋$E_{3}\subseteq {\mathcal {D}}$，其中${\mathcal {D}}$係由呢篇文開頭嘅定義所確定嘅曲線組成嘅集合。

例

例1

下面段文未譯好，歡迎你幫手。

These four definitions of the discriminant, E₁,E₂, and E₃, can lead to different sets. Consider for instance the curve y = x³ parametrised by γ : R → R² where γ(t) = (t,t³). The one-parameter family of curves will be given by the tangent lines to γ.

First we calculate the discriminant ${\mathcal {D}}$. The generating function is

$F(t,(x,y))=3t^{2}x-y-2t^{3}.$

Calculating the partial derivative F_t = 6t(x – t). It follows that either x = t or t = 0. First assume that x = t and t ≠ 0. Substituting into F: $F(t,(t,y))=t^{3}-y\,$ and so, assuming that t ≠ 0, it follows that F = F_t = 0 if and only if (x,y) = (t,t³). Next, assuming that t = 0 and substituting into F gives F(0,(x,y)) = −y. So, assuming t = 0, it follows that F = F_t = 0 if and only if y = 0. Thus the discriminant is the original curve and its tangent line at γ(0):

${\mathcal {D}}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\cup \{(x,y)\in \mathbb {R} ^{2}:y=0\}\ .$

Next we calculate E₁. One curve is given by F(t,(x,y)) = 0 and a nearby curve is given by F(t + ε,(x,y)) where ε is some very small number. The intersection point comes from looking at the limit of F(t,(x,y)) = F(t + ε,(x,y)) as ε tends to zero. Notice that F(t,(x,y)) = F(t + ε,(x,y)) if and only if

$L:=F(t,(x,y))-F(t+\varepsilon ,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.$

If t ≠ 0 then L has only a single factor of ε. Assuming that t ≠ 0 then the intersection is given by

$\lim _{\varepsilon \to 0}{\frac {1}{\varepsilon }}L=6t(t-x)\ .$

Since t ≠ 0 it follows that x = t. The y value is calculated by knowing that this point must lie on a tangent line to the original curve γ: that F(t,(x,y)) = 0. Substituting and solving gives y = t³. When t = 0, L is divisible by ε². Assuming that t = 0 then the intersection is given by

$\lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}}L=3x\ .$

It follows that x = 0, and knowing that F(t,(x,y)) = 0 gives y = 0. It follows that

$E_{1}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .$

Next we calculate E₂. The curve itself is the curve that is tangent to all of its own tangent lines. It follows that

$E_{2}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .$

Finally we calculate E₃. Every point in the plane has at least one tangent line to γ passing through it, and so region filled by the tangent lines is the whole plane. The boundary E₃ is therefore the empty set. Indeed, consider a point in the plane, say (x₀,y₀). This point lies on a tangent line if and only if there exists a t such that

$F(t,(x_{0},y_{0}))=3t^{2}x_{0}-y_{0}-2t^{3}=0\ .$

This is a cubic in t and as such has at least one real solution. It follows that at least one tangent line to γ must pass through any given point in the plane. If y > x³ and y > 0 then each point (x,y) has exactly one tangent line to γ passing through it. The same is true if y < x³ y < 0. If y < x³ and y > 0 then each point (x,y) has exactly three distinct tangent lines to γ passing through it. The same is true if y > x³ and y < 0. If y = x³ and y ≠ 0 then each point (x,y) has exactly two tangent lines to γ passing through it (this corresponds to the cubic having one ordinary root and one repeated root). The same is true if y ≠ x³ and y = 0. If y = x³ and x = 0, i.e., x = y = 0, then this point has a single tangent line to γ passing through it (this corresponds to the cubic having one real root of multiplicity 3). It follows that

$E_{3}=\varnothing .$

例2

In string art it is common to cross-connect two lines of equally spaced pins. What curve is formed?

For simplicity, set the pins on the x- and y-axes; a non-orthogonal layout is a rotation and scaling away. A general straight-line thread connects the two points (0, k−t) and (t, 0), where k is an arbitrary scaling constant, and the family of lines is generated by varying the parameter t. From simple geometry, the equation of this straight line is y = −(k − t)x/t + k − t. Rearranging and casting in the form F(x,y,t) = 0 gives:

$F(x,y,t)=t^{2}+t(y-x-k)+kx=0\,$

(1)

Now differentiate F(x,y,t) with respect to t and set the result equal to zero, to get

${\frac {\partial F(x,y,t)}{\partial t}}=2t+y-x-k=0\,$

(2)

These two equations jointly define the equation of the envelope. From (2) we have t = (−y + x + k)/2. Substituting this value of t into (1) and simplifying gives an equation for the envelope in terms of x and y only:

$x^{2}-2xy+y^{2}-2kx-2ky+k^{2}=0\,$

This is the familiar implicit conic section form, in this case a parabola. Parabolae remain parabolae under rotation and scaling; thus the string art forms a parabolic arc ("arc" since only a portion of the full parabola is produced). In this case an anticlockwise rotation through 45° gives the orthogonal parabolic equation y = x²/(k√2) + k/(2√2). Note that the final step of eliminating t may not always be possible to do analytically, depending on the form of F(x,y,t).

例3

Let I ⊂ R be an open interval and let γ : I → R² be a smooth plane curve parametrised by arc length. Consider the one-parameter family of normal lines to γ(I). A line is normal to γ at γ(t) if it passes through γ(t) and is perpendicular to the tangent vector to γ at γ(t). Let T denote the unit tangent vector to γ and let N denote the unit normal vector. Using a dot to denote the dot product, the generating family for the one-parameter family of normal lines is given by F : I × R² → R where

$F(t,{\mathbf {x} })=({\mathbf {x} }-\gamma (t))\cdot {\mathbf {T} }(t)\ .$

Clearly (x − γ)·T = 0 if and only if x − γ is perpendicular to T, or equivalently, if and only if x − γ is parallel to N, or equivalently, if and only if x = γ + λN for some λ ∈ R. It follows that

$L_{t_{0}}:=\{{\mathbf {x} }\in \mathbb {R} ^{2}:F(t_{0},{\mathbf {x} })=0\}$

is exactly the normal line to γ at γ(t₀). To find the discriminant of F we need to compute its partial derivative with respect to t:

${\frac {\partial F}{\partial t}}(t,{\mathbf {x} })=\kappa (t)({\mathbf {x} }-\gamma (t))\cdot {\mathbf {N} }(t)-1\ ,$

where κ is the plane curve curvature of γ. It has been seen that F = 0 if and only if x - γ = λN for some λ ∈ R. Assuming that F = 0 gives

${\frac {\partial F}{\partial t}}=\lambda \kappa (t)-1\ .$

Assuming that κ ≠ 0 it follows that λ = 1/κ and so

${\mathcal {D}}=\gamma (t)+{\frac {1}{\kappa (t)}}{\mathbf {N} }(t)\ .$

This is exactly the evolute of the curve γ.

例4

The following example generalizes the preceding one, and shows that in some cases the envelope of a family of curves may be seen as the topologic boundary of a union of sets, whose boundaries are the curves of the envelope. For $s>0$ and $t>0$ consider the (open) right triangle in a Cartesian plane with vertices $(0,0)$, $(s,0)$ and $(0,t)$

$T_{s,t}:=\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}<1\right\}.$

Fix an exponent $\alpha >0$, and consider the union of all the triangles $T_{s,t}$ subjected to the constraint $\textstyle s^{\alpha }+t^{\alpha }=1$, that is the open set

$\Delta _{\alpha }:=\bigcup _{s^{\alpha }+t^{\alpha }=1}T_{s,t}.$

To write a Cartesian representation for $\textstyle \Delta _{\alpha }$, start with any $\textstyle s>0$, $\textstyle t>0$ satisfying $\textstyle s^{\alpha }+t^{\alpha }=1$ and any $\textstyle (x,y)\in \mathbb {R} _{+}^{2}$. The Hölder inequality in $\textstyle \mathbb {R} ^{2}$ with respect to the conjugated exponents $p:=1+{\frac {1}{\alpha }}$ and $\textstyle q:={1+\alpha }$ gives:

$x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+t^{\alpha }{\Big )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}$,

with equality if and only if $\textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}$. In terms of a union of sets the latter inequality reads: the point $(x,y)\in \mathbb {R} _{+}^{2}$ belongs to the set $\textstyle \Delta _{\alpha }$, that is, it belongs to some $\textstyle T_{s,t}$ with $\textstyle s^{\alpha }+t^{\alpha }=1$, if and only if it satisfies

$x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}<1.$

Moreover, the boundary in $\mathbb {R} _{+}^{2}$ of the set $\textstyle \Delta _{\alpha }$ is the envelope of the corresponding family of line segments

$\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}=1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1$

(that is, the hypotenuses of the triangles), and has Cartesian equation

$x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}=1.$

Notice that, in particular, the value $\alpha =1$ gives the arc of parabola of the example 1, and the value $\alpha =2$ (meaning that all hypotenuses are unit length segments) gives the astroid.

Envelope of a family of surfaces

A one-parameter family of surfaces in three-dimensional Euclidean space is given by a set of equations

$F(x,y,z,a)=0$

depending on a real parameter a. For example the tangent planes to a surface along a curve in the surface form such a family.

Two surfaces corresponding to different values a and a' intersect in a common curve defined by

$F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\prime })-F(x,y,z,a) \over a^{\prime }-a}=0.$

In the limit as a' approaches a, this curve tends to a curve contained in the surface at a

$F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.$

This curve is called the characteristic of the family at a. As a varies the locus of these characteristic curves defines a surface called the envelope of the family of surfaces.

The envelope of a family of surfaces is tangent to each surface in the family along the characteristic curve in that surface.

概括

The idea of an envelope of a family of smooth submanifolds follows naturally. In general, if we have a family of submanifolds with codimension c then we need to have at least a c-parameter family of such submanifolds. For example: a one-parameter family of curves in three-space (c = 2) does not, generically, have an envelope.

應用

常微分方程

Envelopes are connected to the study of ordinary differential equations (ODEs), and in particular singular solutions of ODEs. Consider, for example, the one-parameter family of tangent lines to the parabola y = x². These are given by the generating family F(t,(x,y)) = t² – 2tx + y. The zero level set F(t₀,(x,y)) = 0 gives the equation of the tangent line to the parabola at the point (t₀,t₀²). The equation t² – 2tx + y = 0 can always be solved for y as a function of x and so, consider

$t^{2}-2tx+y(x)=0.\$

Differentiating and eliminating t gives the ODE

$\left({\frac {dy}{dx}}\right)^{2}\!\!-4x{\frac {dy}{dx}}+4y=0.$

Not surprisingly y = 2tx − t² are all solutions to this ODE. However, the envelope of this one-parameter family of lines, which is the parabola y = x², is also a solution to this ODE. Another famous example is Clairaut's equation.

偏微分方程

Envelopes can be used to construct more complicated solutions of first order partial differential equations (PDEs) from simpler ones. Let F(x,u,Du) = 0 be a first order PDE, where x is a variable with values in an open set Ω ⊂ Rⁿ, u is an unknown real-valued function, Du is the gradient of u, and F is a continuously differentiable function that is regular in Du. Suppose that u(x;a) is an m-parameter family of solutions: that is, for each fixed a ∈ A ⊂ R^m, u(x;a) is a solution of the differential equation. A new solution of the differential equation can be constructed by first solving (if possible)

$D_{a}u(x;a)=0\,$

for a = φ(x) as a function of x. The envelope of the family of functions {u(·,a)}_a∈A is defined by

$v(x)=u(x;\varphi (x)),\quad x\in \Omega ,$

and also solves the differential equation (provided that it exists as a continuously differentiable function).

Geometrically, the graph of v(x) is everywhere tangent to the graph of some member of the family u(x;a). Since the differential equation is first order, it only puts a condition on the tangent plane to the graph, so that any function everywhere tangent to a solution must also be a solution. The same idea underlies the solution of a first order equation as an integral of the Monge cone. The Monge cone is a cone field in the Rⁿ⁺¹ of the (x,u) variables cut out by the envelope of the tangent spaces to the first order PDE at each point. A solution of the PDE is then an envelope of the cone field.

In Riemannian geometry, if a smooth family of geodesics through a point P in a Riemannian manifold has an envelope, then P has a conjugate point where any geodesic of the family intersects the envelope. The same is true more generally in the calculus of variations: if a family of extremals to a functional through a given point P has an envelope, then a point where an extremal intersects the envelope is a conjugate point to P.

焦散曲線

内文：焦散曲線

Reflective caustic generated from a circle and parallel rays

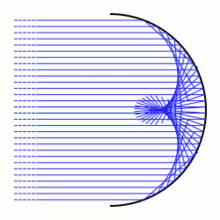
In geometrical optics, a caustic is the envelope of a family of light rays. In this picture there is an arc of a circle. The light rays (shown in blue) are coming from a source at infinity, and so arrive parallel. When they hit the circular arc the light rays are scattered in different directions according to the law of reflection. When a light ray hits the arc at a point the light will be reflected as though it had been reflected by the arc's tangent line at that point. The reflected light rays give a one-parameter family of lines in the plane. The envelope of these lines is the reflective caustic. A reflective caustic will generically consist of smooth points and ordinary cusp points.

From the point of view of the calculus of variations, Fermat's principle (in its modern form) implies that light rays are the extremals for the length functional

$L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt$

among smooth curves γ on [a,b] with fixed endpoints γ(a) and γ(b). The caustic determined by a given point P (in the image the point is at infinity) is the set of conjugate points to P.

惠更斯原理

Light may pass through anisotropic inhomogeneous media at different rates depending on the direction and starting position of a light ray. The boundary of the set of points to which light can travel from a given point q after a time t is known as the wave front after time t, denoted here by Φ_q(t). It consists of precisely the points that can be reached from q in time t by travelling at the speed of light. Huygens's principle asserts that the wave front set Φ_q0(s + t) is the envelope of the family of wave fronts Φ_q(s) for q ∈ Φ_q0(t). More generally, the point q₀ could be replaced by any curve, surface or closed set in space.

睇埋

• Ruled surface

出面網頁

• "Enveloppe d'une Famille de Courbes Planes" at Encyclopédie des Formes Mathématiques Remarquables