八點算法 (英文 :Eight-point algorithm 電腦視覺 演算法 ,攞來從一組對應嘅圖像點估計啲戥一副立體相機孖有拏褦嘅本質矩陣 (essential matrix)或者基礎矩陣 (fundamental matrix)嘅。個演算法係由Christopher Longuet-Higgins 喺1981年針對本質矩陣嘅情況引入嘅。理論上講,個演算法亦都喺基礎矩陣使得到,但實際上,Richard Hartley喺1997年描述嘅歸一化八點算法 啱種情況多啲。
個演算法名來源係從一組八粒(或者再多啲)對應嘅圖像點來估計本質矩陣或者基礎矩陣。之不過,演算法嘅變體可以採少過八粒點。
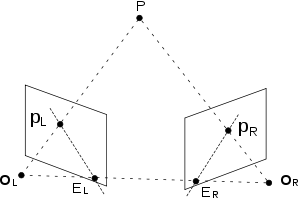
對極幾何示例。 兩台相機各自嘅投影點中心O L 同O R ,觀察緊點P。 P 喺每幅圖像平面上嘅投影表示成P L 同P R 。點E L 同E R 係對極點。兩台相機同空間裏頭一點嘅對極幾何 可以攞代數方程來表示(睇右圖)。簡單嚟講,兩粒相機點連成嘅線
O
L
O
R
¯
{\displaystyle {\overline {O_{L}O_{R}}}}
基線 」(英文 :baseline ),
O
L
P
¯
{\displaystyle {\overline {O_{L}P}}}
O
R
P
¯
{\displaystyle {\overline {O_{R}P}}}
對極線 」(英文 :epipolar lines )注意,無論點
P
{\displaystyle P}
O
L
P
¯
{\displaystyle {\overline {O_{L}P}}}
O
R
P
¯
{\displaystyle {\overline {O_{R}P}}}
O
R
O
L
¯
{\displaystyle {\overline {O_{R}O_{L}}}}
對極平面 」,英文 :epipolar plane )。參睇對極幾何相關內容 ,如果令
y
,
y
′
{\displaystyle y,y'}
P
{\displaystyle P}
y
′
T
E
y
=
0
{\displaystyle y'^{\mathrm {T} }\mathbf {E} y=0}
呢度描述有基本嘅八點算法,攞來估計本質矩陣
E
{\displaystyle \mathbf {E} }
齊次線性方程 ,其中個方程解戥
E
{\displaystyle \mathbf {E} }
估計理論 中嘅標準方法。
本質矩陣
E
{\displaystyle \mathbf {E} }
(
y
′
)
T
E
y
=
0
{\displaystyle (\mathbf {y} ')^{\mathrm {T} }\,\mathbf {E} \,\mathbf {y} =0}
約束到啲相應圖像點,喺條式裏便係攞歸一化圖像坐標迾
y
,
y
′
{\displaystyle \mathbf {y} ,\mathbf {y} '}
E
{\displaystyle \mathbf {E} }
E
{\displaystyle \mathbf {E} }
透過
y
=
(
y
1
y
2
1
)
{\displaystyle \mathbf {y} ={\begin{pmatrix}y_{1}\\y_{2}\\1\end{pmatrix}}}
y
′
=
(
y
1
′
y
2
′
1
)
{\displaystyle \mathbf {y} '={\begin{pmatrix}y'_{1}\\y'_{2}\\1\end{pmatrix}}}
E
=
(
e
11
e
12
e
13
e
21
e
22
e
23
e
31
e
32
e
33
)
{\displaystyle \mathbf {E} ={\begin{pmatrix}e_{11}&e_{12}&e_{13}\\e_{21}&e_{22}&e_{23}\\e_{31}&e_{32}&e_{33}\end{pmatrix}}}
約束亦都可以改寫成:
(
y
1
′
,
y
2
′
,
1
)
(
e
11
e
12
e
13
e
21
e
22
e
23
e
31
e
32
e
33
)
(
y
1
y
2
1
)
=
0
{\displaystyle (y'_{1},y'_{2},1){\begin{pmatrix}e_{11}&e_{12}&e_{13}\\e_{21}&e_{22}&e_{23}\\e_{31}&e_{32}&e_{33}\end{pmatrix}}{\begin{pmatrix}y_{1}\\y_{2}\\1\end{pmatrix}}=0}
y
1
′
y
1
e
11
+
y
1
′
y
2
e
12
+
y
1
′
e
13
+
y
2
′
y
1
e
21
+
y
2
′
y
2
e
22
+
y
2
′
e
23
+
y
1
e
31
+
y
2
e
32
+
e
33
=
0
{\displaystyle y'_{1}y_{1}e_{11}+y'_{1}y_{2}e_{12}+y'_{1}e_{13}+y'_{2}y_{1}e_{21}+y'_{2}y_{2}e_{22}+y'_{2}e_{23}+y_{1}e_{31}+y_{2}e_{32}+e_{33}=0\,}
或者
e
⋅
y
~
=
0
{\displaystyle \mathbf {e} \cdot {\tilde {\mathbf {y} }}=0}
其中有
y
~
=
(
y
1
′
y
1
y
1
′
y
2
y
1
′
y
2
′
y
1
y
2
′
y
2
y
2
′
y
1
y
2
1
)
{\displaystyle {\tilde {\mathbf {y} }}={\begin{pmatrix}y'_{1}y_{1}\\y'_{1}y_{2}\\y'_{1}\\y'_{2}y_{1}\\y'_{2}y_{2}\\y'_{2}\\y_{1}\\y_{2}\\1\end{pmatrix}}}
e
=
(
e
11
e
12
e
13
e
21
e
22
e
23
e
31
e
32
e
33
)
{\displaystyle \mathbf {e} ={\begin{pmatrix}e_{11}\\e_{12}\\e_{13}\\e_{21}\\e_{22}\\e_{23}\\e_{31}\\e_{32}\\e_{33}\end{pmatrix}}}
即係,
e
{\displaystyle \mathbf {e} }
y
~
{\displaystyle {\tilde {\mathbf {y} }}}
3
×
3
{\displaystyle 3\times 3}
y
′
y
T
{\displaystyle \mathbf {y} '\,\mathbf {y} ^{\mathrm {T} }}
每副對應嘅圖像點產生一枚向量
y
~
{\displaystyle {\tilde {\mathbf {y} }}}
P
k
{\displaystyle \mathbf {P} _{k}}
y
~
k
{\displaystyle {\tilde {\mathbf {y} }}_{k}}
e
{\displaystyle \mathbf {e} }
e
⋅
y
~
k
=
0
{\displaystyle \mathbf {e} \cdot {\tilde {\mathbf {y} }}_{k}=0}
畀定足夠多(至少八粒)線性無關嘅向量
y
~
k
{\displaystyle {\tilde {\mathbf {y} }}_{k}}
e
{\displaystyle \mathbf {e} }
y
~
k
{\displaystyle {\tilde {\mathbf {y} }}_{k}}
Y
{\displaystyle \mathbf {Y} }
e
T
Y
=
0
{\displaystyle \mathbf {e} ^{\mathrm {T} }\,\mathbf {Y} =\mathbf {0} }
個意思即係
e
{\displaystyle \mathbf {e} }
齊次線性方程嘅解 。
解呢條方程嘅標準方法意思即係
e
{\displaystyle \mathbf {e} }
Y
{\displaystyle \mathbf {Y} }
左奇異向量 對應於一個零奇異值 。假設至少有八粒線性無關向量
y
~
k
{\displaystyle {\tilde {\mathbf {y} }}_{k}}
Y
{\displaystyle \mathbf {Y} }
e
{\displaystyle \mathbf {e} }
E
{\displaystyle \mathbf {E} }
使用8個以上對應點來構建
Y
{\displaystyle \mathbf {Y} }
總體最細二乘問題 ;搵返
e
{\displaystyle \mathbf {e} }
‖
e
T
Y
‖
{\displaystyle \|\mathbf {e} ^{\mathrm {T} }\,\mathbf {Y} \|}
前提保證
‖
e
‖
=
1
{\displaystyle \|\mathbf {e} \|=1}
e
{\displaystyle \mathbf {e} }
Y
{\displaystyle \mathbf {Y} }
e
{\displaystyle \mathbf {e} }
3
×
3
{\displaystyle 3\times 3}
E
e
s
t
{\displaystyle \mathbf {E} _{\rm {est}}}
處理噪音圖像坐標嘅另一個後果係個結果矩陣可能唔滿足本質矩陣嘅內部約束,個約束即係佢啲奇異值當中有兩個係相等且非零、另一個為零。睇在唔同應用方面,戥內部約束偏差細啲或者大啲,成唔成問題都有可能。如果個估計得出嘅矩陣要滿足內部約束係好緊要,可以透過搵到rank 2
E
′
{\displaystyle \mathbf {E} '}
‖
E
′
−
E
e
s
t
‖
{\displaystyle \|\mathbf {E} '-\mathbf {E} _{\rm {est}}\|}
其中
E
e
s
t
{\displaystyle \mathbf {E} _{\rm {est}}}
Frobenius 矩陣範數 。呢個問題嘅解係幫
E
e
s
t
{\displaystyle \mathbf {E} _{\rm {est}}}
奇異值分解 先:
E
e
s
t
=
U
S
V
T
{\displaystyle \mathbf {E} _{\rm {est}}=\mathbf {U} \,\mathbf {S} \,\mathbf {V} ^{\mathrm {T} }}
其中
U
,
V
{\displaystyle \mathbf {U} ,\mathbf {V} }
S
{\displaystyle \mathbf {S} }
E
e
s
t
{\displaystyle \mathbf {E} _{\rm {est}}}
S
{\displaystyle \mathbf {S} }
S
′
=
(
s
1
0
0
0
s
2
0
0
0
0
)
,
{\displaystyle \mathbf {S} '={\begin{pmatrix}s_{1}&0&0\\0&s_{2}&0\\0&0&0\end{pmatrix}},}
其中
s
1
,
s
2
{\displaystyle s_{1},s_{2}}
S
{\displaystyle \mathbf {S} }
最後,
E
′
{\displaystyle \mathbf {E} '}
E
′
=
U
S
′
V
T
{\displaystyle \mathbf {E} '=\mathbf {U} \,\mathbf {S} '\,\mathbf {V} ^{\mathrm {T} }}
矩陣
E
′
{\displaystyle \mathbf {E} '}
基本嘅八點算法原則上亦都可以攞來估計返本質矩陣
F
{\displaystyle \mathbf {F} }
F
{\displaystyle \mathbf {F} }
(
y
′
)
T
F
y
=
0
{\displaystyle (\mathbf {y} ')^{\mathrm {T} }\,\mathbf {F} \,\mathbf {y} =0}
其中
y
,
y
′
{\displaystyle \mathbf {y} ,\mathbf {y} '}
Y
{\displaystyle \mathbf {Y} }
f
T
Y
=
0
{\displaystyle \mathbf {f} ^{\mathrm {T} }\,\mathbf {Y} =\mathbf {0} }
其中
f
{\displaystyle \mathbf {f} }
F
{\displaystyle \mathbf {F} }
F
{\displaystyle \mathbf {F} }
問題係噉樣產生嘅
Y
{\displaystyle \mathbf {Y} }
病態嘅 (ill-conditioned)。理論上,
Y
{\displaystyle \mathbf {Y} }
Y
{\displaystyle \mathbf {Y} }
Hartley 喺 1997 年嘅文章中解決唨呢個估計問題。佢對個問題嘅分析表明,個問題係由於均勻圖像坐標喺個空間
R
3
{\displaystyle \mathbb {R} ^{3}}
(
y
1
,
y
2
)
{\displaystyle (y_{1},y_{2})\,}
y
=
(
y
1
y
2
1
)
{\displaystyle \mathbf {y} ={\begin{pmatrix}y_{1}\\y_{2}\\1\end{pmatrix}}}
兩個
y
1
,
y
2
{\displaystyle y_{1},y_{2}\,}
y
{\displaystyle \mathbf {y} }
Y
{\displaystyle \mathbf {Y} }
(
700
,
700
)
±
(
100
,
100
)
{\displaystyle (700,700)\pm (100,100)\,}
y
{\displaystyle \mathbf {y} }
Y
{\displaystyle \mathbf {Y} }
作為呢個問題嘅解決方案,Hartley 提出應該根據以下原則,捉兩幅圖像中每幅圖像嘅坐標系獨立噉變換成新嘅坐標系。
新坐標系嘅原點應該以圖像點嘅質心(重心)為中心(有佢嘅原點)。呢個係透過捉原始來源翻譯成新來源來實現嘅。
平移後,坐標着統一縮放,令到從原點到一粒點嘅平均距離等於
2
{\displaystyle {\sqrt {2}}}
呢個原理通常會導致兩幅圖像嘅每一幅都有唔同嘅坐標變換。結果係新嘅均勻圖像坐標
y
¯
,
y
¯
′
{\displaystyle \mathbf {\bar {y}} ,\mathbf {\bar {y}} '}
y
¯
=
T
y
{\displaystyle \mathbf {\bar {y}} =\mathbf {T} \,\mathbf {y} }
y
¯
′
=
T
′
y
′
{\displaystyle \mathbf {\bar {y}} '=\mathbf {T} '\,\mathbf {y} '}
其中
T
,
T
′
{\displaystyle \mathbf {T} ,\mathbf {T} '}
基於本質矩陣嘅對極約束,而今可以重寫過,寫成:
0
=
(
y
¯
′
)
T
(
(
T
′
)
T
)
−
1
F
T
−
1
y
¯
=
(
y
¯
′
)
T
F
¯
y
¯
{\displaystyle 0=(\mathbf {\bar {y}} ')^{\mathrm {T} }\,((\mathbf {T} ')^{\mathrm {T} })^{-1}\,\mathbf {F} \,\mathbf {T} ^{-1}\,\mathbf {\bar {y}} =(\mathbf {\bar {y}} ')^{\mathrm {T} }\,\mathbf {\bar {F}} \,\mathbf {\bar {y}} }
其中
F
¯
=
(
(
T
′
)
T
)
−
1
F
T
−
1
{\displaystyle \mathbf {\bar {F}} =((\mathbf {T} ')^{\mathrm {T} })^{-1}\,\mathbf {F} \,\mathbf {T} ^{-1}}
y
¯
,
y
¯
′
{\displaystyle \mathbf {\bar {y}} ,\mathbf {\bar {y}} '}
F
¯
{\displaystyle \mathbf {\bar {F}} }
歸一化變換嘅目標係矩陣
Y
¯
{\displaystyle \mathbf {\bar {Y}} }
Y
{\displaystyle \mathbf {Y} }
f
{\displaystyle \mathbf {f} }
Y
{\displaystyle \mathbf {Y} }
f
¯
{\displaystyle \mathbf {\bar {f}} }
Y
¯
f
¯
{\displaystyle \mathbf {\bar {Y}} \,\mathbf {\bar {f}} }
f
¯
{\displaystyle \mathbf {\bar {f}} }
F
¯
{\displaystyle \mathbf {\bar {F}} }
F
{\displaystyle \mathbf {F} }
F
=
(
T
′
)
T
F
¯
T
{\displaystyle \mathbf {F} =(\mathbf {T} ')^{\mathrm {T} }\,\mathbf {\bar {F}} \,\mathbf {T} }
一般來講,本質矩陣嘅呢種估計好過非標準化坐標嘅估計。
每副點對都貢獻一個約束方程畀
E
{\displaystyle \mathbf {E} }
E
{\displaystyle \mathbf {E} }
E
{\displaystyle \mathbf {E} }
Kaveh Fathian 等提出唨五、六、七點算法,係透過直接計算旋轉四元數嚟規避唔去計算個本質矩陣
E
{\displaystyle \mathbf {E} }
[ 1] [ 2]
↑ Fathian, Kaveh (2018). "QuEst: A Quaternion-Based Approach for Camera Motion Estimation From Minimal Feature Points" . IEEE Robotics and Automation Letters . arXiv :1704.02672 doi :10.1109/LRA.2018.2792142 . ↑ Fathian, Kaveh (2018). "Camera relative pose estimation for visual servoing using quaternions" . Robotics and Autonomous Systems . doi :10.1016/j.robot.2018.05.014 .
Richard I. Hartley (June 1997). "In Defense of the Eight-Point Algorithm". IEEE Transactions on Pattern Recognition and Machine Intelligence . 19 (6): 580–593. doi :10.1109/34.601246 .