演算法

演算法可以喺有限嘅時間同記憶空間之內,透過形式語言(formal language;簡單講就係個個字都有精確定義嘅語言,相對於日常講嘢用嘅自然語言)嚟表達[1],用嚟計某一啲函數:噉講嘅意思係話,一串演算法會要求某啲特定嘅 input,跟住啲命令會描述一柞運算;當呢柞運算由人或者電腦執行嗰陣,會經過一連串數量有限嘅中介狀態[3],最後產生一個 output [4],並且喺呢個最終狀態嗰度終止執行。順帶一提,由一個中介狀態去到下一個嘅過程唔一定係決定性嘅,有好多演算法都涉及一啲帶有隨機性喺入面嘅運算[5][6]。
演算法嘅概念歷史悠久,有得一路追溯到去公元前嘅古希臘:由古希臘數學家諗出嚟嘅愛氏篩同埋係歐幾里得演算法等都可以算係早期演算法嘅例子;而演算法嘅英文名係由 9 世紀嘅波斯人數學家花剌子密(波斯文:محمد بن موسى الخوارزمي)個姓嗰度嚟嘅-佢個姓用羅馬字寫係 algoritmi,花剌子密佢做咗啲相關研究,局部噉確立咗演算法嘅概念;現代嘅演算法概念係喺 1928 年由德國數學家打域囂拔(David Hibert)喺佢嘗試解決可判定性嘅問題嗰陣奠定嘅。自從嗰陣開始,演算法同相關嘅研究就喺數學同電腦科學呢兩個領域嗰度俾人廣泛噉採用[7]。
定義
[編輯]
籠統噉講,「演算法」呢個詞嘅定義可以指「一串能夠精確噉定義一系列作業嘅規則」。呢個定義包含嗮所有嘅電腦程式-就連啲唔曉做數字上嘅運算嘅程式都包含喺呢個定義之內,而歐幾里得演算法同埋文頭嗰個流程圖所描述嘅都係符合呢個定義嘅演算法。演算法對於電腦處理數據嚟講係不可或缺嘅:電腦程式會包含一大柞嘅演算法,仔細噉教部電腦要做啲乜嘢運算同埋「以乜嘢次序做呢啲運算」,令部電腦曉解決用家想用嗰個程式解決嘅問題-呢啲問題可以包括咗計啲簡單嘅算術以至複雜嘅統計學作業等等都得[8][9]。
精確啲噉講,一段演算法包含一串作業,而串嘢要有以下呢啲特質[10][11]:
- 有某啲特定嘅次序;
- 唔具有歧義(ambiguity)嘅問題;
- 有得攞部理想嘅運算機械-即係有圖靈完整性(Turing completeness)嘅機械-嚟行;
- 曉自己結束運行-即係話可以係有限嘅時間之內行完,並且俾一個輸出出嚟睇,唔會有無限迴圈(infinite loop)嘅問題[12]。
集合論觀點
[編輯]演算法可以用集(set;睇埋集合論)嘅概念嚟想像。例如美國邏輯學家佐治·布勞斯(George Boolos)同佢嘅同事係噉樣描述「演算法」呢個概念嘅[13]:
| 「 | 原版英文:"No human being can write fast enough, or long enough, or small enough† [†"smaller and smaller without limit ... you'd be trying to write on molecules, on atoms, on electrons"] to list all members of an enumerably infinite set by writing out their names, one after another, in some notation. But humans can do something equally useful, in the case of certain enumerably infinite sets: They can give explicit instructions for determining the nth member of the set, for arbitrary finite n. Such instructions are to be given quite explicitly, in a form in which they could be followed by a computing machine, or by a human who is capable of carrying out only very elementary operations on symbols."
粵文翻譯:由於受到速度、時間同字體大細嘅限制,冇人能夠將一個雖然可以數但係無限大嘅集入面所包含嘅物件用任何嘅某種寫法寫嗮出嚟。但係,對住某啲嘅呢種可數但係無限大嘅集,人能夠做一啲同等有用嘅嘢(指演算法):佢哋可以俾一啲明確嘅指示出嚟,去搵出個集所包含嘅第 n 件物件,而 n 係指是但一個細過無限大嘅整數。呢啲指示都要充分明確至得,而且形式上要可以令到一個曉計數嘅機器(電腦)⸺或者一個人,不過呢個人只要曉得好簡單咁處理符號就得嘞⸺能夠跟從呢啲指示。 |
」 |
上面呢段嘢當中所講嘅「可數嘅無限集」係數學上嘅一個概念,指一個包含咗多樣嘢嘅集,而呢個集包含嘅物件有無限咁多件,但啲件數可以用由 1 開始嘅整數嚟數。所以貝勞斯同佢啲同事講緊就係話:一串演算法係一連串指令,例如係一柞好似「; 代表輸出(output), 同 代表輸入(input)」噉嘅算式;而呢柞指令能夠由是但一啲輸入嗰度計同整一啲輸出出嚟俾人睇,而且呢啲輸入-至少喺理論上-係幾大都得嘅(但實際上因為人有嘅電腦嘅運算能力有限,所以對於輸入嘅大細梗會有個上限)[14][15]。
表達
[編輯]
想像家陣有一部曉跟事先指定咗嘅規則嚟由輸入計輸出嘅機械,呢部機械嘅記憶體係無限咁多嘅-即係一部理想化嘅圖靈機(Turing machine)[16][17]。呢部機械計緊嘅運算嘅內容可以用多種唔同嘅圖表同語言表達,包括係自然語言、虛擬碼(pseudocode)、流程圖、狀態轉移表同埋係多種嘅程式語言呀噉。用自然語言-即係好似廣東話等日常講嘢用嘅語言-寫嘅符號(虛擬碼)對一般人嚟講易明,但就好多時都會有歧義嘅問題,而且電腦唔會識睇。程式語言(programming language)係專門為咗俾人用嚟同電腦溝通而設嘅特殊語言,電腦會睇得明,所以演算法好多時都會用程式語言嚟定義[18]。
舉個簡單例子說明,好似係以下呢段用粵文寫嘅演算法噉,就做咗一連串嘅運算[18]:
- 要解決嘅問題:家吓俾一列正數(輸入)你,假設呢個列唔係一個空列,同我搵嗰列數入面最大嗰個出嚟。
- 用粵文寫嘅演算法嘅步驟:
- 設一個變數,叫佢做「max」,並且將佢個數值設做「0」;
- 將收到嗰列正數逐個逐個攞嚟同 max 比較吓;
- 如果撞到一個大過 max 嘅數(叫呢個數做「x」)嘅話,將 max 嘅數值設做 x,並且繼續將 max 同下個正數比較吓;(邏輯代數)
- 將最後得出嗰個 max 嘅數值俾出嚟(輸出)。max 嘅數值會係成列數入面最大嗰個。
呢串演算法用 Python(1991 年出嘅一種程式語言)寫出嚟嘅話會係[18]:
# Input:一列冧巴,叫列冧巴做「L」。
# Output:L 入面最大嘅冧巴。
def find_max (L):
max = 0 # 設最大值做 0。
for x in L: # 同 L 入面每個元件做以下嘅嘢...
if x > max: # 如果 x 大過最大值...
max = x # ... 設最大值做 x。
return max # 做完嗮上述嘅嘢後,俾返個最大值出嚟。
諗演算法嘅過程係將一個作業揼散做組成佢嘅細部份,而每個細部份都要係一啲電腦普遍都會識做嘅簡單工作(例如係「比較兩個數,睇吓邊個大啲」)-呢啲細部份可以話係組成演算法嘅元素,有咗佢哋就能夠將任何「人類會想用電腦做嘅工作」砌出嚟[18]。
三大層次
[編輯]演算法嘅表達方法大致上可以分做三大圖靈機描述層次[19]:
- 高層描述(high-level description):會描述一串演算法要做乜嘢運算,但就忽略點樣將串演算法實行落去部運算機械嗰度。一般人會睇得明,但運算機械唔會[註 1]。可以睇埋高階程式語言同虛擬碼。
- 實行性描述(implementation description):會話俾一部圖靈機知要點樣郁同要點樣將啲數據儲喺啲數據庫嗰度。喺呢個層次仲未會話到運算過程嗰啲中介狀態同埋函數嘅詳情俾人知。
- 形式描述(formal description):最仔細,會講明埋運算過程嗰啲中介狀態同函數。
上面嗰段 Python 碼屬於高層嘅描述-就算睇咗佢,一個人仲係唔會知道部電腦嗰啲邏輯門(logic gate)做咗乜嘢運算。舉個簡單嘅例子說明,一部廿一世紀初嘅電子電腦喺計加數嗰陣係用類似以下噉嘅機制做嘅:想像家吓個工程師手上有一柞邏輯門,邏輯門係一種電子元件,唔同種類嘅邏輯門有唔同嘅輸入輸出關係,喺收到某啲特定嘅「0」(冇電)同「1」(有電)訊號嗰陣會俾出「0」(冇電)或者「1」(有電)訊號做輸出;例如:
- 一個簡單嘅異或門(XOR gate)會收兩個輸入,如果兩個輸入值一樣,個門會俾「0」,如果兩個輸入值唔同,個門會俾「1」(A XOR B);
- 一個簡單嘅與門(AND gate)會收兩個輸入,只有當兩個輸入都係「1」嗰陣,個門先會俾「1」(A AND B);
然後有咗呢啲元件,一個工程師可以整出以下嘅半加法器集成電路[20]:

呢個電路嘅真值表如下:
輸入 輸出 A B C S 0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0
用日常講,當 A 同 B 呢兩個輸入都係「0」嗰陣,輸出會係「00」(兩個輸出都冇電);當 A 同 B 是但一個係「1」另一個係「0」嗰陣,輸出會係「01」(得 S 有電);最後,如果兩個輸入都係「1」,噉個輸出會係「10」(得 C 有電)。如果用二進制睇嘅話,上述呢個電路做得到 嘅簡單運算:當兩個輸入都係「0」,,當得其中一個輸入係「1」,,而當兩個輸入都係「1」嗰陣時,,當中「10」喺二進制入面相當於十進制嘅「2」[21]。上述嘅過程如果用 Python 同 C++ 等嘅高階程式語言寫嘅話,會類似噉:
a = 1 + 1;
就算睇咗呢段碼,用家都完全唔會知道邏輯門做咗嘅嘢[19]。
出名演算法
[編輯]搜尋演算法
[編輯]
搜尋演算法(search algorithm)泛指用嚟由數據結構當中搵出想要嗰件數據嘅演算法-輸入係「數據結構」同「想要嗰件數據嘅樣」,而輸出係「想要嗰件數據喺數據結構當中嘅邊個位」。廿一世紀嘅電腦科學界有多種搜尋演算法可以用,而每種都有優缺點[22]。
窮舉搜尋
[編輯]窮舉搜尋(brute-force search)係最原始嗰種搜尋演算法,指將手上嘅數據(事先以某啲方式排好咗)逐個逐個耖,一路耖到搵到想要嗰個為止。例如手上有一列以隨機次序排嘅數字,用家想要由呢個數列當中最大嗰個出嚟,用窮舉搜尋嘅話,睇嗰個人就要睇嗮個數列當中嘅每個數字,再俾出最大嗰個出嚟;呢段簡單嘅演算法用粵文寫出嚟嘅話會係[23]:
- 如果個列入面冇數字,噉就唔會有「最大嗰個數」。
- 先假定個列入面第一個數字係最大嗰個。
- 逐個逐個噉去睇個列入面啲數字,如果撞到個數字大過而家手上嗰個「最大數字」嘅話,將新撞到呢個數字設做「最大數字」。
- 如果睇勻嗮個列入面啲數字嘅話,將手上嗰個「最大數字」交出嚟做答案。
上述呢串演算法用比較形式些少嘅虛擬碼寫出嚟嘅話會係噉:
// Input: A list of numbers L.
// Output: The largest number in the list L.
if L.size = 0 return null;
largest ← L[0];
for each item in L, do
if item > largest, then
largest ← item;
return largest;
// 當中 "←" 代表指定敘述-「A ← B」即係將 A 嘅數值設做 B;
// 而 "return X" 會終止串演算法,並且將 X 嘅數值攞嚟做輸出。
廿一世紀嘅研究者一般都會嫌呢串演算法唔夠好,原因係呢串演算法喺最壞情況(worst-case)嗰陣要睇嗮成個列先至搞得掂,所以又有人諗咗第啲演算法出嚟做呢樣工作-而呢啲新演算法好多時都曉淨係睇個數字列嘅一小部份就經已搵得出想要嗰個數字[22]。
對分檢索
[編輯]對分檢索(binary search)係用嚟由一個預先排好咗次序(睇下面排序演算法)嘅數列嗰度搵某一個特定數字出嚟嘅演算法。對分檢索嘅做法係首先將行資料拆做兩橛,再睇吓中間嗰個數係咪等如要搵嗰個數(目標),假如個數列係預先由細到大排好咗嘅話,噉就意味一樣嘢:如果數列中間嗰個數大過個目標,噉個目標實係喺中間個數前面,而如果數列中間嗰個數細過個目標,噉個目標實係喺中間個數後面,跟手段演算法就可以再重複呢個程序,將個搜索範圍縮細,最後搵到個目標嘅數字(假如個目標真係存在喺嗰行數列入面嘅話)。好似係以下呢段虛擬碼噉[24][25]:
function binary_search(A, n, T):
L := 0 // 設個數做「左邊界」
R := n − 1 // 設個數做「右邊界」
while L <= R:
m := floor((L + R) / 2) // 將由 L 至 R 嗰段嘢砍兩橛,m 設做中間位
if A[m] < T: // 如果第 m 個數細過目標(T)嘅話,即係話個目標應該喺第 m 個數後面。
L := m + 1
else if A[m] > T: // 如果第 m 個數細過目標(T)嘅話,即係話個目標應該喺第 m 個數前面。
R := m - 1
else:
return m // 如果第 m 個數等如目標嘅話,就將嗰個數做輸出。
return unsuccessful

對分檢索平均會快過「吓吓都將數列入面嘅數逐個逐個睇一次」嘅窮舉搜尋:喺最壞情況下,想搵嗰個數會係個數列嘅第一個或者最尾嗰個,而喺呢個情況下,用對分檢索嚟做搜尋要做 咁多次比較(當中 係「個數列入面有幾多個數字」),而「吓吓將數列入面逐個逐個睇一次」喺最壞情況之下就要做 次比較, 數值永遠細過 [註 2]。「由一個數列當中搵一個特定數字出嚟」係電腦好常要做嘅基本作業,如果(例如)喺一個程式當中部電腦要做呢個作業 100 次嘅話,噉一個用對分檢索嘅程式基本上實會快一截,所以編程員多數會比較鍾意用對分檢索[24]。
排序演算法
[編輯]
排序演算法(sorting algorithm)泛指用嚟將一柞物件以某啲特定次序(例如由數值細到大)排好嘅演算法。呢種演算法嘅價值在於支援第啲演算法-有唔少演算法都係要啲數據事先排好咗先至會啱用,例子有頭先提到嘅對分檢索[22][26]。
快速排序
[編輯]快速排序(quicksort)係指用嚟將一個數列入面啲數字由細至大排好嘅演算法-輸入係一個(亂糟糟嘅)數列,而輸出係執好咗嘅數列[27][28]。步驟如下:
- 喺個數列入面是但揀個數字,設佢做基準(pivot)。
- 重新排序數列:將個數字重新排過,數值上細過個基準嘅數字冚唪唥搬去個基準前面,而數值上大過個基準嘅數字就冚唪唥搬嗮去個基準後面;做咗呢個步驟之後,個基準會喺正佢嘅最終位置。
- 將個數列斬做兩橛-「細過個基準嗰柞數字」同埋「大過個基準嗰柞數字」,並且分別噉對嗰兩橛做上述嗰兩個步驟。
呢串演算法俾人好廣泛噉攞嚟將啲數列嘅次序排好。上述呢串演算法用 Python 寫出嚟嘅話會係噉嘅[29]:
def sort(array=[12,4,5,6,7,3,1,15]): # 定義一個子程序,array 係要處理嗰個數列。
less = []
equal = []
greater = [] # 設三個陣列。
if len(array) > 1:
pivot = array[0] # 揀最頭個數做 pivot。
for x in array: # 將 array 當中每一個數 x...
if x < pivot: # 如果 x < pivot... 將 x 加落去 less 呢個陣列嗰度。
less.append(x)
if x == pivot: # 如果 x = pivot... 將 x 加落去 equal 呢個陣列嗰度。
equal.append(x)
if x > pivot: # 如果 x > pivot... 將 x 加落去 greater 呢個陣列嗰度。
greater.append(x)
return sort(less)+equal+sort(greater) # 喺 Python 入面,「+」可以代表「將兩個陣列拼埋一齊」;將 less、equal 同 greater 砌埋一齊做輸出。
else:
return array
# 個子程序會以 less 同 greater 做輸入再行過,行若干次,行到輸入嘅長度係 0 為止。
冒泡排序
[編輯]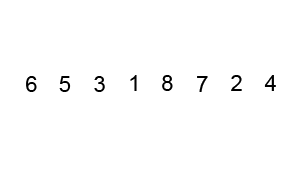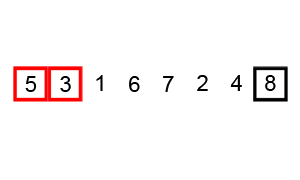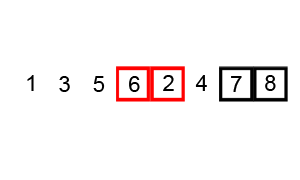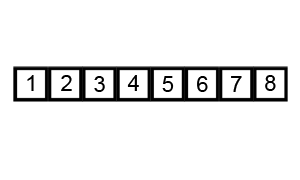
冒泡排序(bubble sort / sinking sort)係一種用嚟將一個數列入面啲數字由細至大排好嘅演算法,做法係喺每一步攞相鄰嘅兩個數比較,將兩個數由細到大排好,再將個過程做若干次,做到成個數列都排好嗮為止。原則上,冒泡排序並唔好用-喺最壞情況下要行成 咁多步先行得完,所以喺現實,冒泡排序多數都淨係俾人用嚟做教育用途[30][31]。
例如如果用冒泡排序同 5, 1, 4, 2, 8 呢個數列排序嘅話:
- 第一回合
- ( 5 1 4 2 8 ) → ( 1 5 4 2 8 ),5 > 1,所以將 5 同 1 位置互換,
- ( 1 5 4 2 8 ) → ( 1 4 5 2 8 ),5 > 4,所以將 5 同 4 位置互換,
- ( 1 4 5 2 8 ) → ( 1 4 2 5 8 ),5 > 2,所以將 5 同 2 位置互換,
- ( 1 4 2 5 8 ) → ( 1 4 2 5 8 ),5 < 8,所以 5 同 8 唔使郁。
- 第二回合
- ( 1 4 2 5 8 ) → ( 1 4 2 5 8 )
- ( 1 4 2 5 8 ) → ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) → ( 1 2 4 5 8 ),查實到咗呢一步,個數列經已排好咗,但段演算法要再重新睇多次個數列先至知呢一點。
- 第三回合
- ( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
- ( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
歐幾里得演算法
[編輯]
1599 = 650 × 2 + 299
650 = 299 × 2 + 52
299 = 52 × 5 + 39
52 = 39 × 1 + 13
39 = 13 × 3 + 0
歐幾里得演算法(Euclid's algorithm),係用嚟求最大公因數嘅一串演算法,首次記載係喺大約公元前 300 年嘅古希臘數學家歐幾里得嗰本《幾何原本》(英文:Elements)入面[32][33]。歐幾里得佢係噉樣講嘅:(粵文翻譯)「家吓有兩個彼此唔係對方因數嘅數,個問題係要搵出佢哋嘅最大公因數」,佢首先諗到一點-要計佢哋最大公因數嗰兩個數相減嘅話,得出嗰個數一定係個最大公因數嘅倍數。佢諗出嗰串演算法步驟簡單講如下[34]:
- 要搵佢哋最大公因數當中,大啲嗰個設做 ,細啲嗰個設做 ;
- 將 乘大佢,睇吓要乘幾先會變到大過 ,即係話 -喺呢條算式入面, 會係一個正整數,而 係一個餘數;
- 睇吓 係唔係等如零;
- 如果係嘅話, 就係要搵嗰個最大公因數;
- 如果唔係嘅話,將 同 當中大啲嗰個設做 ,細啲嗰個設做 ;
- 跳返去步驟 2。
要將呢串演算法用電腦嚟執行嘅話好簡單,淨係需要幾個種類嘅指令已經夠:條件性嘅 GOTO、無條件性嘅 GOTO、設變數同埋基本嘅算術[35]。
- 實現例子 1

以下呢段碼係歐幾里得演算法嘅一個可能實現形式(雖然實際上係一個唔多靚嘅演算法)。佢個做法嘅基本原理係將要搵佢哋最大公因數嗰兩個數設做 (大啲嗰個)同 (細啲嗰個)兩個變數,再將 由 嗰度減出嚟,減到得出個數細過 為止[36]。
輸入:
1 [設兩個變數-L 同 S,並且將佢哋嘅數值設做 同埋 嘅] INPUT L, S 2 [將 初始化:將個餘數嘅值設做等如 嘅] R ← L
E0:確保 。
3 [確保 真係細過 ] IF R > S THEN 真係細過 ,所以唔使做 #4、#5、同 #6 呢幾個交換步驟: GOTO step #6 ELSE 唔係細過 ,所以要做交換步驟嚟將兩個數掉轉: 4 L ← R 5 R ← S 6 S ← L
E1:搵個餘數出嚟-將 由 減出嚟,減到得出嘅餘數 細過 為止。
7 IF S > R THEN
GOTO 10
ELSE
8 R ← R − S
9 GOTO 7
E2:個餘數係咪零?如果係嘅話,個程式終止得,如果唔係嘅話,串演算法要再行落去,直至得出一個係零嘅餘數。
10 IF R = 0 THEN
GOTO 15
ELSE
CONTINUE TO 11
E3:將 同 對調,用 嚟做啲數字嘅中轉站。
11 L ← R
12 R ← S
13 S ← L
14 [重複上面嘅程序]
GOTO 7
輸出:
15 [將個答案顯示出嚟俾解緊難嗰個人睇]
PRINT S
搞掂:
16 HALT, END, STOP.
- 實現例子 2
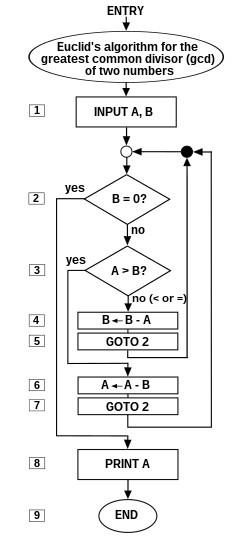
以下呢個係歐幾里得演算法嘅第個實現例子。佢淨係使用咗 6 個核心指令,相對於第一個例子嘅 13 個,俾好多人覺得係一個「靚」啲嘅演算法-因為學界一般都認為,所謂嘅「elegant」係指「用最少嘅指令類做最多嘅嘢」。佢用嗰種程式語言係以「LET [] = []」嚟設變數嘅數值嘅。
5 REM Euclid's algorithm for greatest common divisor
6 PRINT "唔該打兩個大過 0 嘅整數"
10 INPUT A,B
20 IF B = 0 THEN GOTO 80
30 IF A > B THEN GOTO 60
40 LET B = B - A
50 GOTO 20
60 LET A = A - B
70 GOTO 20
80 PRINT A
90 END
如果用緊嘅程式語言係比較物件導向嘅話,可以用 Java 程式語言 噉做:
// Euclid's algorithm for greatest common divisor
integer euclidAlgorithm (int A, int B){
A = Math.abs(A);
B = Math.abs(B);
while (B != 0){
if (A > B) A = A - B;
else B = B - A;
}
return A;
}
以上嘅呢啲演算法由相關領域嘅研究者用好多唔同嘅數字輸入試過,證實咗係掂嘅,亦都有數學家用數學歸納法(mathematical induction)嘅方法證明咗佢真係行得通嘅[37][38]。
搵路演算法
[編輯]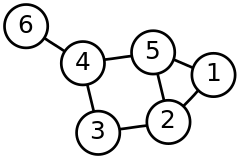
搵路演算法(pathfinding algorithm)係人工智能(AI)上嘅一個大課題,指教一個 AI 喺空間入面指定兩個點,並且搵出一條連接兩點嘅線。做搵路嘅演算法有好多用途,例如喺機械人學上教機械人探索自己周圍嘅空間,以及喺遊戲製作上教遊戲 AI 喺遊戲空間入面搵出要行嘅路線[39][40]。
一般嚟講,搵路演算法-無論係咪電子遊戲用嘅都好-都會[41][42]
- 攞一幅圖做輸入
input:呢類演算法通常唔能夠直接處理一個環境,而係要靠第串演算法,simplify,將個環境變成一幅圖(graph);圖論(graph theory)當中嘅一幅圖會有若干個節點(node),並且指明邊啲節點之間有連結,喺應用上,一個可能嘅做法係個輸入最先嗰個數字代表節點嘅數量,跟住嘅數字表示邊啲節點之間有連結(睇埋陣列),例如[6, 1-2, 1-5, 2-5, 2-3, 5-4, 3-4, 4-6]表示幅圖有 6 個節點,節點 1 同節點 2 之間有連結(可以由節點 1 行去節點 2 或者相反)、節點 1 同節點 5 之間有連結(可以由節點 1 行去節點 5 或者相反)... 如此類推;simplify要做嘅嘢係攞要探索嗰個環境做輸入,輸出一個表示個環境當中有邊啲重要位置(節點)同邊啲位置之間有路能夠互通(連結)嘅圖,等搵路演算法做嘅嘢容易啲[41]。 - 喺電子遊戲入面用嘅搵路演算法通常會用權重表(weighted graph),意思即係話個表每條連結都會有個數值[註 3],表示嗰條路線嘅成本(cost)[43]:例如有一個
simplify演算法會每條路都俾個權重值佢,個數值愈大表示條路愈難行(成本高);想像其中兩個節點之間有兩條可能路線a同b,a係一條完全冇機關嘅平路,而b長過a之餘仲有十個陷阱設咗喺度,噉正路嚟講,假設a同b喺其他因素上完全相等,b嘅權重值理應會大過a嘅[44]。 - 最後串演算法會俾一條路線嚟做輸出
output[45]。
有關搵路演算法嘅具體實現,可以睇吓迪卡斯特拉演算法同埋 A* 搜尋演算法。

模擬牛頓定律
[編輯]1 冇任何物理法則。
2 有重力,但冇碰撞探測。
3 有重力同碰撞探測,但冇剛體動力學。
4 有齊所有基本嘢。
遊戲物理(game physics)係指喺設計一個電子遊戲嗰陣將物理定律用電腦程式嘅形式表達出嚟,等部電腦識得真實噉模擬現實世界嘅物理俾啲玩家睇,令到啲玩家能夠覺得個遊戲有返咁上下真實度,並且投入去隻遊戲裏面-喺廿一世紀,大部份嘅電子遊戲都要做呢樣嘢,得少數嘅例外(例如一隻模擬捉象棋嘅電子遊戲)可以唔使模擬物理定律。一般嚟講,遊戲嘅物理都唔會完全跟足現實嘅物理嘅-好多時淨係會求有足夠嘅真實度[46][47]。
以下呢段用 C 程式語言寫嘅源碼可以攞嚟模擬喺牛頓第二定律(Newton's second law)之下郁動嘅物體[46]:
double t = 0.0;
float dt = 1.0f;
float velocity = 0.0f;
float position = 0.0f;
float force = 10.0f;
float mass = 1.0f;
// 設一大柞變數,包括咗時間點(t)、時間間隔(dt)、速度(velocity)、位置(position)、件物體受嘅力(force)、同件物體嘅質量(mass)。
while ( t <= 10.0 ) // 重複噉計若干次,計到時間點係 10 為止。
{
position = position + velocity * dt;
velocity = velocity + ( force / mass ) * dt; // 用牛頓第二定律計吓件物體受嘅力同佢嘅質量會點影響佢嘅速度。
t += dt;
}
呢段嘢會俾嘅輸出如下,個程式列嗮佢模擬嗰件物體喺每個時間點 嘅位置同速度出嚟[46]:
t=0: position = 0 velocity = 0
t=1: position = 0 velocity = 10
t=2: position = 10 velocity = 20
t=3: position = 30 velocity = 30
t=4: position = 60 velocity = 40
t=5: position = 100 velocity = 50
t=6: position = 150 velocity = 60
t=7: position = 210 velocity = 70
t=8: position = 280 velocity = 80
t=9: position = 360 velocity = 90
t=10: position = 450 velocity = 100
分類準則
[編輯]要將演算法分類,可以用好多唔同嘅準則:
有冇遞歸
[編輯]遞歸(recursion)係好多演算法有嘅特性,(簡化噉講)指串演算法當中有個子程式會用到佢自己,例如以下呢段簡單嘅碼噉[48][49]:
function dream()
print "Dreaming"
dream() // dream 呢個子程式當中用到自己。
喺編程上,遞歸可以用嚟解決一啲可以揼散做一大柞細問題嘅問題,而且當中每一個細問題都屬同一個類型,例如歐幾里得嘅演算法可以用 C 程式語言寫成以下嘅遞歸程式[48]:
int gcd(int A, int B) { /* gcd 係一個子程式,攞 A 同 B 兩個數做 input */
if (B == 0) /* 如果 B = 0... */
return A; /* ... 俾 A 做輸出 */
else if (A > B)
return gcd(A-B,B); /* 用 (A-B) 同 B 做輸入,行多次 gcd */
else
return gcd(A,B-A); /* ... */
好出名嘅河內塔(Tower of Hanoi)問題可以用遞歸演算法輕鬆解決[50]。
係咪決定性
[編輯]
決定性演算法(deterministic algorithm)係指本質上決定性嘅演算法,而非決定性演算法(non-deterministic algorithm)係指冇呢種特徵嘅演算法:決定性演算法喺每個步驟由輸入去輸出都好精確,冇任何隨機性喺入面,俾同一個輸入串演算法實會出同一個輸出[註 5][51];而非決定性演算法就相反,會有隨機性喺入面,所以就算吓吓俾同一樣嘅輸入佢,出嗰個輸出都可能會唔同咗,可以睇吓擬亂數產生[52]。
例:RPG 遊戲當中成日會有一大柞招式俾角色用,一個招式有若干個屬性,包括咗嗰招嘅殺傷力同命中率等等,當一個角色用一個命中率係 80% 嘅招式嗰陣,一個常見做法係遊戲程式內部會用 RNG 產生一個 0 至 1 之間嘅數字,而如果個數字大過或者等如 0.8,噉嗰吓攻擊就會打中,否則就會唔中,實際例子有寵物小精靈系列[53]。
決定性同非決定性演算法各有優劣-非決定性演算法嘅輸出難以預測,喺睇個輸出之前,一個非決定性演算法嘅輸出會以一個概率分佈(probability distribution)嘅形式存在,而非決定性演算法「輸出缺乏精確性」呢一點表示好多要求高度精確嘅科學同工程學應用唔能夠用呢啲演算法,但非決定性演算法「難以預測」呢一個特性又有第啲用途,例如,例如係一個模擬啤牌嘅遊戲程式喺洗牌嗰陣,就需要用到非決定性演算法,因為啤牌遊戲一般都預咗玩家冇能力預測抽到嘅牌係乜樣嘅[54],而統計學同機械學習嘅應用上都會用到非決定性演算法[55]。
係咪近似性
[編輯]近似演算法(approximation algorithm)係指嘗試搵出近似想要嘅答案嘅數值嘅演算法,而精準演算法(exact algorithm)係指要求搵到嘅答案同目標完全一樣:演算法一般都會俾出(通常係以數字形式存在嘅)答案,精準演算法要求個輸出同目標答案完全一樣,而近似演算法淨係要求個輸出同目標答案相近;例如喺 RPG 遊戲當中計一吓攻擊中唔中-1 代表「中」、0 代表「唔中」-就係一個精準演算法,要求個答案同目標數值完全一樣,但喺好多統計學同機械學習上嘅應用當中,可能輸出嘅數量極大-原則上如果答案嘅數值係連續性(continuous;可以小數點後有幾多個位都得),答案嘅可能數值會有無限咁多個,所以喺呢種情況下,串演算法只會務求俾出一個「理應會接近真實答案」嘅數值做輸出。即係話一個近似演算法會答嘅唔係「答案係幾多」而係「答案相信係喺幾多同幾多之間」或者「真正答案應該會接近呢個數值」[56][57]。

爬山演算法(hill climbing algorithm)係機械學習上一種常用嚟做最佳化(optimization;指研究點樣喺特定情況下將一個函數或者變數最大化或者最小化)嘅近似演算法;想像一個數學模型,有兩個參數, 同 ,而家用指標 嚟衡量個模型有幾「好」,而 係數值愈細代表個模型愈理想嘅[註 6]。家陣 同 經已有咗數值,所以個模型喺上圖入面有個座標位置,而個爬山演算法可以喺每一步噉做:
- 加減 同 嘅數值嚟改變個模型,即係個模型有 4()個前進方向;
- 計四個數值 ,當中 係移去第 個方向會得到嘅 值;
- 按「揀 值最小化嘅方向」呢條法則嚟改變 同 嘅數值;
- 重複,直至結束條件達到為止。
如果順利,個模型嘅 值會慢慢變到愈嚟愈細(接近理想數值),不過原則上,呢個最後嘅答案值唔保證會係理想數值-可能喺睇到嘅空間外有更低嘅可能 值,但呢串演算法唔會能夠保證將個模型帶到去嗰個數值-所以係一個近似演算法[58]。
按點樣處理複雜性
[編輯]窮舉演算法
[編輯]窮舉演算法(brute-force algorithm)指嘅係一啲「試嗮所有可能答案,再揀最好嗰個出嚟」嘅演算法[59],例如如果要由一個數列當中搵某一個特定嘅數字出嚟,可以用一個窮舉嘅方法:將個數列入面嗰啲數字逐個逐個攞嚟睇,睇吓嗰個數字係咪想要嗰個,最後俾個輸出。呢種做法喺個數列(例如)得三個數字嗰陣唔會有乜問題,但喺現實應用上,要耖嘅數列好多時都閒閒地有成幾千個數字,而喺(例如)教人工智能捉象棋嘅情況下,一盤象棋會有成上萬個可能情況,用窮舉演算法會嘥好多時間精神,實證嘅研究亦都表明咗窮舉演算法根本行唔通[60]。
相比之下,好似正話提到嘅對分檢索方法就唔係一個窮舉演算法,因為呢串演算法唔會將所有可能嘅答案冚唪唥都睇一次;而廿一世紀嘅電腦科學界同相關領域喺解起問題上嚟都唔會用窮舉演算法,而係好多時會集中思考點樣由成千上萬個可能性當中揀一部份出嚟處理[61][62]。可以睇吓近似演算法同蒙地卡羅樹搜索。

分治演算法
[編輯]
分治演算法(divide-and-conquer algorithm)係指重複係噉將手上要解嗰個問題砍件做一柞細啲(而且一個板)嘅問題,直至每一份細問題都有返咁上下簡單為止,即係話[63][64]:
例如合併排序(merge sort)就係分治演算法嘅一種-合併排序係一種(喺某啲情況下好用嘅)排序演算法,會將要排好嘅數據列砍件做細細橛,將每一橛排好咗之後就可以將呢啲細數據列砌返埋一齊,形成一個排好咗嘅大數據列;而頭先提到嘅對分檢索都係合併排序嘅一種-對分檢索涉及到將要排嘅數列分拆做幾橛,將嗰幾橛逐個逐個排好咗之後再併返埋一齊做個輸出[63]。
回溯法
[編輯]回溯法(backtracking)係指用遞歸噉一步一步建立一個答案,而喺發現個答案唔掂(唔符合由用家指定嘅條件)嗰陣,就放棄嗰個答案(「回溯」-返轉頭做過),郁手建立下一個答案,一路重複做,做到搵到個掂嘅答案為止。大致上可以噉樣想像[65]:
- 檢查吓搵到答案未,如果搵到(true)嘅話,終止程式;
- 建立答案嘅一步(例:如果解嘅係數獨,是但填一個可能數字),
- 如果目前狀態冇可能達到目的,噉就重新做過;
- 重複。
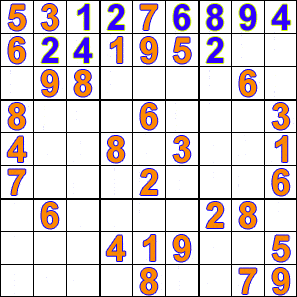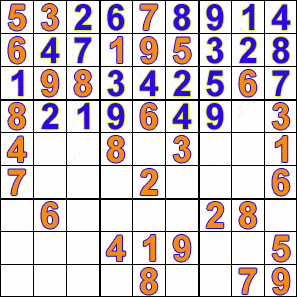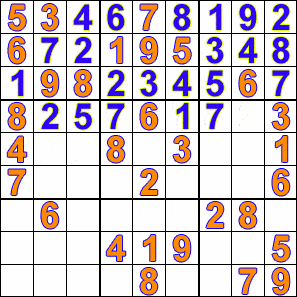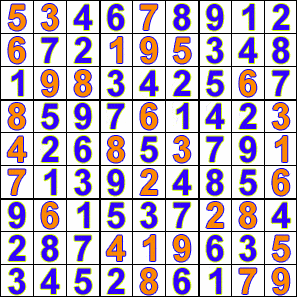
例如下圖係用回溯法解數獨嘅動畫:
按運算複雜度
[編輯]
運算複雜性理論(computational complexity theory)係運算理論嘅一個子領域,研究用演算法解決問題「有幾撈絞」-舉個例子說明,想像有個問題,先前嘅分析顯示咗,個問題係有可能用電腦解決嘅,但打後進一步嘅分析發現,解決呢個問題要用嗰串演算法複雜到就算用最先進嘅電腦行,都要用成 100 年先行得完,噉嘅話個問題喺實際應用上根本冇得有效率噉解決。對「可以解到嘅問題要嘥幾多時間空間先解到」嘅思考就係運算複雜性理論嘅重心[66][67]。
運算複雜性理論嘅分析興用大 O 符號(big O notation)嘅方法嚟表示演算法嘅運算複雜度,一個大 O 符號會將一段演算法嘅時間複雜度(time complexity;簡單講就係指段演算法嘥幾多時間)同空間複雜度(space complexity;簡單講就係指段演算法嘥幾多記憶體)表達成輸入大細嘅函數,例如一個用窮舉演算法搜尋一個數列嘅演算法喺最壞情況下要耖嗮成個數列先會搵到想要嗰個數,即係話設數列嘅長度係 ,噉呢個窮舉演算法嘅最壞情況時間複雜度用大 O 符號寫嘅話,就會係 O(n),意思即係話數值同 成正比[68]。
- 分類
而演算法可以按行嗮要幾耐嚟分類[69]:
- 恆定時間(constant time):無論輸入幾大都會嘥同樣咁多時間嘅,
O(c),當中 係一個常數。 - 線性時間(linear time):所嘥嘅時間同輸入嘅大細(以位元計)成簡單嘅正比或者反比,
O(n)。 - 對數時間(logarithmic time):所嘥嘅時間同輸入嘅大細嘅對數成正比或者反比,
O(log n)。 - 多項式時間(polynomial time):所嘥嘅時間同輸入嘅大細嘅若干次方成正比或者反比,
O(na),當中 係一個常數。 - 指數時間(exponential time):所嘥嘅時間同輸入嘅大細嘅指數函數成正比或者反比,
O(bn),當中 係一個常數。
... 等等。
某啲難題可能會有幾個(唔同複雜度嘅)演算法解決到,又有啲難題係冇已知能夠有效率解決佢哋嘅演算法嘅。因為噉,科學家好多時都要喺解難嗰陣諗用乜嘢演算法最好,而複雜性就係量度「一串演算法有幾好」嘅重要指標之一:假設其他因素不變,科學家會鍾意用最簡單最唔嘥時間嘅演算法[66][70]。
演算法設計
[編輯]
演算法設計(algorithm design)係數學同各門工程學上一個受關注嘅課題。數學家同工程師會係噉嘗試諗一啲新嘅演算法出嚟,目標係要做起嘢上嚟更加有效率,例如有好多呢啲領域嘅科學家都致力於諗一啲步驟少過現有演算法嘅新演算法出嚟-假設其他因素唔變,步驟少啲嘅演算法做起嘢上嚟會快啲[71]。演算法設計主要有以下呢啲步驟[72]:
- 定義好串演算法要解決嘅問題;
- 整返個模型嚟去描述嗰個問題;
- 諗一串演算法出嚟;
- 檢查吓串演算法有冇問題;
- 分析吓串演算法嘅運算複雜度等嘅表現指標(演算法分析);
- 實行串演算法;
- 程式測試;
- 做好啲文件上嘅紀錄。
演算法分析
[編輯]演算法分析(analysis of algorithm)係電腦科學嘅一門子領域,專門對演算法嘅各種特性作出分析,尤其係對運算複雜度嘅分析:好多時,同一個問題可以用好多個唔同嘅演算法嚟去解決;因為噉,軟件工程師同編程員等嘅人員好多時都會想知唔同嘅演算法當中邊啲好用啲,而要搵出個答案,佢哋就要知道每串演算法「所嘥嘅時間」同埋「用咗幾多行指令」等嘅資訊;某啲演算法可能(例如)用咗幾十行指令就解到第啲演算法要用成幾百行指令先解到嘅問題,前者行起上嚟會快啲,而且要儲落部電腦度嗰陣又會冇咁掗碇-自然啲人會更加鍾意用呢串演算法,例如頭先提到嘅對分檢索就俾人評定為好用過「將數列入面嘅數逐個逐個睇一次」嘅窮舉搜尋[73][74]。
原則上,最抽象化嘅演算法分析係純數學性嘅:喺演算法分析當中,研究者可以齋靠抽象嘅數學符號嚟表達啲演算法,好多時根本唔使用真嘅程式語言寫低串演算法先;雖然係噉,絕大部份嘅演算法去到最尾都係要用某啲硬件或者軟件平台嚟執行嘅,而啲演算法執行嗰陣嘅效率就會俾人攞嚟評估串演算法[75]。
演算法效率(algorithmic efficiency)係演算法分析上至關重要嘅一個概念,指緊一串演算法要用幾多資源-用咗幾多行指令、幾多款指令呀噉-嚟解決一個特定嘅問題;假設第啲因素唔變,一串演算法愈係可以用少嘅資源-用嘅指令短、唔使用啲複雜同進階嘅指令-嚟解決一個問題,串演算法就愈會俾人覺得佢有效率,而工程師同科學家一般都鍾意高效率嘅演算法[76]。高效率嘅演算法可以有用得好交關:例如係處理圖像用嘅快速傅立葉變換(Fast Fourier Transform)噉,有研究試過發現,快速傅立葉變換演算法方面嘅改進令到醫療上嘅圖像處理快咗成 1,000 倍咁多[77]。
法律問題
[編輯]一串演算法嘅專利誰屬喺法律上係一個問題。專利(patent)係指由一個國家或者地區嘅政府俾發明一樣嘢嘅人,宣佈喺一段時間內(例如廿年內)嗰樣發明專屬於嗰位發明者,而想用嗰樣發明嚟賺錢嘅人通常都要俾錢個發明者先,然後個發明者先至俾佢哋有權運用嗰樣發明嚟賺錢,軟件專利(software patent)就係泛指為咗電腦軟件-電腦程式、函式庫、用家介面同演算法等-而設嘅專利[註 7][78]。
喺廿一世紀初,「齋靠一串演算法有冇得攞去申請專利」係一個受爭議嘅課題:喺 2006 年嘅美國,一個人係唔可以齋靠玩弄抽象概念、數字或者訊號嚟攞專利嘅,所以發明一串演算法冇得攞專利;之但係演算法嘅實現成品就可能有得申請專利-例如如果有個人諗咗個新演算法出嚟,並且用某隻程式語言寫咗段源碼嚟執行呢段演算法,噉嗰個人就有可能有得為嗰段源碼申請專利,而噉做實際上就係為個演算去申請咗專利[79];不過另一方面,又有唔少人都批評容許人為軟件伸請專利嘅做法[80],例如喺 2019 年嘅印度,專利呢家嘢淨係可以為「能夠喺工業上實際使用」嘅物件申請,而電腦程式同演算法唔俾印度官方定性為噉樣嘅物件,所以冇得申請專利-即係話喺有個人喺印度發明咗串演算法,第啲人可以隨意攞嚟用[81]。
註釋
[編輯]睇埋
[編輯]文獻
[編輯]- Boolos, George; Jeffrey, Richard (1999) [1974]. Computability and Logic (4th ed.). Cambridge University Press, London. ISBN 978-0-521-20402-6.: cf. Chapter 3 Turing machines where they discuss "certain enumerable sets not effectively (mechanically) enumerable".
- Gurevich, Y. (2000). Sequential Abstract State Machines Capture Sequential Algorithms, ACM Transactions on Computational Logic, Vol. 1, no. 1, pp. 77–111.
- Knuth, Donald E. (2000). Selected Papers on Analysis of Algorithms. Stanford, California: Center for the Study of Language and Information.
- Knuth, Donald E. (2010). Selected Papers on Design of Algorithms. Stanford, California: Center for the Study of Language and Information.
- Minsky, Marvin (1967). Computation: Finite and Infinite Machines (1st ed.). Prentice-Hall, Englewood Cliffs, NJ. ISBN 978-0-13-165449-5. Minsky expands his "...idea of an algorithm – an effective procedure..." in chapter 5.1 Computability, Effective Procedures and Algorithms. Infinite machines.
- Sipser, Michael (2006). Introduction to the Theory of Computation. PWS Publishing Company. ISBN 978-0-534-94728-6.
- Stone, Harold S. (1971). Introduction to Computer Organization and Data Structures. McGraw-Hill, New York. ISBN 978-0-07-061726-1. Cf. in particular the first chapter titled: Algorithms, Turing Machines, and Programs. His succinct informal definition: "...any sequence of instructions that can be obeyed by a robot, is called an algorithm" (p. 4).
- Tausworthe, Robert C (1977). Standardized Development of Computer Software, Part 1 Methods. Englewood Cliffs NJ: Prentice–Hall, Inc. ISBN 978-0-13-842195-3.
- Turing, Alan M. (1936–37). "On Computable Numbers, With An Application to the Entscheidungsproblem". Proceedings of the London Mathematical Society. Series 2. 42: 230–265. doi:10.1112/plms/s2-42.1.230.. Corrections, ibid, vol. 43(1937) pp. 544–546.
- Turing, Alan M. (1939). "Systems of Logic Based on Ordinals". Proceedings of the London Mathematical Society. 45: 161–228.
攷
[編輯]- ↑ 1.0 1.1 "Any classical mathematical algorithm, for example, can be described in a finite number of English words." (Rogers, 1987:2).
- ↑ Well defined with respect to the agent that executes the algorithm: "There is a computing agent, usually human, which can react to the instructions and carry out the computations." (Rogers, 1987:2).
- ↑ "A procedure which has all the characteristics of an algorithm except that it possibly lacks finiteness may be called a 'computational method'." (Knuth, 1973:5).
- ↑ "An algorithm has one or more outputs, i.e. quantities which have a specified relation to the inputs." (Knuth, 1973:5).
- ↑ "an algorithm is a procedure for computing a function (with respect to some chosen notation for integers) ... this limitation (to numerical functions) results in no loss of generality", (Rogers 1987:1).
- ↑ Spall, J. C. (2003). Introduction to Stochastic Search and Optimization. Wiley.
- ↑ Cooke, Roger L. (2005). The History of Mathematics: A Brief Course. John Wiley & Sons.
- ↑ Stone, 1971.
- ↑ Boolos and Jeffrey, 1974,1999:19.
- ↑ Minsky, 1967, p. 105.
- ↑ Gurevich, 2000:1, 3.
- ↑ Stone simply requires that "it must terminate in a finite number of steps" (Stone, 1972:7–8).
- ↑ Boolos and Jeffrey, 1974,1999:19.
- ↑ Knuth, 1973:7 states: "In practice we not only want algorithms, we want good algorithms ... one criterion of goodness is the length of time taken to perform the algorithm ... other criteria are the adaptability of the algorithm to computers, its simplicity and elegance, etc."
- ↑ Stone, 1971:7-8 states that there must be, "...a procedure that a robot [i.e., computer] can follow in order to determine precisely how to obey the instruction." Stone adds finiteness of the process, and definiteness (having no ambiguity in the instructions) to this definition.
- ↑ Hodges, Andrew (2012). Alan Turing: The Enigma (The Centenary Edition). Princeton University Press.
- ↑ Petzold, C. (2008). The annotated Turing: a guided tour through Alan Turing's historic paper on computability and the Turing machine. Wiley Publishing.
- ↑ 18.0 18.1 18.2 18.3 Background: Algorithms. 互聯網檔案館嘅歸檔,歸檔日期2018年7月3號,.
- ↑ 19.0 19.1 Sipser, 2006:157.
- ↑ Lai, Hung Chi; Muroga, Saburo (September 1979). "Minimum Binary Parallel Adders with NOR (NAND) Gates". IEEE Transactions on Computers. IEEE. C-28 (9): 648–659.
- ↑ Anthony J. Pansini, Electrical Distribution Engineering, p. xiv, The Fairmont Press Inc., 2006.
- ↑ 22.0 22.1 22.2 Knuth, Donald (1998). Sorting and Searching. The Art of Computer Programming. 3 (2nd ed.). Reading, MA: Addison-Wesley Professional.
- ↑ Instantly share code, notes, and snippets. GitHubGist.
- ↑ 24.0 24.1 Flores, Ivan; Madpis, George (1 September 1971). "Average binary search length for dense ordered lists". Communications of the ACM. 14 (9): 602–603.
- ↑ Willams, Jr., Louis F. (22 April 1976). A modification to the half-interval search (binary search) method. Proceedings of the 14th ACM Southeast Conference. ACM.
- ↑ Sedgewick, Robert (1980), "Efficient Sorting by Computer: An Introduction", Computational Probability, New York: Academic Press, pp. 101–130.
- ↑ Sedgewick, R. (1978). "Implementing Quicksort programs". Comm. ACM. 21 (10): 847–857.
- ↑ Dean, B. C. (2006). "A simple expected running time analysis for randomized "divide and conquer" algorithms". Discrete Applied Mathematics. 154: 1–5.
- ↑ Quicksort with Python.
- ↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Problem 2-2, pg.40.
- ↑ Astrachan, Owen (2003). "Bubble sort: an archaeological algorithmic analysis" (PDF). ACM SIGCSE Bulletin. 35 (1): 1–5.
- ↑ "Euclid's Elements, Book VII, Proposition 2". Aleph0.clarku.edu.
- ↑ Heath, 1908:300; Hawking's Dover 2005 edition derives from Heath.
- ↑ Euclidean Algorithm. Wolfram MathWorld.
- ↑ For modern treatments using division in the algorithm, see Hardy and Wright, 1979:180, Knuth, 1973:2 (Volume 1), plus more discussion of Euclid's algorithm in Knuth 1969:293–297 (Volume 2).
- ↑ Knuth, 1973: 2-4.
- ↑ Knuth, 1973:13–18. He credits "the formulation of algorithm-proving in terms of assertions and induction" to R. W. Floyd, Peter Naur, C. A. R. Hoare, H. H. Goldstine and J. von Neumann. Tausworth 1977 borrows Knuth's Euclid example and extends Knuth's method in section 9.1 Formal Proofs (pages 288–298).
- ↑ Tausworthe, 1997:294.
- ↑ Cui, X., & Shi, H. (2011). A*-based pathfinding in modern computer games. International Journal of Computer Science and Network Security, 11(1), 125-130.
- ↑ Boyarski, E., Felner, A., Stern, R., Sharon, G., Tolpin, D., Betzalel, O., & Shimony, E. (2015, June). ICBS: improved conflict-based search algorithm for multi-agent pathfinding. In Twenty-Fourth International Joint Conference on Artificial Intelligence.
- ↑ 41.0 41.1 Millington, I. (2019). AI for Games. CRC Press. Ch. 4.
- ↑ Hagelback, Johan, and Stefan J. Johansson. "Dealing with fog of war in a real-time strategy game environment." In Computational Intelligence and Games, 2008. CIG'08. IEEE Symposium On, pp. 55-62. IEEE, 2008.
- ↑ Fletcher, Peter; Hoyle, Hughes; Patty, C. Wayne (1991). Foundations of Discrete Mathematics (International student ed.). Boston: PWS-KENT Pub. Co. p. 463. ISBN 978-0-53492-373-0. "A weighted graph is a graph in which a number w(e), called its weight, is assigned to each edge e."
- ↑ Antsfeld, L., Harabor, D. D., Kilby, P., & Walsh, T. (2012, October). Transit routing on video game maps. In Eighth Artificial Intelligence and Interactive Digital Entertainment Conference.
- ↑ Goodwin, S. D., Menon, S., & Price, R. G. (2006). Pathfinding in open terrain. In Proceedings of International Academic Conference on the Future of Game Design and Technology.
- ↑ 46.0 46.1 46.2 Integration Basics: How to integrate the equations of motion. 互聯網檔案館嘅歸檔,歸檔日期2018年10月26號,.. Gaffer on Games.
- ↑ Van der Burg, John (23 June 2000). "Building an Advanced Particle System". Gamasutra.
- ↑ 48.0 48.1 Recursion and Backtracking.
- ↑ Recursive Algorithm.
- ↑ Petković, Miodrag (2009). Famous Puzzles of Great Mathematicians. AMS Bookstore. p. 197.
- ↑ Bocchino Jr., Robert L.; Adve, Vikram S.; Adve, Sarita V.; Snir, Marc (2009). Parallel Programming Must Be Deterministic by Default. USENIX Workshop on Hot Topics in Parallelism.
- ↑ Robert W. Floyd (October 1967). "Nondeterministic Algorithms". Journal of the ACM. pp. 636–644.
- ↑ What Is RNG in Video Games, and Why Do People Criticize It? 互聯網檔案館嘅歸檔,歸檔日期2019年12月9號,.. How-To Geek.
- ↑ Gary McGraw and John Viega. Make your software behave: Playing the numbers: How to cheat in online gambling.
- ↑ Learning process of a neural network 互聯網檔案館嘅歸檔,歸檔日期2021年2月11號,.. Towards Data Science.
- ↑ Bernard., Shmoys, David (2011). The design of approximation algorithms. Cambridge University Press.
- ↑ For instance, the volume of a convex polytope (described using a membership oracle) can be approximated to high accuracy by a randomized polynomial time algorithm, but not by a deterministic one: see Dyer, Martin; Frieze, Alan; Kannan, Ravi (January 1991), "A Random Polynomial-time Algorithm for Approximating the Volume of Convex Bodies", J. ACM, New York, NY, USA: ACM, 38 (1): 1–17.
- ↑ Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, pp. 111–114.
- ↑ Carroll, Sue; Daughtrey, Taz (July 4, 2007). Fundamental Concepts for the Software Quality Engineer. American Society for Quality. pp. 282.
- ↑ Computer Chess - A Memorial to BRUTE FORCE.
- ↑ Allis, L. V. Searching for Solutions in Games and Artificial Intelligence. PhD thesis, Univ. Limburg, Maastricht, The Netherlands (1994).
- ↑ van den Herik, H., Uiterwijk, J. W. & van Rijswijck, J. Games solved: now and in the future. Artif. Intell. 134, 277–311 (2002).
- ↑ 63.0 63.1 Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest, Introduction to Algorithms (MIT Press, 2000).
- ↑ Blahut, Richard. Fast Algorithms for Signal Processing. Cambridge University Press. pp. 139–143.
- ↑ Backtracking Algorithms. GeeksForGeeks.
- ↑ 66.0 66.1 Arora, Sanjeev; Barak, Boaz (2009), Computational Complexity: A Modern Approach, Cambridge University Press.
- ↑ Braatz, R. P., Young, P. M., Doyle, J. C., & Morari, M. (1994). Computational complexity of/spl mu/calculation. IEEE Transactions on Automatic Control, 39(5), 1000-1002.
- ↑ Black, Paul E. (11 March 2005). Black, Paul E. (ed.). "big-O notation". Dictionary of Algorithms and Data Structures. U.S. National Institute of Standards and Technology.
- ↑ Sipser, Michael (2006). Introduction to the Theory of Computation. Course Technology Inc.
- ↑ Kolen, J. F., & Hutcheson, T. (2002). Reducing the time complexity of the fuzzy c-means algorithm. IEEE Transactions on Fuzzy Systems, 10(2), 263-267.
- ↑ Mohr, Austin. "Quantum Computing in Complexity Theory and Theory of Computation". p. 2. Retrieved 7 June 2014.
- ↑ Goodrich, Michael T.; Tamassia, Roberto (2002), Algorithm Design: Foundations, Analysis, and Internet Examples, John Wiley & Sons, Inc.
- ↑ Goldreich, Oded (2010). Computational Complexity: A Conceptual Perspective. Cambridge University Press.
- ↑ Sedgewick, Robert; Flajolet, Philippe (2013). An Introduction to the Analysis of Algorithms (2nd ed.). Addison-Wesley.
- ↑ Greene, Daniel A.; Knuth, Donald E. (1982). Mathematics for the Analysis of Algorithms (Second ed.). Birkhäuser.
- ↑ Kriegel, Hans-Peter; Schubert, Erich; Zimek, Arthur (2016). "The (black) art of runtime evaluation: Are we comparing algorithms or implementations?". Knowledge and Information Systems. 52 (2): 341–378.
- ↑ Gillian Conahan (January 2013). "Better Math Makes Faster Data Networks". discovermagazine.com.
- ↑ Bessen, James; Meurer, Michael (2008). Patent Failure. Princeton University Press.
- ↑ Patents for computer-related inventions. IP Australia.
- ↑ Nichols, Kenneth (1998). Inventing Software: The Rise of "computer-related" Patents. Greenwood Publishing Group. p. 15.
- ↑ Can you Patent a Software?.
拎
[編輯]- The Stony Brook Algorithm Repository – State University of New York at Stony Brook.
- Collected Algorithms of the ACM – Association for Computing Machinery.
- The Stanford GraphBase – Stanford University.
- Dictionary of Algorithms and Data Structures – National Institute of Standards and Technology

































