 一條基本嘅
一條基本嘅 。
。
對數係一種函數,佢係指數函數嘅反函數。對數係嚟自指數,指數函數嘅基本樣係 ,
, 係一個正實數。咁呢個圖就會穿過
係一個正實數。咁呢個圖就會穿過 ,同埋x軸就係呢個圖嘅趨近線(asymptote)。因為指數函數係單對單函數,又係全射函數,所以佢就會有逆函數或者叫相反。而指數函數嘅相反就係對數,求出黎嘅方法可以參考下面。
,同埋x軸就係呢個圖嘅趨近線(asymptote)。因為指數函數係單對單函數,又係全射函數,所以佢就會有逆函數或者叫相反。而指數函數嘅相反就係對數,求出黎嘅方法可以參考下面。
對數有好多唔同嘅作用,其中最常見嘅就有搵出次方,同埋做數學建模去解決現實世界嘅問題。
如果利用簡介所提及嘅方法嚟搵對數,就要根據以下步驟:
- 將
 :
:
- 將
 同
同 交換:
交換:
- 求
 :
:
設  ,
, 同埋
同埋  ,對數函數(logarithmic function)
,對數函數(logarithmic function) 符合:
符合:
「 」。
」。
呢個函數嘅基數(或叫基底,英文:base)就係  。「
。「 」 中文一般會讀成「log
」 中文一般會讀成「log  底
底  」;英文一般會讀成「log base
」;英文一般會讀成「log base  of
of  」。有啲計數機將
」。有啲計數機將  寫做
寫做  ,有啲寫做
,有啲寫做  。
。
根據以上呢個定義, ,
, 呢兩個表達係完全一樣。
呢兩個表達係完全一樣。
一般會將 叫做指數表示(exponential form);
叫做指數表示(exponential form);
另一個樣, 叫做對數表示(logarithmic form)。
叫做對數表示(logarithmic form)。




求一個對數嘅絕對值需要用到代數技巧。
例如求:
- 將求嘅數等於
 :
:
- 利用等價定義轉返佢做指數表示:

- 解方程:

- 還原答案:

例子:

有自然指數就自然有自然對數,佢哋基本大同小異,只不過自然對數個基數係歐拉數 。而一般情況普通對數個基數就係
。而一般情況普通對數個基數就係 ,叫做常用對數。
,叫做常用對數。
通常用基數係 嘅情況,本嚟係要寫成
嘅情況,本嚟係要寫成 ,但係因為成日用嘅關係,多數人都會寫成
,但係因為成日用嘅關係,多數人都會寫成 咁,而唔寫基數就默認係
咁,而唔寫基數就默認係 。為咗避免誤會(例如高等數學入面嘅
。為咗避免誤會(例如高等數學入面嘅  好多時係以
好多時係以  做底),有時又會寫做
做底),有時又會寫做 。
。
如果用歐拉數 做基數,本嚟係要寫成
做基數,本嚟係要寫成 ,因為喺數學上好多時會用到,所以數學家就發明咗個符號寫做
,因為喺數學上好多時會用到,所以數學家就發明咗個符號寫做 ,所有基數係
,所有基數係 嘅對數,就會寫成
嘅對數,就會寫成 。呢個叫做自然對數。
。呢個叫做自然對數。
喺某啲領域,成日會用到  做基數,本嚟係要寫成
做基數,本嚟係要寫成  ,簡化寫成
,簡化寫成  。
。
因為對數係指數嘅逆函數,所以可以利用 反射
反射 得出
得出 。
。
 如果
如果 。
。
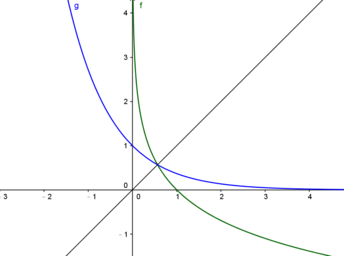
如果 就會得出上面呢張圖嘅樣,藍色線就係
就會得出上面呢張圖嘅樣,藍色線就係 ,將佢根據
,將佢根據 ,黑線,做一個反射就得出綠色線
,黑線,做一個反射就得出綠色線 。
。
 如果
如果 。
。
如果 就會得出上面呢張圖嘅樣,藍色線就係
就會得出上面呢張圖嘅樣,藍色線就係 ,將佢根據
,將佢根據 ,黑線,做一個反射就得出綠色線
,黑線,做一個反射就得出綠色線 。
。
以下呢個表可以比較指數同對數函數嘅相似同唔同之處:
| 指數函數

|
對數函數

|
 軸相交點係 軸相交點係
|
 軸相交點係 軸相交點係
|
函數域(Domain)係
|
函數域(Domain)係
|
Range係
|
Range係
|
趨近線係 軸 軸
|
趨近線係 軸 軸
|
對數可以做好多現實中嘅應用,以下舉出幾個出名嘅應用:
分貝(decibel)係量度噪音程度嘅單位。佢係利用對數呢個概念。
分貝值喺數學上定義為:
式入面嘅  就係分貝值,單位係 dB。
就係分貝值,單位係 dB。 就每平方米嘅聲音強度,單位係瓦特(watt)。
就每平方米嘅聲音強度,單位係瓦特(watt)。 就係人最低可以聽到嘅噪音強度。平均嚟講,一般人最低可以聽到最低噪音係
就係人最低可以聽到嘅噪音強度。平均嚟講,一般人最低可以聽到最低噪音係  。
。
黎克特制(Richter scale)係用嚟量度地震強度。
計算呢個強度嘅公式係: ,
,
當中  係強度,
係強度, 係地震震波強度,
係地震震波強度, 係地震所釋出嘅能量。
係地震所釋出嘅能量。
喺化學入邊,pH值亦即係酸鹼度係用對數嚟定義嘅。
ph值公式:![{\displaystyle {\textrm {pH}}=-\log _{10}[{\textrm {H}}^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57df1eef84ee0344198a3cf2bdfdcb5d60edcae6) ,
,
當中 ![{\displaystyle [{\textrm {H}}^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e034bd4077ba0143e208e504504c8bde1160f26b) 係氫離子嘅濃度。[1]
係氫離子嘅濃度。[1]






























































![{\displaystyle {\textrm {pH}}=-\log _{10}[{\textrm {H}}^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57df1eef84ee0344198a3cf2bdfdcb5d60edcae6)
![{\displaystyle [{\textrm {H}}^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e034bd4077ba0143e208e504504c8bde1160f26b)