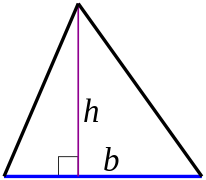
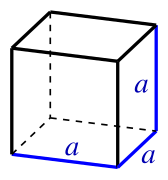
幾何學

幾何學會思考形狀、線同角度等嘅特性。

幾何學（粵拼：gei2 ho4 hok6；古希臘文：γεωμετρία / geometria）係數學其中一個分科，專門思考有關形狀、物體嘅相對位置以及空間嘅特性等嘅課題。幾何學理論以點、直線、平面、角以及維度等嘅概念為基礎，會用數學證明嘅方法，證明描述呢啲概念嘅定理，靠噉嚟增進人類對呢啲概念同埋相應嘅現實世界物體嘅理解。

幾何學歷史悠久：公元前嘅古希臘等多個遠古文明都有獨立噉建立幾何學方法諗長度、面積同容量等嘅概念，用嚟做設計建築等嘅多種用途；形式化嘅幾何學源於古希臘，喺公元前 3 世紀，古希臘數學家歐幾里得喺佢本名著《幾何原本》當中用公理化嘅方法證明咗多條幾何學上嘅定理，為後世嘅幾何學研究奠定咗重要嘅根基。而中世紀（5 至 15 世紀）同埋打後嘅數學家亦一直有將幾何學再發展上去。去到現時（廿一世紀初），幾何學都係活躍嘅研究領域。

喺廿一世紀初，幾何學知識相當有影響力，喺好多科學同工程學領域上都相當有用，例如：古典力學喺分析物體嘅移動嗰陣，成日都會用到距離同速率等建基於幾何學嘅概念；電腦圖像泛指用電腦整嘅圖像，而一部電腦整 3D 模型嗰時要做運算，中途用到「個模型呢條邊有幾長」同「個模型呢隻角有幾大」噉嘅資訊；建築學研究建築物嘅設計，會對建築物作出幾何分析－建築物唔同部位嘅角度同長度會影響棟建築物穩唔穩陣呀噉。

空間基礎

平面上面一拃點；每粒點都可以想像成「塊平面」呢個集入面嘅元素。

内文：空間同空間 (數學)

睇埋：維度同笛卡兒坐標系統

幾何學係研究空間嘅數學子領域。「『空間』呢個概念要點定義」可以幾撈絞，不過喺最基本（歐幾里得幾何）上，空間可以用點、直線同埋平面等嘅概念想像。

0D：點

内文：點 (幾何)

睇埋：0D 空間

點係幾何學上嘅原始諗法：

• 簡化噉講，點可以定義做「喺空間裡面有確切位置、唔佔用空間嘅嘢」，冇長度同闊度；
• 技術化啲講，現代數學有咗集合論，而喺呢套理論框架下，點通常俾人定義做「一個集（空間）入面嘅其中一件元素」，例如想講一塊平面上面嘅一點，首先就會定義塊平面係

  $\mathbb {R} ^{2}=\{(a,b):a,b\in \mathbb {R} \}$，

塊平面上嘅一點 $p$ 就係 $\mathbb {R} ^{2}$ 入面嘅元素；用日常用語講嘅話，即係 $p$ 可以寫做 $(a,b)$，當中 $a$ 同 $b$ 都係實數（$\mathbb {R}$）。值得一提嘅係，點原則上係抽象化嘅概念，淨係存在喺人嘅想像之中：理論上嘅點係冇長度同闊度嘅，而當一個人攞支筆畫一粒肉眼睇得到嘅點嗰陣（好似下圖噉），嗰點查實經已有返咁上下長度同闊度，所以人先可以用肉眼睇得到，嚴格嚟講唔可以算係一點，頂嗮攏只可以算係攞嚟表示一點嘅符號。

點係幾何學最根基嘅諗頭－有咗點嘅概念，就有得定義同闡述第啲重要嘅幾何學概念同諗法，例如「是但兩點之間，都可以畫條獨一無二嘅線」呢條公理噉。

1D：直線

内文：直線

睇埋：1D 空間同間尺

直線係幾何學想像中一種「冇闊度、有長度嘅嘢」，當中「直」係指「上面啲點均勻噉分佈嘅線」：

• 攞住點嘅概念，想像攞是但兩點 $A$ 同 $B$，喺 $A$ 同 $B$ 之間有無限咁多粒點，嗰啲點之間每對點之間嘅距離都係恆定嘅（$=0$）；
• 用集合論嘅角度嚟睇嘅話，一條線可以想像成由一大拃點組成嘅集－精確啲講，喺現代幾何學入面，直線通常俾人定義做「喺個線性空間入面，有某種線性關係嘅點集」；是但攞一粒點 $p$ 同一條線 $\ell$ 嚟睇，「$p$ 喺 $\ell$ 上面」或者「$p$ 唔喺 $\ell$ 上面」都會係有意義嘅句子－句嘢一係真一係假。
• 平面入面嘅直線有個性質，就係是但搵兩點，嗰兩點都可以用一條直線連接（睇返歐幾里得幾何嘅第一公理），而且喺所有「能夠連接兩點嘅線」之中直線係長度最短嘅；

好似下圖噉就係一條「線」－下圖條線實質上有闊度（如果唔係就唔會用肉眼睇得到），所以只係用嚟表示一條線嘅符號。

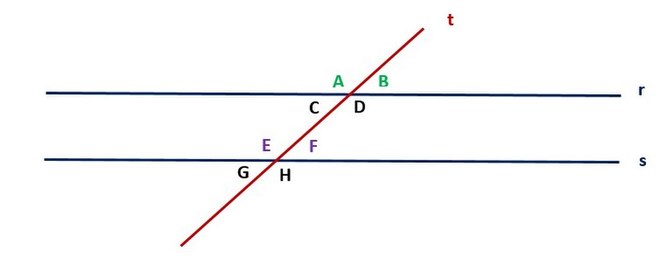
喺歐幾里得幾何入面，兩條直線之間可以有交點（一粒同時屬嗰兩條線嘅點），又可以有平行嘅關係－如果話兩條線係平行嘅，意思係話無論將嗰兩線延長幾多都好，兩條線都唔會有交點。好似下圖噉，下圖有三條線 $t$、$r$ 同 $s$，當中 $t$ 同 $r$ 喺 ABCD 嗰點（頂點）相交，而 $t$ 同 $s$ 喺 EFGH 嗰點（都係頂點）相交，$r$ 同 $s$ 平行：

直線仲可以掕埋「曲線」嘅概念：曲線係一種幾何物體；同直線一樣，曲線可以想像成由兩點之間嘅點組成嘅集，不過曲線「可能係唔直嘅」嘅（好似下圖噉）；技術化噉講，曲線可以想像成直線嘅廣義化－「線」可以包嗮所有「由兩點之間嘅點組成嘅集」，而直線就計係線嘅一種，特指「上面啲點均勻噉分佈嘅線」。

2D：平面

内文：平面

睇埋：曲面同2D 空間

喺歐幾里得幾何裏面，一塊平面係一塊 2D 而且冇曲率嘅幾何物體，有長度同闊度但冇高度，（最少理論上）可以向住任何方向無限噉延伸。如果用最常用嗰隻坐標系統嚟諗嘅話，平面同直線嘅分別可以想像成「要用幾多個數先可以描述一點嘅位置」（睇埋維度同坐標等嘅概念）－

• 如果要描述一點喺條線上面邊個位，淨係要用一個數，例如 $(x)$，所以係一維（1D）；
• 而如果要描述一點喺塊平面上面邊個位，就要用兩個數至得，例如 $(x,y)$，所以係二維（2D）；

下圖係互相成平行嘅三塊平面（想像三塊平面都冇高度－即係無限咁薄）：

歐幾里得研究嘅幾何好大部份都係喺平面入面發生嘅幾何（即係所謂嘅平面幾何），包括咗平面上面嘅三角形、圓形、平行線同角度呀噉。而根據呢套研究，平面有好多特別嘅性質：

• 是但攞兩塊唔同嘅平面，佢哋一係彼此成平行、一係就會係某條線嗰度相交；
• 是但攞一塊平面同一條線，條線一係同塊平面成平行、一係會喺某點同塊平面相交、再唔係就可能喺塊平面上面；
• 如果有兩條唔同嘅線，兩條都係同一塊平面成垂直（簡化講就係成 90° 角），噉兩條線實係平行嘅；
• 如果有兩塊平面都同某條線成垂直，噉兩塊平面實係成平行嘅。

兩塊相交兼成垂直嘅平面 兩塊相交兼成垂直嘅平面  線 同平面 成垂直。 線 $\ell$ 同平面 $A$ 成垂直。  線 同啲平面成垂直，啲平面彼此平行。 線 ${\text{S}}$ 同啲平面成垂直，啲平面彼此平行。

圓形係一種 2D 嘅形狀；用坐標諗嘅話，圓形條邊上面嘅每一點 $(x,y)$ 都會滿足以下條式－
$(x-a)^{2}+(y-b)^{2}=r^{2}$
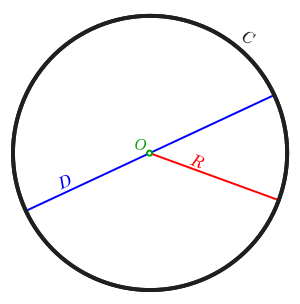
當中 $(a,b)$ 係個圓心嘅坐標值，而 $r$ 係個圓形嘅半徑有幾長。

一去到 2D，就可以諗埋角嘅概念：是但攞一點（例如下圖嘅 $A$），由嗰點向住兩個方向（例如下圖嘅 $C_{1}$ 同 $C_{3}$）各射一條直線出去嘅話，兩條射線之間就會形成一隻角（下圖 $\alpha _{2}$），而角度就係一隻角可以有嘅特性，反映隻角「有幾大」；喺實際嘅幾何分析上，一隻角通常會用 $\angle$ 嘅符號嚟表示，下圖嘅 $\alpha _{2}$ 會寫做 $\angle C_{1}AC_{3}$ 噉嘅樣，而且會用噉嘅符號表示啲角嘅大細－$\angle ABC=90$ 表示「$\angle ABC$ 呢隻角係 90° 咁大」... 如此類推。

3D 或以上

内文：立體

睇埋：3D 空間、歐幾里得空間同4D 空間

有咗點、直線、曲線、平面同角呢啲基本概念，研究者就可以對現實世界嘅空間做出基本嘅分析：3D 空間指笪空間入面嘅每個可能點都要有三個數 $(x,y,z)$，先可以講明佢喺邊個位－人類日常生活當中會接觸到嘅世界，就可以想像成一笪 3D 空間，有三條完全直嘅軸；响呢笪 3D 空間裏面，

• 每件物體都有長度、闊度同高度表示佢「掗咗幾多空間」，
• 每件物體都可以沿三條軸郁動－可以有前後左右上下一共六個方向；

一笪 3D 空間會有好多點，可以有直線、曲線同平面，而線之間或者平面之間（或者線同平面之間）可以有角度。

球體；當中 係個球體嘅半徑。 球體；當中 $r$ 係個球體嘅半徑。  立方體；定義上，立方體每條邊都一樣咁長，而且是但搵其中兩條邊睇，嗰兩條邊都成直角。 立方體；定義上，立方體每條邊都一樣咁長，而且是但搵其中兩條邊睇，嗰兩條邊都成直角。  3D 空間嘅旋轉動畫；喺一笪 3D 空間入面，一點嘅位置可以表示做 噉嘅樣，當中每個數表示嗰點沿其中一條軸嘅位。 3D 空間嘅旋轉動畫；喺一笪 3D 空間入面，一點嘅位置可以表示做 $(x,y,z)$ 噉嘅樣，當中每個數表示嗰點沿其中一條軸嘅位。

對 3D 或以上維度嘅空間嘅分析好有用。幾何學家會用數學證明嘅方法，探究點、線同埋空間有咩特性，而第啲領域嘅工作者就可以攞住呢啲知識去做嘢：喺廿一世紀初嘅多數工程學應用上，分析空間嘅特性可以齋靠「將空間想像成笪 3D 空間，而且每個位置都可以用實數坐標表示」就搞得掂－呢種分析可以攞嚟分析交通工具（汽車等嘅嘢郁動，就係改變喺空間入面嘅位置）同建築物（一棟建築物會有長度、闊度同高度）等工程學上會想分析嘅嘢；古典物理學上嘅分析可以齋靠 3D 就搞得掂，而進階嘅物理學－例如廣義相對論－仲會用到多過三個維度嚟描述時空。

理論基礎

保角映射；雖然有啲直線變咗曲線，但如果兩條線原本係成直角嘅話，出嚟嘅兩條曲線都會成直角。

内文：幾何學理論基礎

睇埋：集合論

幾何學理論基礎係指嘗試用公理化嘅方式推導出一套有系統嘅幾何學嘅數學研究。喺建立幾何學理論嗰陣，數學家希望做到齋靠以下幾樣嘢砌出一個內部一致（即係唔能夠由個理論嗰度推導出邏輯矛盾）嘅理論：

• 原始諗法：即係一啲最基本、唔使定義嘅概念，例如點同直線等嘅概念喺歐幾里得嗰套幾何理論當中係原始諗法，而唔係原始諗法嘅概念就要用原始諗法嚟定義，例如「兩條線嘅相交點」會用點以及直線呢兩個概念嚟定義；
• 公理：即係一啲描述原始諗法、被認為係不證自明嘅陳述式，而且唔能夠由第啲公理嗰度推理出嚟，例如「是但搵任何兩點，都有可能畫條通過呢兩點嘅直線」就係歐幾里得嗰套幾何理論嘅其中一條公理，即係歐幾里得認為呢句嘢好明顯，唔使證明都可以當係真確；
• 邏輯上嘅定律；

數學家一般都希望一套幾何學理論所用嘅原始諗法同公理數量有咁少得咁少（可以睇埋奧坎剃刀）；喺有咗啲原始諗法同公理之後，數學家就會做數學證明，嘗試由公理同邏輯上嘅定律嗰度證明新嘅定理，最後呢啲公理同定理就形成一套幾何理論。喺廿一世紀，有唔少數學家仲喺度思考（例如）有冇方法可以用某啲被認公理嘅陳述式嗰度，推理出第啲被認為係公理嘅陳述式，諗住噉做可能幫到手建立一套用嘅公理數量更加少嘅幾何理論。

歐氏公理

睇埋：歐幾里得幾何

歐幾里得幾何係由著名古希臘數學家歐幾里得諗出嚟嘅一套幾何學，亦係公元頭嗰兩個千年內嘅標準幾何學。响佢本名著《幾何原本》裏面，歐幾里得提出咗五條公理，以「假設咗呢五條公理係真確」做前提嚟諗幾何學：

1. 是但搵兩點 $a$ 同 $b$ 嚟睇，嗰兩點之間都可以有條獨一無二嘅直線將兩點連接埋一齊。
2. 一條直線（最少理論上）可以無限噉延長。
3. 有咗「圓心」同「直徑」呢兩樣資訊，就可以建構圓形。
4. 所有嘅直角冚唪唥都係一個板嘅。
5. 平行公設：是但搵條線 $L$ 同點 $p$，當中 $p$ 唔喺 $L$ 上面，都實會有一條獨一無二嘅直線會係通過 $p$ 得嚟又唔會同 $L$ 相交嘅－即係話呢條線同 $L$ 平行。而如果兩條線之間唔係平行，噉兩條線無限延長最後實會令到兩條線相交（好似下圖噉）。

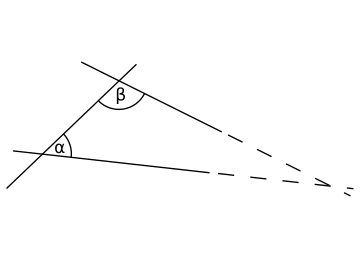
然後歐幾里得就攞住呢五條公理、用數學證明嘅方法證明嗮當時已知嘅幾何學定理。喺歐幾里得之後，仲有數學家試過對呢拃公理嘅具體定義作出修改－即係將條公理嘅定義改做比較清楚易明嘅形式，但改前改後拃公理都係可以攞嚟證明已知嘅幾何定理嘅。

重要概念

大細

内文：長度、面積同體積

長度（$l$）、面積（$A$）同體積（$V$）都係講緊一嚿幾何物體嘅「大細」（掗咗幾多空間），不過係講緊唔同維度嘅大細－1D 嘅物體，例如直線、射線同曲線呢啲物體嘅大細，就叫長度；呢個數值可以大致想像成「反映緊條線由幾多粒點組成（亦可以睇返集合）」，條線有嘅點數量愈多，長度數值就愈高。如果嚿物體係 2D 或者以上嘅話：

• 面積係三角形、圓形同曲面等 2D 物體可以有嘅特性，每種主要 2D 物體嘅面積都有條特定嘅式計－
  • 長方形：$A=ab$，當中 $a$ 同 $b$ 係個長方形嘅長度同闊度。
  • 圓形：$A=\pi r^{2}$，當中 $\pi$ 係圓周率而 $r$ 係個圓形嘅半徑。
  • 三角形：$A=(1/2)(bh)$，當中 $b$ 係底嗰條邊嘅長度而 $h$ 係高度... 等等。

長方形 長方形  圓形 圓形  三角形 三角形

• 一嚿 3D 物體塊表面可以有面積，而嚿物體本身可以有體積，反映佢嘅大細；同 2D 一樣，每種主要 3D 物體嘅體積都有條特定嘅式計－
  • 正方體：$V=a^{3}$，當中 $a$ 係個正方體嘅邊有幾長（正方體定義上就係條條邊一樣咁長嘅）。
  • 球體：$V=(4/3)\pi r^{3}$，呢度 $\pi$ 係圓周率而 $r$ 係個球體嘅半徑。
  • 圓柱體：$V=\pi r^{2}h$，當中 $r$ 係個（呈圓形嘅）底嘅半徑而 $h$ 係個柱體嘅高度... 等等。

正方體 正方體  球體 球體  圓柱體 圓柱體

好似上述噉嘅公式可以攞嚟計啲簡單嘅形狀嘅面積同體積。至於複雜啲嘅形狀嘅面積同體積要點計，可以睇吓（黎曼）積分同勒貝格積分等嘅課題。順帶一提，喺高等嘅數學入邊（大學或以上），好多時啲人或者啲書會將長度、面積同體積等嘅概念一律統稱做體積，唔理佢嘅維度係乜都照樣噉叫。

對稱

内文：對稱

對稱係數學物體可以有嘅一種特性。嚴格噉講，如果話一嚿數學物體係對稱嘅，意思即係話嚿物體經歷咗反射同轉動等嘅轉換，嚿物體都唔會變。舉例說明，鏡射係最基本嗰種對稱，指一嚿物體就算經歷咗反射都唔會變樣：簡化噉講，反射可以想像成

• 攞一個形狀（例如下圖嘅三角形 $abc$）同一條線（同一幅圖條 Y 軸），條線就叫做反射軸；
• 喺條線嘅另一邊建構個新嘅形狀（三角形 $a'b'c'$）；
• 原本個形狀嘅每一點 $p_{0}$，都喺新形狀度有個對應點 $p_{1}$，而且
• 是但攞對噉嘅兩點嚟睇，「$p_{0}$ 同反射軸之間嘅距離」等同「$p_{1}$ 同反射軸之間嘅距離」。

想像有件物體經歷咗反射，佢反射前個形狀反射後嘅形狀完全一樣（除咗位置之外），噉件物體就算係具有鏡射嘅對稱特性。進階啲嘅對稱分析，仲有講到轉動對稱（指件物體就算經歷若干角度嘅轉動都唔會變樣，例子可以睇吓三曲腿圖嘅 3-重轉動對稱）等嘅進階對稱類型。

對稱呢個概念，視覺藝術成日都會用到－好多人都認為對稱嘅物件好有美感，例如建築設計就好興將啲建築物設計到左右對稱噉嘅樣。

三角形 沿 Y 軸反射，得出 呢個新嘅三角形。 三角形 $abc$ 沿 Y 軸反射，得出 $a'b'c'$ 呢個新嘅三角形。  呢個梯形有左右鏡射對稱特性。 呢個梯形有左右鏡射對稱特性。  隻蝴蝶（金鳳蝶）大致左右鏡射對稱。 隻蝴蝶（金鳳蝶）大致左右鏡射對稱。

上圖件物體轉動咗 咁多角度。 上圖件物體轉動咗 $\alpha$ 咁多角度。  三曲腿圖有 3-重轉動對稱－如果將幅圖慢慢順時針轉，由 0° 去 360° 之間會有三次「幅圖同開始嗰陣一樣樣」。 三曲腿圖有 3-重轉動對稱－如果將幅圖慢慢順時針轉，由 0° 去 360° 之間會有三次「幅圖同開始嗰陣一樣樣」。  印度阿格拉嘅泰姬陵座主陵墓好出名，畀好多人覺得好靚，亦都係世上最左右對稱嘅建築物之一。 印度阿格拉嘅泰姬陵座主陵墓好出名，畀好多人覺得好靚，亦都係世上最左右對稱嘅建築物之一。

形狀相似

内文：全等同相似

全等同相似係兩個緊密相關嘅概念，都係用嚟講兩件幾何物體「有幾類似」，定義上：

• 兩件物體「全等」，若且唯若佢哋喺形狀同大細都相同，或者係鏡像而且大細相同－想像有兩個三角形，如果佢哋全等，攞其中一個三角形，佢入面每隻角都會同另外嗰個三角形入面嘅其中一隻角相等，而且兩者啲邊完全一樣；如果話 $A$ 同 $B$ 全等，噉就表示 $A$ 可以齋靠移位、轉動或者反射就變成 $B$，反之亦然；
• 兩件物體「相似」，若且唯若佢哋喺形狀上相等（或者係鏡像），但佢哋可以喺大細上唔同－又想像有兩個三角形，如果佢哋相似，攞其中一個三角形，佢入面每隻角都會同另外嗰個三角形入面嘅其中一隻角相等，不過兩者啲邊唔一樣，大細都唔同；如果話 $A$ 同 $B$ 相似，噉就表示要將 $A$ 變成 $B$，除咗移位、轉動或者反射之外，仲要做埋縮放先得；

變換幾何學推廣咗全等同相似嘅概念，研究喺唔同嘅變換之下邊啲幾何性質係唔變嘅。

移位 移位  轉動 轉動  反射 反射  縮放 縮放

例如下圖嗰四個三角形噉：

• （由左邊數起）第一個同第二個三角形彼此全等；
• 佢哋同第三個三角形相似；
• 而第四個三角形既唔同佢哋全等又唔同佢哋相似。

順帶一提，失蹤嘅正方形呢條出名數學謎題嘅解法，就用咗相似三角形嘅概念。

碎形

内文：碎形

睇埋：遞歸 (電腦科學)

喺數學上，碎形係一類嘅幾何形狀，指隻形狀無論規模縮到幾細都好，都會具有仔細結構，好多碎形仲會具有自相似（指一件物體同佢其中一部份相似）嘅特性。

例如曲氏雪花噉就係一隻好出名嘅碎形，有自相似特性，一塊曲氏雪花嘅整法（簡化噉講）如下：

1. 首先，攞住個等邊三角形（三條邊一樣咁長、三隻內角都係 60° 嘅三角形）；
2. 同每條邊，做以下步驟
   • 將條邊分做三橛，三橛一樣咁長；
   • 用中間嗰橛做底邊，畫個新嘅等邊三角形，呢個三角形要指向外；
   • 將上一步入面攞嚟做底邊嗰條線剷走；
3. 步驟 2 產生嗰啲新三角形，每個都攞嚟做步驟 1 同 2，同時忽略嗰啲剷走咗嘅底邊。

可以睇埋電腦科學上講嘅遞歸概念。想像將上面嘅過程無限噉重複，就會出好似下面幅 gif 噉嘅情況。好似曲氏雪花噉嘅碎形有好多畀人覺得係得意嘅特徵－例如攞住塊真正嘅曲氏雪花，再慢慢噉望近啲，會發覺無論望到幾近，塊雪花都仲會有更加細嘅三角形（仔細結構），而且啲細結構同大結構相似（自相似）。

碎形喺唔少自然現象度都可以睇到－可以睇吓雪花同自然形態規律。而且碎形畀好多人覺得好得意，所以仲有畀人應用落去建築設計同演算法藝術度。

幾何作圖

内文：尺規作圖

睇埋：間尺、圓規同電腦圖像

要研究幾何學，其中一樣重要工作係將啲幾何物體畫出嚟（幾何作圖）。尺規作圖係指齋靠間尺（可以攞嚟畫直線嘅架生）同埋圓規（可以攞嚟畫圓形嘅架生）嚟建構各種嘅幾何物體，途中唔准靠量角器。

尺規作圖係幾何學史上非常重要嘅一環：要研究幾何學，就要做到將啲幾何物體畫出嚟；廿世紀打前嘅幾何學研究者並冇電腦呢樣現代架生，所以佢哋要（簡化講）整啲原始嘅間尺同圓規，仲要證明到呢啲間尺同圓規真係畫到直線同圓形出嚟；而有咗畫直線同圓形嘅方法，佢哋就要靠呢兩樣嘢畫出更多唔同嘅幾何物體（尺規作圖），噉先至可以研究幾何學。

例如係下面中間嗰幅圖，係用尺規作圖畫正六角形（正六角形 = 六隻角完全相同大細嘅六角形）：

1. 首先畫一條夠長嘅直線；
2. 以直線上嘅一點 $O$ 做圓心，畫個圓形；
3. 攞條直線同圓形 $O$ 相交嗰兩點做兩個新圓心，畫兩個新嘅圓形；
4. 用下圖嘅方法，喺直線同圓形 $O$ 相交嗰兩點、新圓形同圓形 $O$ 相交嘅點呢啲點之間畫直線，得出一個正六角形；

嚴格嘅幾何學上，仲會用方法證明上述嘅方法真係會畫到個正六角形（證明六角形嗰六隻角真係相等）。

遠古數學家冇量角器，要點齋靠間尺同圓規畫個正六角形（隻隻角一樣咁大）呢？ 遠古數學家冇量角器，要點齋靠間尺同圓規畫個正六角形（隻隻角一樣咁大）呢？  呢段動畫描述古希臘數學家歐幾里得點樣齋靠間尺同圓規畫出正六角形。 呢段動畫描述古希臘數學家歐幾里得點樣齋靠間尺同圓規畫出正六角形。  齋靠間尺同圓規條線平分隻角 齋靠間尺同圓規條線平分隻角

自從廿世紀起，電腦技術日益進步，啲人可以輕易噉靠電腦畫圖形。有關「點樣用電腦畫幾何物體」呢條問題，可以睇吓電腦圖像同 Processing 等嘅課題。

子領域

幾何學歷史悠久，閒閒哋有得追溯到去古希臘。幾何學理論經歷過幾千年嘅發展，自然出咗唔少分枝領域：

非歐幾何

内文：非歐幾里得幾何

睇埋：球面幾何同雙曲幾何

非歐幾里得幾何，簡稱非歐幾何，係 19 世紀中興起嘅一啲幾何理論框架：喺 19 世紀中打前，歐幾里得幾何一路係幾何學嘅主流；呢套理論框架建基於歐幾里得提出嗰五條公理（睇返上面），仲跟手定義咗角度、圓形同三角形等嘅概念；非歐幾里得幾何就係一類嘅幾何理論框架，可以分好多款，共同特徵係「會否定歐氏幾何嘅某啲基本諗法」。

舉例說明，球面幾何就否定咗歐氏幾何嘅多條基本假設。球面幾何研究嘅係球體嘅 2D 表面啲幾何特性；喺球體嘅 2D 表面上，歐氏幾何所講嘅

「

是但搵兩點 $a$ 同 $b$ 嚟睇，嗰兩點之間都可以有條獨一無二嘅直線將兩點連接埋一齊。

」

呢條公理唔成立。解說：想像下圖噉，下圖顯示咗個球體，攞個球體嘅「北極」 $T$ 同「南極」 $D$ 呢兩點嚟睇，呢兩點之間並冇一條「獨一無二嘅最短（經球體表面）直線距離」－例如有條線由 $T$ 經 $B$ 同 $L$ 去 $D$，又有條線由 $T$ 經 $A$ 同 $K$ 去 $D$，兩條線都係 $T$ 同 $D$ 之間嘅最短直線距離。噉即係話，歐氏幾何其中一條基本公理喺球面幾何當中唔成立，所以球面幾何係一套非歐幾里得幾何。喺廿一世紀初，非歐幾何相當重要，例如球面幾何喺針對天體嘅研究（例如天文學同導航呀噉）上就不可或缺。

除咗球面幾何，雙曲幾何亦都屬於非歐幾何。

其他領域

用坐標嚟想像三角形；個三角形每隻角都有個坐標值。

睇埋：複幾何、運算幾何同複幾何

以下係比較出名嘅幾何學子領域：

• 代數幾何同解析幾何：代數幾何嘅核心諗頭係要將幾何物體睇做代數方程嘅解；而解析幾何嘅核心諗頭就係用坐標研究幾何學；結合呢兩套幾何學，唔同嘅幾何物體可以想像成唔同嘅方程式，例如一條直線可以想像做

  $mx+b=y$

  $mx+b-y=0$（代數方程），

  • 當中 $(x,y)$ 係條線啲點嘅坐標值（用坐標），$m$ 會係條線嘅斜率，而 $b$ 會係條線同 Y 軸相交嗰點嘅 Y 坐標。再想像圓形，一個圓形响呢套幾何學上可以諗做個形條邊上面嘅每一點 $(x,y)$（用坐標）都會滿足

  $(x-a)^{2}+(y-b)^{2}=r^{2}$

  $(x-a)^{2}+(y-b)^{2}-r^{2}=0$（代數方程），

  • 當中 $(a,b)$ 係個圓心嘅坐標值，而 $r$ 係個圓形嘅半徑有幾長－用日常用語講，圓形就係「條邊上面每點都離圓心一樣咁遠」嘅幾何物體。代數幾何同解析幾何好有實用價值－自然科學同工程學等領域分析物體嘅形狀同郁動嗰時，就好興用代數同坐標嘅做法，例子可以睇吓牛頓力學同物理模擬等嘅課題。
• 微分幾何：用微積分同線性代數研究幾何學；喺好多現實應用當中，人都要計幾何物體嘅表面面積同體積，對於好似球體、錐體同立方體等簡單基本嘅幾何物體，佢哋嘅表面面積同體積可以用相對簡單嘅方程式計（睇返上面），但問題係現實世界嘅物體好少可會咁簡單，例子可以睇吓下圖噉嘅曲面－微分幾何就可以解決呢啲問題。微分幾何用咗微積分嘅做法：簡化講，微積分技術可以將一條曲線想像成一條無限咁多條極細直線組成嘅線，再用積分方法計出條線下面包含嘅面積，進而幫手計塊曲面包嘅體積。呢種噉嘅技術喺好多自然科學同工程學應用上都好有用。

• 拓撲學：想像家陣攞住件幾何物體，將件物體撳扁、拉長或者扭曲，途中唔准封件物體上面啲窿（會通過件物體嘅先算窿）、唔准開新窿、唔准撕爛件物體、唔准要件物體經過自己；
  • 啲噉嘅變化會改變件物體嘅某啲幾何特性，例如拉長就會改變件物體嘅長度，
  • 但又有啲特性係做咗噉嘅變化都唔會變嘅－假想有笪空間 $X$，$X$ 上面是但攞兩點 $x_{1},x_{2}$ 嚟睇，兩點之間都有路徑相通（睇埋路徑連通空間嘅概念），噉無論 $X$ 畀人點撳扁、拉長或者扭曲，佢都仲會有「上面是但攞兩點 $x_{1},x_{2}$ 嚟睇，兩點之間都有路徑相通」呢樣特性。簡化噉講，拓撲學就係想研究呢啲「無論件體點樣畀人撳扁、拉長或者扭曲，都唔會變」嘅幾何特性。

• 
  拓撲學諗嘅變形方式：
  將隻杯慢慢撳同拉，最後變成冬甩噉形。
• 

• 離散幾何：研究離散嘅幾何物體；「離散」係「連續」嘅相反，
  • 數學上講嘅連續可以想像成「有得斬件斬到幾細都得」，例如想像解析幾何下嘅一個 2D 圓形，分析者想設個圓形嘅圓心嘅坐標位置，個位置可以係 $(1,1)$，又可以係 $(1.01,1)$，又可以係 $(1.001,1)$，又可以係 $(1.0001,1)$－想像中嗰笪空間可以係噉斬件，而且無論斬到幾細，都仲有得再斬細啲，噉嘅空間係連續嘅；
  • 離散就唔同，想像家陣一位幾何學家想分析一拃波點樣疊埋一齊（上圖），當中假設啲波响成個過程裏面都唔會爛－即係話有得話疊波裏面「有 35 個波」但冇得話疊波裏面「有 35.5 個波」；研究呢啲離散幾何物體嘅，就係離散幾何。
  • 數學化嘅化學研究會用到離散幾何，因為原子就係離散嘅（可以睇吓原子論）。

應用

睇埋：應用數學

科學應用

睇埋：物理學、數理物理學、工程學、工程數學同自然形態規律

「數學係上帝用嚟編寫宇宙嘅語言。」 —伽利略

幾何學專諗點樣分析空間，而自然科學同工程學好多時都會或多或少噉用到空間相關嘅概念。

物理學好興將研究緊嘅物體當做幾何物體。

例如光學噉，光學顧名思義專研究光，而幾何光學往往會將光嘅前進想像成射線，並且用幾何學噉嘅方法分析光喺空間入面嘅移動，當中好出名嘅反射定律就係噉。想像下面附圖 1：家陣有條光線由 ${\text{P}}$ 點通過空氣（介質 1）前進，跟住射落去一塊鏡嘅表面（塊鏡表面嘅玻璃係介質 2），當條光線去到空氣同玻璃之間嘅位（${\text{O}}$）嗰時，條光線嘅一部份會變方向射返過去空氣（介質 1）嗰邊，射向 ${\text{Q}}$ 嘅方向；根據反射定律，當一條光射落去一塊表面嗰度嗰陣，反射嘅光同入射嘅光會成特定嘅角度；想像一條光線 ${\text{P}}$ 通過空氣射落去一塊鏡嗰度，射中塊鏡上面嘅點 ${\text{O}}$；反射定律講嘅係，反射嘅光線 ${\text{Q}}$ 同條法線（指同塊鏡嘅表面成垂直嘅線）會成角度 $\theta _{r}$，而且

$\theta _{r}=\theta _{i}$，

當中 $\theta _{i}$ 係 ${\text{P}}$ 同法線成嘅角度；簡單講，即係「反射角等於入射角」－淨係呢度已經用咗線同角度等嘅幾何概念。

附圖 1 附圖 1  喺實驗室入面展示反射嘅現象；量角器嘅量度清楚噉顯示 呢條定律講嘅嘢。 喺實驗室入面展示反射嘅現象；量角器嘅量度清楚噉顯示 $\theta _{r}=\theta _{i}$ 呢條定律講嘅嘢。  折射嘅展現；折射涉及一條光線介質改變（例如由通過空氣變成通過玻璃）嗰陣前進角度改變，而「角度會變幾多」可以用折射定律描述。 折射嘅展現；折射涉及一條光線介質改變（例如由通過空氣變成通過玻璃）嗰陣前進角度改變，而「角度會變幾多」可以用折射定律描述。

除咗光學之外，仲可以睇吓力學上對郁動嘅分析或者電磁學上對帶電荷物體嘅郁動嘅分析。機械工程等嘅工程學領域分析機械啲機件郁動嗰陣，亦都成日會將啲機件想像成幾何物體，會剖析啲機件之間嘅距離同角度，例子可以睇吓有關連桿機構嘅思考，亦都可以睇吓結構工程上成日用嘅結構分析。

藝術應用

耶路撒冷嘅圓頂清真寺係一棟畀好多人認為佢有美感嘅建築物，佢由側面睇高度同闊度（紅色框框）大致上成黃金比例。

睇埋：視覺藝術、構圖、黃金比例、花臣同數學之美

「冇咗數學，就唔會有藝術。」 —盧卡·帕西奧利

包括畫畫、雕塑、建築設計同演算法藝術在內嘅多門視藝，都會用到幾何學相關嘅概念。有學者指，好似畫畫噉嘅視藝本質上係喺空間當中編排顏色（相對於音樂係喺時間當中編排聲），必然會用到幾何學（研究空間嘅數學）嘅考量。

黃金比例（$\varphi$）可以話係幾何學藝術應用最出名嘅例子。有唔少藝術工作者同學者都認為，構圖上展示某啲數學特性嘅視藝作品會零舍有美感，而黃金比例呢個數值成日被指係同美感有重大關係：想像有兩個數值 $a$ 同 $b$，$a>b$；如果「$a+b$ 同 $a$ 之間嘅比例」等同「$a$ 同 $b$ 之間嘅比例」嘅話，$a$ 同 $b$ 就算係成黃金比例，即係話：

${\frac {a+b}{a}}={\frac {a}{b}}\ {\stackrel {\text{def}}{=}}\ \varphi$

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.6180339887\ldots .$

有好多藝術工作者相信，一件靚嘅視藝作品構圖上必需要喺某啲方面展示黃金比例；而文藝復興時期嘅意大利藝術家廣泛噉將黃金比例用喺佢哋作品嘅構圖當中，以達文西嘅作品《蒙娜麗莎》（1500 年代）為例：

黃金長方形嘅圖解；圖中嘅 同 成黃金比例。 黃金長方形嘅圖解；圖中嘅 $a$ 同 $b$ 成黃金比例。  《蒙娜麗莎》全圖 《蒙娜麗莎》全圖  蒙娜麗莎塊面俾人指係運用咗黃金長方形嘅原理。 蒙娜麗莎塊面俾人指係運用咗黃金長方形嘅原理。

除咗黃金比例，仲可以睇吓伊斯蘭建築－伊斯蘭建築出嗮名鍾意勁用幾何圖案。

簡史

15 世紀一幅圖畫；幅畫描繪歐洲同阿拉伯嘅學者一齊研究幾何學。

内文：幾何學史同幾何原本

幾何學早喺公元前 2,000 年嗰陣嘅兩河流域文明同古埃及已經存在。當時嘅人已經識得觀察周圍環境，得知長度、角度同面積等嘅概念，仲識用呢啲概念嚟做測量、建築施工同天文學等嘅工作，而且仲有寫文獻記低同教授幾何學知識，例如嚟自公元前 1850 年嘅莫斯科數學紙草書（一份古埃及紙草文獻）就有提供方程式計 3D 物體嘅體積。

古希臘係幾何學嘅一個黃金時期：古希臘哲學家畢達哥拉斯（公元前 580 - 500 年）證明咗畢氏定理，呢條定理到咗廿一世紀初係人都識咁滯，而且仲成日畀人攞去用；屬於幾何學基礎之一（兼史上歷史最悠久嘅教科書之一）嘅《幾何原本》就係出於大約公元前 300 年嘅，而喺呢本書入面歐幾里得引入咗公理等嘅概念，畀人指係確立咗幾何學嘅數學嚴謹性；除此之外，好出名嘅阿基米德亦都做咗唔少幾何學方面嘅研究，例如用當時前所未有咁高嘅準確度計出圓周率嘅確切數值呀噉。同期嘅印度亦都有出到唔少有睇頭嘅幾何學研究。

中世紀嗰陣嘅伊斯蘭世界有對幾何學作出咗貢獻（睇埋伊斯蘭黃金時期），尤其係代數幾何。例子可以睇吓波斯人數學家奧瑪開儼對一元三次方程同四邊形做嘅研究噉。

17 世紀嘅歐洲（睇埋啟蒙時期）出到好多重要發現，當中最出名嘅要數法國數學家笛卡兒同埋費馬發展出解析幾何－解析幾何用坐標分析幾何物體，畀人指係幫打後嘅微積分同精確物理學舖咗路。

非歐幾里得幾何嘅諗頭係喺 19 世紀出嘅。呢套幾何理論框架可以話係根本噉改變咗世人對幾何學嘅諗法，挑戰咗當時嘅好多根本假設－睇返上面講到，非歐幾何挑戰咗歐幾里得嗰幾條個個都覺得係啱嘅公理。

到咗廿一世紀初，幾何學已經成為咗科學同工程學工作當中不可或缺嘅知識：包括力學、光學、化學（可以睇吓對分子結構嘅研究）、建築設計、機械工程同埋電腦圖像等咁多唔同領域嘅工作，都會用到幾何學概念。

睇埋

• 向量同向量空間
• 物理學同相對論
• 時間同空間
• 測度
• 理型論
• 美學

參考

篇文用咗嘅行話、專有名詞或者名句，英文（或者其他外語）版本如下：

篇文引用咗以下呢啲文獻同網頁：

書目

英文書：

一覽

• • Boyer, C. B. (1991) [1989]. A History of Mathematics (Second edition, revised by Uta C. Merzbach ed.). New York: Wiley. ISBN 978-0-471-54397-8.
  • Bryant, J., & Sangwin, C. (2011). How round is your circle?. Princeton University Press.
  • Cooke, R. (2005). The History of Mathematics. New York: Wiley-Interscience. ISBN 978-0-471-44459-6.
  • Hayashi, T. (2003). "Indian Mathematics". In Grattan-Guinness, Ivor (ed.). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. Vol. 1. Baltimore, MD: The Johns Hopkins University Press. pp. 118-130. ISBN 978-0-8018-7396-6.
  • Hayashi, T. (2005). "Indian Mathematics". In Flood, Gavin (ed.). The Blackwell Companion to Hinduism. Oxford: Basil Blackwell. pp. 360-375. ISBN 978-1-4051-3251-0.
  • Kappraff, J. (2014). A Participatory Approach to Modern Geometry. World Scientific Publishing. doi:10.1142/8952. ISBN 978-981-4556-70-5.
  • Mlodinow, L. (2002). Euclid's Window - The Story of Geometry from Parallel Lines to Hyperspace (UK ed.). Allen Lane. ISBN 978-0-7139-9634-0.
  • Lobachevsky, N. I. (2010). Pangeometry. Heritage of European Mathematics Series. Vol. 4. translator and editor: A. Papadopoulos. European Mathematical Society.

外拎

• （英文） 幾何學，不列顛百科全書
• （英文） 幾何學，Wolfram 數學世界
• （英文） 幾何學當中嘅 Finitism，史丹福哲學百科全書