失蹤嘅正方形

失蹤嘅正方形嘅展示圖

將 A 重組變成 B

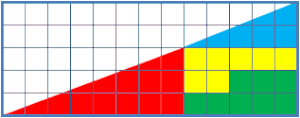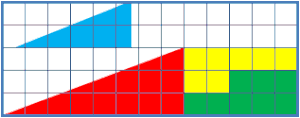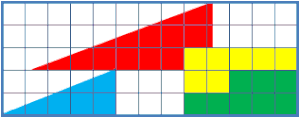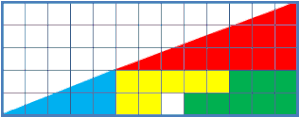
失蹤嘅正方形（英文：missing square puzzle）係幾何學上一條出名嘅謎題同視錯覺。想像附圖嗰兩個形狀 A 同 B，兩個形狀都係由幾塊彩色嘅板組成嘅，再考慮以下呢兩點：

• A 同 B 同樣都係由嗰幾塊板組成，所以理應係一樣面積嘅；不過
• 如果將 A 重組吓變做 B，就會發覺雖然 A 同 B 霸咗嘅空間都係都係 5 格咁高底邊 13 格咁長，但 B 有個「窿」－根據計三角形面積條方程式，B 同 A 比起嚟面積少咗格，有個正方形嘅格好似「失咗蹤」噉；

於是就引起咗條謎題。

解答

一般認為，呢條嘅答案在於一樣嘢：藍色嗰塊三角形板同紅色嗰塊查實並唔係相似嘅三角形；簡單噉講，如果將 A 同 B 呢兩個「三角形」嘅斜邊擺埋一齊睇（睇下圖），就會發覺 A 同 B 根本唔係真係三角形－兩個條斜邊都唔係完全嘅直線嚟嘅，所以計三角形面積嘅方程式理所當然唔會適用喺佢哋身上，不過 A 同 B 條斜邊同直線嘅偏差好細，就噉望落好似兩個條斜邊都係直線噉。

數學細節

要完整咁解釋點解會差咗1個格仔嘅話，就要證明埋上邊嗰個好窄嘅四邊形嘅面積係等於1格，呢個差異就造成咗個正方形「失蹤」嘅錯覺。證明嘅方法有幾種：

Pick定理

第一種係利用Pick定理（Pick's theorem），Pick定理係用嚟計算啲頂點全部喺格點上面嘅簡單多邊形嘅面積：

面積=內部格點+邊上格點÷2-1

套用呢個公式，個四邊形嘅面積就係$0+{\frac {4}{2}}-1=1$。

鞋帶公式

第二種係利用鞋帶公式（Shoelace formula）。個四邊形嘅四個頂點用逆時針順序座標分別係$(0,0),(8,3),(13,5),(5,2)$，代入鞋帶公式，四邊形嘅面積係：

${\frac {1}{2}}[(0\times 3-0\times 8)+(8\times 5-3\times 13)+(13\times 2-5\times 5)+(5\times 0-2\times 0)]=1$

同斐波那契數列嘅關係

失蹤嘅正方形，$8\times 21$版本

喺圖入邊所有出現嘅打直或者打橫嘅長度都係斐波那契數列入邊嘅數，例如紅色三角形嘅長闊係$3$、$8$，藍色三角形嘅長闊係$2$、$5$，成個形狀嘅長闊係$5$、$13$等等，事實上，換成其他斐波那契數列嘅組合，都可以得出類似嘅「失蹤嘅正方形」錯覺，右圖就係$8\times 21$嘅例子。

睇埋

• 視錯覺

拎

• 維基同享中有關失蹤嘅正方形嘅資源類