向量空間

上圖：向量加法，$\mathbf {v} +\mathbf {w}$：$\mathbf {v}$ 同 $\mathbf {w}$ 兩個向量加埋。
下圖：純量乘法， $2\cdot \mathbf {w}$：向量 $\mathbf {w}$ 乘 2 呢個純量；同埋向量加法，$\mathbf {v} +2\cdot \mathbf {w}$。

由 ${\text{O}}$ 去 ${\text{P}}$ 嘅位移可以想像成「$({\text{x}},{\text{y}},{\text{z}})$」呢個向量－「沿 ${\text{X}}$ 軸移 ${\text{x}}$ 咁遠、沿 ${\text{Y}}$ 軸移 ${\text{y}}$ 咁遠、沿 ${\text{Z}}$ 軸移 ${\text{z}}$ 咁遠」。

向量空間（粵拼：hoeng3 loeng6 hung1 gaan1；英文：vector space），又可以叫綫性空間（linear space），係指一個由「向量」組成嘅集合，當中呢啲向量可以加埋一齊（向量加法）或者俾純量乘大乘細（純量乘法）－簡單講，一個向量空間就係由好大拃向量結合形成嘅空間。向量空間有得按好多唔同嘅準則分類，例如係按照「乘得落啲向量度嘅純量係實數定虛數」分做實（real）向量空間同複（complex）向量空間噉，又可以按照上邊嘅額外結構分做代數、拓樸向量空間、巴那赫空間等等。

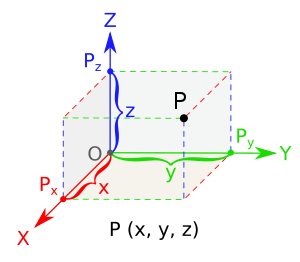
向量係由長度同方向組成嘅數學物體，喺三維空間（一般正常人類環境）嘅情況下，一個向量可以想像成包含咗三個數，表示個向量喺三條軸分別數值係幾多，例子：一個喺三維空間表示兩點之間嘅位移嘅向量會包含三個數 $(a_{1},a_{2},a_{3})$，三個數分別表示沿 X 軸嘅位移（$a_{1}$）、沿 Y 軸嘅位移（$a_{2}$）同沿 Z 軸嘅位移（$a_{3}$）。响物理學上，向量可以攞嚟表達好多物理量，例如牛頓力學上嘅分析就好興將位移同速度噉嘅物理量想像成向量。

因為向量咁有用，向量空間喺廿一世紀嘅數學、科學同工程學上係一樣重要嘅知識：向量空間係綫性代數（linear algebra）研究嘅基本對象，數學家會思考向量空間嘅數學特性，理解可以對向量作出點樣嘅運算，而呢啲研究得出嘅定理除咗滿足到理論性嘅好奇之外，仲有助科學家同工程師分析佢哋領域上遇到嘅問題。例如牛頓力學將位移同速度等嘅物理量想像成向量，並且靠呢啲概念分析物體點樣郁動，分析過程會用到數學上對「向量之間可以作出乜嘢運算」（向量空間研究會關注嘅一樣嘢）嘅知識，而呢啲力學分析跟手又對工程學有用，可以攞嚟分析汽車加速等嘅現象。

定義

喺呢篇文入面，大部分時候會用E, F, K代表一個場（field），V, W代表一個向量空間，a, b代表純量未知數，u, v, w代表向量未知數 。

用 $K$ 嚟表示一個場，場簡單嚟講即係做到加減乘除嘅數學結構，例如實數 $\mathbb {R}$ 、複數 $\mathbb {C}$ 、有限場$\mathbb {Z} _{p}$等。

一個 $K$-向量空間 ${\mathcal {V}}$ 就係一個三元組 ${\mathcal {V}}=(V,+,\cdot )$，當中：

• $V$ 係一個非空集，入面嘅元素叫做向量；
• $+:V\times V\to V$ 係一個函數，叫做向量加法；
• $\cdot :K\times V\to V$ 係另一個函數，叫做純量乘法。

佢哋要符合以下嘅條件：

1. $(V,+)$ 係一個阿貝爾羣（abelian group），即係話：
   1. $\exists \mathbf {0} \in V$ 令 $\mathbf {v} +\mathbf {0} =\mathbf {0} +\mathbf {v} =\mathbf {v} \quad \forall \mathbf {v} \in V$（存在加法單位additive identity）
   2. $\forall \mathbf {v} \in V\quad \exists (-\mathbf {v} )\in V$ 令 $\mathbf {v} +(-\mathbf {v} )=\mathbf {0}$（存在加法逆元additive inverse）
   3. $\mathbf {u} +(\mathbf {v} +\mathbf {w} )=(\mathbf {u} +\mathbf {v} )+\mathbf {w} \quad \forall \mathbf {u} ,\mathbf {v} ,\mathbf {w} \in V$（結合律）
   4. $\mathbf {u} +\mathbf {v} =\mathbf {v} +\mathbf {u} \quad \forall \mathbf {u} ,\mathbf {v} \in V$（交換律）
2. 純量乘法符合：
   1. $a\cdot (b\cdot \mathbf {v} )=(a\cdot b)\cdot \mathbf {v} \quad \forall a,b\in K\;\forall \mathbf {v} \in V$，當中左邊兩個點都係純量乘法，即係純量乘向量；右邊括號入面嗰點係場入面嘅乘法，即係純量乘純量。
   2. $1\cdot \mathbf {v} =\mathbf {v} \quad \forall \mathbf {v} \in V$，當中 $1$ 係場入面嘅乘法單位。
3. 分配性質：
   1. $a\cdot (\mathbf {v} +\mathbf {w} )=a\cdot \mathbf {v} +a\cdot \mathbf {w} \quad \forall a\in K\;\forall \mathbf {v} ,\mathbf {w} \in V$
   2. $(a+b)\cdot \mathbf {v} =a\cdot \mathbf {v} +b\cdot \mathbf {v} \quad \forall a,b\in K\;\forall \mathbf {v} \in V$

我哋同樣可以定義向量減法同純量除法，做法係透過逆元：

$\mathbf {u} -\mathbf {v} :=\mathbf {u} +(-\mathbf {v} )$

${\dfrac {\mathbf {u} }{a}}:={\dfrac {1}{a}}\mathbf {u}$

由上面嘅定義，可以推導出一啲常用嘅性質，例如一支向量 $\mathbf {v}$ 嘅加法逆元 $-\mathbf {v}$ 係唯一嘅；又或者 $a\mathbf {v} =0\iff a=0{\text{ or }}\mathbf {v} =0$，當中 $a$ 係純量，$\mathbf {v}$ 係向量，或者掉轉嚟講，非零純量同非零向量乘埋一齊唔會得到零向量。

歷史

向量空間嘅概念起源於仿射幾何學（affine geometry），透過喺二維同三維空間到用座標嚟表示啲點。大約 1636 年嗰陣，法國數學家笛卡兒同埋費馬透過聯繫二元方程式同埋平面曲線，爲分析幾何學奠基。喺 1804 年，爲咗唔用座標嚟得到幾何上嘅答案，Bolzano 引入咗一啲點、線同面上嘅一啲操作，呢個就係向量嘅前身。之後喺 1827 年莫比烏斯提出嘅重心座標（barycentric coordinates）亦都用到呢啲操作。向量嘅定義嘅基礎喺 Bellavitis 嘅「雙點記號」，佢係有向線段，一邊係原點，另一邊係目標點。之後，Argand 同 Hamilton 考慮用向量嚟表示複數同埋四元數（quaternion）。佢哋可以被睇做 $\mathbb {R} ^{2}$ 同 $\mathbb {R} ^{4}$ 入面嘅元素。

喺 1857 年，Cayley 引入矩陣記號，大大簡化咗線性映射嘅運算，喺同一段時間，Grassmann 研究莫比烏斯開創嘅重心演算，喺佢嘅成果入面，見到線性獨立、維度同埋純量乘法嘅概念。事實上 Grassmann 1844 年嘅成果唔單止包含向量，因爲佢仲考慮埋向量乘法，呢種結構依家叫做代數（algebra）。意大利數學家 Peano 喺 1888 年第一個畀出現代嘅向量空間同線性映射嘅定義。

向量空間一個好重要嘅發展係由 Henri Lebesgue 構作嘅函數空間，呢個概念喺大約 1920年由 Banach 同 Hilbert 正式定義；同一時間，代數同新興嘅泛函分析（functional analysis）開始互相影響，主要嘅發展有 p-可積函數同埋 Hilbert 空間；同一時期，數學家做咗初步嘅無限維向量空間嘅研究。

例子

座標空間

最簡單嘅 $K$-向量空間就係 $K$ 自己，當中向量加法同純量乘法分別係 $K$ 呢個場入面嘅加法同乘法；推廣一吓，畀定咗一個 $n\in \mathbb {N}$，所有 $n$ 元組 $(a_{1},\ldots ,a_{n})$ 形成咗一個 $n$ 維 $K$-向量空間，通常寫做 $K^{n}$，叫做座標空間，而 $(K,+,\cdot )$ 就係 $n=1$ 嗰陣嘅特例。當 $K=\mathbb {R}$ 同埋 $n=2$ 嗰陣我哋就得到平時熟悉嘅平面啦。

複數同場擴張

複數可以視爲一個實向量空間，當中：

• 向量加法：$(a+bi)+(c+di)=(a+c)+(b+d)i\quad \forall a,b,c,d\in \mathbb {R}$
• 純量乘法：$c\cdot (a+bi)=(ca)+(cb)i\quad \forall a,b,c\in \mathbb {R}$

好容易就可以檢查到佢哋啱返向量空間嘅公理。

事實上，只考慮 $\mathbb {R}$-向量空間嘅結構嘅話，$\mathbb {C}$ 同 $\mathbb {R} ^{2}$ 係「一樣」（同構）嘅，當中 $\mathbb {C}$ 入面嘅 $a+bi$ 對應 $\mathbb {R} ^{2}$ 入面嘅 $(a,b)$。

更一般嚟講，場擴張畀咗我哋好多向量空間嘅例子：假設 $F/E$ 係一個場擴張，噉 $F$ 就係一個 $E$-向量空間，向量加法同純量乘法都係用返 $F$ 入面嘅加法同乘法。例如 $\mathbb {C}$ 係一個 $\mathbb {R}$-向量空間，$\mathbb {Q} (i{\sqrt {5}})$ 係一個 $\mathbb {Q}$-向量空間。

函數空間

畀咗一個集合 $\Omega$，所有由 $\Omega$ 打去 $F$ 嘅函數組成一個 $F$-向量空間；又或者推廣一步，如果 $V$ 係一個 $F$-向量空間嘅話，所有由 $\Omega$ 打去 $V$ 嘅函數都會組成一個 $F$-向量空間，當中向量加法同純量乘法都係逐點逐點做嘅，即係話：

$(f+g)(x):=f(x)+g(x)\quad \forall x\in \Omega$

$(af)(x):=a(f(x))\quad \forall a\in F\;\forall x\in \Omega$

喺分析同幾何入面，個 $\Omega$ 可能係實數線、區間、拓樸空間或者流形入面嘅開集等等。

好多分析入面嘅性質，例如連續性、可積、可微，都會喺加法同埋純量乘法當中得到保留，所以呢啲函數組成嘅集會都係向量空間，例如：

• 區間 $[a,b]$ 上面嘅連續函數：$C[a,b]$
• 區間 $[a,b]$ 上面嘅連續可微函數：$C^{1}[a,b]$
• 區間 $[a,b]$ 上面嘅光滑函數：$C^{\infty }[a,b]$

基同維度

一支 $\mathbb {R} ^{2}$ 入面嘅向量 $v$ （藍色），用唔同嘅基嚟表示：用標準基嘅話，$v=xe_{1}+ye_{2}$（黑色），用另一個唔正交嘅基（）：）$v=f_{1}+f_{2}$（紅色）

基（basis）容許我哋用一個純量數列去表達啲向量，而啲純量就叫做座標或者分量。基係一個既可以生成成個空間而又係線性獨立嘅向量集 $B=\{b_{i}\}_{i\in I}$。生成成個空間指嘅係任何一支向量 $v$ 都可以寫做啲基向量嘅線性組合：

$v=a_{1}b_{i_{1}}+a_{2}b_{i_{2}}+\cdots +a_{n}b_{i_{n}}$

其中啲 $a_{k}$ 係純量，$b_{i_{k}}$ 係 $B$ 入面嘅向量。線性獨立（亦即係線性嘸相關）係指呢種寫法係唯一嘅，亦即係話呢啲 $a_{k}$ 只有一種選擇。

舉個例，喺 $F^{n}$ 入面我哋有一個基叫做標準基，佢係由 $e_{i}$ 組成，$i=1,2,\ldots n$：

${\begin{aligned}e_{1}&=(1,0,\ldots ,0)\\e_{2}&=(0,1,0,\ldots ,0)\\e_{n}&=(0,\ldots ,0,1)\end{aligned}}$

係噉任何向量 $(x_{1},x_{2},\ldots ,x_{n})$ 都可以唯一噉寫成佢哋個線性組合：

$(x_{1},x_{2},\ldots ,x_{n})=x_{1}(1,0,\ldots ,0)+x_{2}(0,1,0,\ldots ,0)+\cdots +x_{n}(0,\ldots ,0,1)$

其中，對應嘅 $x_{1},x_{2},\ldots ,x_{n}$ 就係笛卡兒座標。

喺 Zermelo-Fraenkel集合論入面，「任何向量空間都有最少一個基」係同選擇公理等價嘅，而通常會用另一個同選擇公理等價嘅Zorn's引理去證明任何向量空間都有基。超濾子引理（弱過選擇公理嘅假設）可以證明如果一個向量空間有唔同嘅基嘅話，呢啲基嘅基數係一樣嘅。呢個基數就得定義做向量空間嘅維度。如果個向量空間係由有限支向量生成嘅話，以上兩個結果唔需要選擇公理同埋超濾子引理，只需要 Zermelo-Fraenkel集合論就得。

由以上 $F^{n}$ 嘅基嘅例子可以睇到佢嘅維度係 n。多項式環 $F[x]$ 嘅維度係可數有限，其中一個基係 $1,x,x^{2},\ldots$。好多函數空間嘅例子似$C[a,b]$、$C^{1}[a,b]$、$C^{\infty }[a,b]$，佢哋嘅維度都係唔可數無限嘅。畀有一條齊次微分方程，如果啲系數夠光滑嘅話，解空間嘅維度同條微分方程嘅度數係一樣嘅，例如 $f''(x)+2f'(x)+f(x)=0$ 嘅解空間係由 $e^{-x}$ 同 $xe^{-x}$ 生成嘅二維函數空間。

上面提過，場擴張 $E/F$ 可以睇成 $E$ 係 $F$-向量空間，如果我哋考慮單擴張 $F(\alpha )/F$ 嘅話，佢嘅維度取決於 $\alpha$。如果 $\alpha$ 係 $F$ 上面嘅代數數嘅話，噉即係話 $\alpha$ 會符合一條最細多項式 $x^{n}+f_{n-1}x^{n-1}+\cdots +f_{0}=0$，當中 $f_{i}\in F$，噉 $F(\alpha )$ 嘅 $F$ 維度就係 $n$ 喇（$\dim _{F}(F(\alpha ))=n$）。舉個例，$\mathbb {C} =\mathbb {R} (i)$，而 $i$ 嘅最細多項式係 $x^{2}+1=0$，所以 $\dim _{\mathbb {R} }\mathbb {C} =2$。如果 $\alpha$ 唔係代數數嘅話，噉啫係佢係超越數，噉嘅話 $F(\alpha )\cong F(x)$，當中 $F(x)$ 係 $F$ 上面嘅有理函數，呢個情況個維度係可數無限嘅。

線性映射同矩陣

線性映射

畀咗兩個同一個場 $F$ 上面嘅向量空間 $V$ 同 $W$，我哋可以研究佢哋之間一啲保持向量空間結構嘅函數 $f:V\to W$；即係話，個函數 $f$ 保持 向量加法同純量乘法：

$f(v+w)=f(v)+f(w)$ 同埋 $f(av)=af(v)\quad \forall v,w\in V\;\forall a\in F$

$f:V\to W$ 得叫做向量空間同構（vector space isomorphism，或者簡單啲叫同構）若且唯若佢有一個反函數 $g:W\to V$ 令到兩個複合函數 $f\circ g$ 同 $g\circ f$ 都係恆等函數。等價嚟講，$f$ 要又係單射又係滿射。如果兩個向量空間 $V$ 同 $W$ 之間存在同構，我哋話佢哋係同構嘅，即係話呢兩個空間本質上係一樣嘅，因爲係 $V$ 入面嘅任何嘢我哋都可以用 $f$ 搬過去 $W$ 度講，又或者掉反轉用 $g$ 將 $W$ 入面嘅嘢搬嚟 $V$ 度講。

用 x,y 座標描述一個「箭嘴」，得到一個向量空間同構。

舉個例，「平面上面嘅箭嘴」同「實數二元有序對」係同構嘅，因爲畀咗個箭嘴你、喺固定嘅座標系統之下，可以度到佢嘅 x 部分同埋 y 部分（好似右圖噉）；掉反轉，畀咗兩個數 x 同 y 你，可以畫返個箭嘴出嚟，打橫 x 個單位，打直 y 個單位。

所有 $V\to W$ 嘅 $F$-線性映射形成咗一個向量空間 $\operatorname {Hom} _{F}(V,W)$，有時亦都寫做 $L(V,W)$。$V\to F$ 嘅所有線性映射形成嘅空間叫做 $V$ 嘅對偶空間，寫做 $V^{*}$。$V\to V^{**}$ 有個自然嘅單射：

$v\mapsto v^{**}:\forall f\in V^{*},v^{**}(f)=f(v)$

呢個單射將任意嘅向量空間嵌入佢嘅雙對偶空間入面，只有喺 $V$ 係有限維嗰陣呢個映射先會係一個同構。

如果 $V$ 有一個基，噉只要我哋知道呢個基嘅映像我哋就徹底瞭解到一個線性映射 $V\to W$，因爲 $V$ 入面任何一支向量都有唯一一種方法寫成基嘅線性組合。如果 $\dim V=\dim W$ ，而且 $V$ 同 $W$ 各自畀定一個基嘅話，基之間嘅一一對應關係就會伸延至一個 $V\to W$ 嘅線性映射，呢個映射會自動係一個同構。所以，兩個向量空間維度一樣嘅話佢哋就係同構嘅；掉反轉，同構嘅話維度一定一樣。另一個講法就係，向量空間可以用佢嘅維度去徹底分類（至同構）。舉個特例，任何 $n$-維向量空間 $V$ 都同 $F^{n}$ 同構，不過無一個自然、首選嘅同構；而事實上，揀一個同構 $F^{n}\to V$ 等同於幫 $V$ 揀一個基。

矩陣

一個矩陣

矩陣（matrix）係一個好方便嘅方法去描述一個線性映射，佢寫出嚟就係一個長方形陣列嘅數字，好似右圖噉。任何一個m乘n嘅矩陣都可以透過以下方法定義出一個$F^{n}\to F^{m}$嘅線性映射：

$x=(x_{1},x_{2},\ldots ,x_{n})\mapsto \left(\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\ldots ,\sum _{j=1}^{n}a_{mj}x_{j}\right)$

或者用矩陣乘法嘅話，$x\mapsto Ax$。另一方面，任意嘅線性映射 $f:V\to W$，只要幫 $V$ 同 $W$ 揀一個基，都可以用矩陣嘅形式去表達出來。

一個方形矩陣 $A$ 嘅行列式 $\det(A)$ 可以話畀我哋知某個對應嘅線性映射係唔係同構：佢係同構若且唯若行列式唔係 $0$。一個實向量空間上面嘅線性映射要保持定向，若且唯若佢嘅行列式係正數。

特徵值同特徵向量

自同態（endomorphism），指嘅係一個向量空間打返去自己度嘅線性映射 $f:V\to V$，佢哋有特別嘅意義，因爲一支向量 $v$ 可以同佢嘅映像 $f(v)$ 比較。任何一支向量 $v$ 如果符合 $f(v)=\lambda v$，當中 $\lambda$ 係純量嘅話，就叫做 $f$ 嘅一支特徵向量，而 $\lambda$ 就叫做特徵值。等價噉講，$v$ 係喺 $f-\lambda \cdot \operatorname {Id}$ 嘅核入面，當中 $\operatorname {Id} :V\to V$ 係恆等函數。如果 $V$ 係有限維嘅話，我哋可以用行列式嚟表達：$\lambda$ 係 $f$ 嘅特徵值若且唯若 $\det(f-\lambda \cdot \operatorname {Id} )=0$。如果將左邊嘅行列式展開嘅話，會得到一條 $\lambda$ 嘅多項式，叫做特徵多項式。如果個向量空間底下嗰個場係代數封閉嘅話，噉任何嘅自同態都一定至少有一支特徵向量。如果一個基入面所有向量都係特徵向量嘅話，個基就叫做一個特徵基。唔係所有自同態都有一個特徵基嘅；就算底下個場係代數封閉嘅都未必有。呢個現象可以用Jordan標準式嚟描述。畀咗一個特徵值，所有對應呢個特徵值嘅特徵向量會組成一個子空間，叫做特徵空間。無限維向量空間入面嘅特徵值分析叫做譜分析。

由舊嘅向量空間構作新嘅向量空間

子空間同商空間

一條穿過原點嘅藍線，佢係 $\mathbb {R} ^{3}$ 嘅子空間，係兩個平面嘅交集。

畀咗一個向量空間 $V$，佢嘅向量子空間（vector subspace，或者有時簡單啲，就噉叫子空間 subspace）係一啲喺向量加法同純量乘法下封閉嘅非空子集 $W$ ；因爲純量乘法嘅關係，佢自動會包埋 $0$-向量。子空間 $W$ 佢自己都係一個向量空間。畀一個 $V$ 嘅子集 $S$ （$S$ 唔一定要係子空間），所有裝住 $S$ 嘅子空間嘅交集都係一個子空間，叫做 $S$ 嘅生成空間，係最細包住 $S$ 嘅子空間。用元素嚟講嘅話，佢由 $S$ 入面嘅元素嘅線性組合構成。

一個一維嘅子空間叫做線，二維嘅就叫平面。注意有時呢個名會同我哋嘅直覺一啲出入，例如「複數線」指嘅係一維嘅複數空間 $\mathbb {C} ^{1}$，但係好多時啲人會用實數嚟諗，覺得 $\mathbb {C} ^{1}$ 應該係一個平面。低過主空間一維嘅子空間叫做超平面；另一個講法係對應嘅商空間（見下）係一維嘅；仲有第三個講法，係話呢個空間嘅餘維度係 $1$。

同子空間相對嘅概念係商空間。畀任何一個子空間 $W\subset V$，商空間 $V/W$ 係噉定義嘅：作爲一個集合，佢嘅元素係 $v+W=\{v+w:w\in W\}$，當中 $v\in V$ 係任意嘅向量。加法嘅定義係 $(v_{1}+W)+(v_{2}+W)=(v_{1}+v_{2})+W$，乘法係 $\alpha (v+W)=(\alpha v)+W$。係呢個定義入面一個好重要嘅觀察係 $v_{1}+W=v_{2}+W\Longleftrightarrow v_{1}-v_{2}\in W$。概念上，商空間就係忘記 $W$ 入面嘅資訊。呢個觀察亦都證明咗以上加法同乘法都係良定義嘅。

畀一個線性映射 $f:V\to W$ ，有幾個相關嘅子空間同商空間。第一個係核 $\ker(f)=\{v\in V|f(v)=0\}$，佢係 $V$ 嘅子空間；第二個係映像 $\operatorname {im} (f)=\{f(v):v\in V\}$，佢係 $W$ 嘅子空間；第三個係餘核 $\operatorname {coker} (f)=W/\operatorname {im} (f)$，係佢 $W$ 嘅商空間。證明向量空間範疇係阿貝爾範疇需要用到呢幾個空間嘅存在性；都因爲噉，好多相關嘅定理係呢個範疇都係啱嘅，例如第一同構定理 $V/\ker(f)\cong \operatorname {im} (f)$，同埋其他同構定理等等。

直和同直積

畀有一柞向量空間$(V_{i})_{i\in I}$，可以用兩種方法去結合呢柞向量空間，整個新嘅向量空間出嚟。

首先係直積$\prod _{i\in I}V_{i}$（direct product），佢包含住所有啲多元組 $(v_{i})_{i\in I}$，當中對於每一個 $i\in I$ 都有 $v_{i}\in V_{i}$，向量加法同埋純量乘法都係逐項逐項做嘅。

另一方面，直和 $\bigoplus _{i\in I}V_{i}$ （direct sum）係直積嘅子空間，只包含嗰啲多元組「只有有限項唔係0向量」嘅；如果 $I$ 係有限嘅話，兩個構作係一樣嘅，但係如果 $I$ 係無限嘅話就唔同喇。

另外，直積同直和分別係向量空間範疇入面嘅積（product）同餘積（coproduct）。

張量積

展示張量積萬有性質嘅交換圖。

兩個 F-向量空間 $V$ 同 $W$ 嘅張量積（tensor product） $V\otimes _{F}W$（或者如果好清楚係邊個場嘅話可以唔寫：$V\otimes W$）係喺多重線性代數入面一個好重要嘅構作。一個映射 $g:V\times W\to X$ 叫得做雙線性若且唯若佢對兩個輸入都係線性嘅；即係話，固定一個 $w$，$v\mapsto g(v,w)$ 係線性映射，反之亦然。

張量積 $V\otimes W$ 係雙線性映射嘅「萬有物件」，佢係以下形式嘅「張量和」組成嘅向量空間：

$v_{1}\otimes w_{1}+v_{2}\otimes w_{2}+\ldots v_{n}\otimes w_{n}$ （n 係任意正整數，$v_{i}\in V$，$w_{i}\in W$）

當中 $\otimes$ 運算符合以下規則：

$a\cdot (v\otimes w)=(a\cdot v)\otimes w=v\otimes (a\cdot w)\quad \forall a\in F,v\in V,w\in W$

$(v_{1}+v_{2})\otimes w=v_{1}\otimes w+v_{2}\otimes w\quad \forall v_{1},v_{2}\in V,w\in W$

$v\otimes (w_{1}+w_{2})=v\otimes w_{1}+v\otimes w_{2}\quad \forall v\in V,w_{1},w_{2}\in W$

呢啲規則確保咗 $f:V\times W\to V\otimes W$，$f(v,w)=v\otimes w$係雙線性嘅。萬有性質係指對任何雙線性映射 $g:V\times W\to X$，都有一個唯一嘅線性映射 u 符合 $g=u\circ f$，亦即係令到右圖係「交換」嘅。呢一種用萬有性質嚟定義物件嘅做法喺抽象代數入面係好常見嘅。

額外結構

賦範向量空間同內積空間

本身一個向量空間入面，我哋係冇得講出一支向量嘅「長度」嘅，但係如果向量空間有一個範數（norm）定義咗嘅話就可以喇；而如果向量空間有定義到內積（inner product）嘅話，我哋甚至可以講出向量之間嘅角度。通常會用$|v|$ 同 $\langle v,w\rangle$ 嚟表示範數同埋內積；而如果一個向量空間上面有內積嘅話，就可以定義一個自然嘅範數：$|v|:={\sqrt {\langle v,v\rangle }}$。呢啲有額外結構嘅向量空間就分別叫做賦範向量空間同埋內積空間喇。

對任何正整數 n 同埋實數 p>1，可以定義賦範向量空間 $F_{p}^{n}(F=\mathbb {R} {\text{ or }}\mathbb {C} )$：

$|(x_{1},\ldots ,x_{n})|={\sqrt[{p}]{|x_{1}|^{p}+\ldots +|x_{n}|^{p}}}$

對任何正整數 n，可以定義內積空間 $F^{n}(F=\mathbb {R} {\text{ or }}\mathbb {C} )$：

$\langle x,y\rangle =x_{1}{\bar {y_{1}}}+\ldots +x_{n}{\bar {y_{n}}}$

係 $\mathbb {R} ^{2}$ 入面，我哋有餘弦公式：

$\cos(\angle (x,y))={\dfrac {x\cdot y}{|x||y|}}$

所以喺其他內積空間，我哋可以用呢條式去推廣角度嘅定義；x 同 y 正交若且唯若 $\langle x,y\rangle =0$。內積空間有一個好重要嘅變體，叫做Minkowski時空：$\mathbb {R} ^{4}$，賦予 Lorentz積：

$\langle x|y\rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}$

同內積唔同，Lorentz積唔係正定嘅：$\langle x|x\rangle$ 可以係負數，例如 $x=(0,0,0,1)$。將第四個座標睇做時間，頭三個睇做空間，噉樣可以睇得出個 Minkowski時空對狹義相對論嘅數學運算好有幫助。

拓撲向量空間

喺一個向量空間入面，定義咗點樣將兩支向量加埋一齊；佮埋加法嘅結合性質，可以定義點樣將有限支向量加埋一齊：可以定義$\sum _{i=1}^{n}v_{i}=v_{1}+\left(\sum _{i=2}^{n}v_{i}\right)$，因爲有結合性質，加咗邊兩支先係無分別嘅：

$v_{1}+(v_{2}+(v_{3}+v_{4}))=((v_{1}+v_{2})+v_{3})+v_{4}=(v_{1}+v_{2})+(v_{3}+v_{4})$

但係講到話想加埋無限支向量，噉個向量空間就一定要有一個拓撲結構喇，因爲噉先可以講級數嘅收斂性。一般我哋都要求呢個拓撲結構同向量加法同埋純量乘法係相容嘅；粗略噉講，如果 $u,v\in V,a\in F$ 改變少少嗰陣，$u+v,av$ 都唔應該改變太多。想描述純量嘅改變嘅話，個場 $F$ 都要有一個拓撲結構，即係話 $F$ 係一個拓撲場。好多時 $F$ 都係 $\mathbb {R}$ 或者 $\mathbb {C}$ ，帶住平時嗰個拓撲結構。

噉樣喺拓撲向量空間入面，我哋可以講一個級數嘅收斂性：定義$\sum _{i=0}^{\infty }v_{i}$ 做 $\lim _{n\to \infty }\sum _{i=0}^{n}v_{i}$ （如果收斂嘅話），例如 $v_{i}$ 可以係某個函數空間入面嘅函數；噉嘅情況呢個級數就係函數級數，收斂模式同向量空間嘅拓撲結構有關，例如逐點收斂同一致收斂對應住唔同嘅拓撲結構。

$\mathbb {R} ^{2}$ 入面唔同嘅 p-範數之中嘅「1-球體」$\{x{\Big \vert }|x|=1\}$，最大黃色嗰個係 1-範數入面嘅「2-球體」。

一個確保向量空間有足夠多嘅極限嘅方法係淨係考慮某一種空間，佢嘅柯西列一定有極限；呢種向量空間叫做完備。舉個例，單位區間 [0, 1] 上面嘅多項式函數組成一個向量空間，如果佢帶住一致收斂拓撲嘅話，佢就係唔完備嘅，因爲根據 Stone-Weierstrass定理所有 [0, 1] 上面嘅連續函數都可以由多項式函數一致噉逼近。相反，[0, 1] 上面嘅連續函數就係一個完備空間喇。一個賦範向量空間會自動帶有一個拓撲結構，定義係 $v_{n}\to v\Leftrightarrow |v_{n}-v|\to 0$。

Banach空間同Hilbert空間係完備嘅拓撲向量空間，佢哋嘅拓撲結構分別係由範數同埋內積帶嚟嘅。泛函分析入面我哋會研究呢兩種空間，主要研究無限維空間，因爲有限維上面所有範數畀嘅拓撲結構都係一樣嘅，所有數列嘅收斂條件都係一樣嘅。右圖展示出 1-範數同 $\infty$-範數係等價嘅：$\infty$-範數嘅「1-球體」包住 1-範數嘅「1-球體」，而 1-範數嘅「2-球體」又包返住$\infty$-範數嘅「1-球體」，即係展示出佢哋嘅拓撲結構係一樣嘅。喺無限維入面，一般嚟講會有好多種唔同嘅拓撲結構，例如 $L^{p}(\mathbb {R} )$ 同 $L^{q}(\mathbb {R} )(p\neq q)$ 係唔同嘅，所以研究呢啲唔同嘅拓撲係一個有趣嘅課題。

概念上嚟講，所有同拓撲向量空間有關嘅概念都應該同個拓撲結構係相容嘅；例如考慮線性映射嗰陣，我哋會考慮拓撲向量空間之間嘅連續線性映射。舉個特例，拓撲對偶空間 $V^{*}$ 係所有 $V\to \mathbb {R}$（或者$\mathbb {C}$）嘅連續線性映射（或者叫連續泛函）。Hahn-Banach定理係泛函分析入面嘅一條基礎定理，展示出任何嘅賦範向量空間入面都有足夠嘅泛函畀我哋去研究。

Banach空間

Banach空間（Banach space）由 Stefan Banach 定義，亦都因爲噉以佢嚟命名，係指完備嘅賦範向量空間。

第一個例子係 $\ell ^{p}$ 空間。首先對無限向量 $x=(x_{0},x_{1},\ldots )$ 定義 p-範數（場係 $\mathbb {R}$ 或 $\mathbb {C}$，$1\leq p\leq \infty$）：

$p<\infty$ 嘅話 $||x||_{p}:=\left(\sum _{i}|x_{i}|^{p}\right)^{\frac {1}{p}}$，$||x||_{\infty }=\sup _{i}|x_{i}|$

$\ell ^{p}$ 空間就係由有有限 p-範數嘅向量組成嘅向量空間。

對於唔同嘅 p ，$\ell ^{p}$ 空間嘅拓撲係唔同嘅，例如 $x_{n}=(\underbrace {2^{-n},2^{-n},\ldots ,2^{-n}} _{2^{n}},0,0,\ldots )$ 就同時喺 $\ell ^{\infty }$ 同埋 $\ell ^{1}$ 空間入面。但係喺 $\ell ^{\infty }$ 入面佢嘅極限係 0 向量，而喺 $\ell ^{1}$ 入面佢就唔收斂：

$\left\Vert \mathbf {x} _{n}\right\Vert _{_{\infty }}=\sup(2^{-n},0)=2^{-n}\rightarrow 0$，但 $\left\Vert \mathbf {x} _{n}\right\Vert _{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1$

推而廣之，如果 $\Omega \subset \mathbb {R} ^{n}$ 係一個區域，上面有 Lebesgue 積分，噉我哋可以定義一個 p-範數：

$\left\Vert {f}\right\Vert _{p}:=\left(\int _{\Omega }\left\vert {f}\left(x\right)\right\vert ^{p}\,{d\mu \left(x\right)}\right)^{\frac {1}{p}}$

$L^{p}(\Omega )$ 就係由有有限 p-範數嘅函數組成嘅向量空間，叫做 Lebesgue空間。呢啲空間係完備嘅（如果用 Riemann積分就唔完備，呢個亦係其中一個原因高等數學分析要用 Lebesgue積分，唔用 Riemann積分）。

完備嘅意思即係，對任何 $L^{p}(\Omega )$入面嘅函數列 $f_{1},f_{2},\ldots ,f_{n},\ldots$，$||f_{n}||_{p}<\infty$，並符合 Cauchy條件：

$\lim _{k,\ n\to \infty }\int _{\Omega }\left\vert {f}_{k}(x)-{f}_{n}(x)\right\vert ^{p}\,{d\mu \left(x\right)}=0$

都存在一個函數 $f\in L^{p}(\Omega )$ 令到

$\lim _{k\to \infty }\int _{\Omega }\left\vert {f}\left(x\right)-{f}_{k}\left(x\right)\right\vert ^{p}\,{d\mu \left(x\right)}=0$

如果我哋唔單止要求函數係有界嘅，仲要求埋佢嘅導數都係有界嘅，噉我哋就得到 Sobolev空間喇。

Hilbert空間

用正弦函數嘅有限和（紅色）嚟逼近三角波（藍色）嘅頭五項。

Hilbert空間以 David Hilbert 命名，指嘅係完備嘅內積空間，一個重要例子係 $L^{2}(\Omega )$，內積係

$\langle f,g\rangle =\int _{\Omega }f(x){\overline {g(x)}}\mathrm {d} x$

當中條橫線代表複共軛。

根據定義，喺 Hilbert空間入面所有 Cauchy 數列都會收斂到某一向量；掉反轉，用一個有某一性質嘅數列去逼近一支冇呢個性質嘅向量都係好重要嘅概念嚟。係早期分析入面，用 Taylor展開我哋可以用多項式嚟逼近可微函數；根據 Stone-Weierstrass定理，任何 [a, b]上嘅連續函數都可以用多項式嚟逼近。用三角函數嚟逼近就係 Fourier分析入面研究嘅嘢，對工程學好有用。更一般、更抽象嚟講，呢啲定理係描述緊一啲基。喺 Banach空間或者 Hilbert空間入面，一個集叫得做基若且唯若佢嘅生成空間嘅閉包係成個空間。由於 Hilbert空間有定義到內積，配合埋 Gram-Schmidt過程，我哋可以構作 Hilbert空間嘅正交基。

好多微分方程嘅解都可以用 Hilbert空間嚟描述；例如物理入面，量子力學入面嘅時間無關Schrödinger等式用偏微分方程嚟描述一啲物理值隨時間嘅改變，啲解叫做波函數。某啲物理性質（例如能量、動量）嘅值對應住某啲算子嘅特徵值，而對應嘅特徵函數就係狀態函數。譜定理可以將緊緻算子分解成呢啲特徵函數上面嘅作用。

場上代數

$xy=1$所表示嘅雙曲線，佢嘅座標環係 $\mathbb {R} [x,y]/(xy-1)$，一個無限維嘅實向量空間。

一般嘅向量空間係冇定義點樣將兩支向量乘埋嘅，而如果有嘅話（而且符合一啲相容性嘅公理）就叫做一個場上代數（algebra over a field），或者就噉代數。好多代數係嚟自一啲幾何物體上邊嘅函數，因爲呢啲函數可以逐點逐點乘埋一齊。例如 Stone-Weierstrass 定理就係同 Banach 代數有關嘅，啫係佢又係代數又係 Banach空間。

交換代數入面成日都會研究單參數或者多參數嘅多項式環，佢哋嘅乘法係交換同埋結合嘅；呢啲環同埋佢哋嘅商係研究代數幾何嘅基本部分，因爲佢哋就係幾何物件上面嘅函數空間。

另一個例子係李代數，佢嘅乘法（一般叫做李括號）又唔交換又唔結合，但係要求符合另外兩條式（$[x,y]$ 表示 $x$ 同 $y$ 嘅乘積）：

• $[x,y]=-[y,x]$ （反交換律）
• $[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0$ （Jacobi等式）

例子包括對於 $n\times n$ 矩陣，李括號就係交換子 $[x,y]=xy-yx$（右邊係普通矩陣乘法）；同埋對於 $\mathbb {R} ^{3}$，李括號係外積。

張量代數係一個形式上嘅方法將任何嘅向量空間變成一個代數嘅。作爲一個向量空間，佢係由「簡單張量」（或者叫「純張量」）$v_{1}\otimes v_{2}\otimes \ldots \otimes v_{n}$ 生成嘅（$n$唔係固定嘅），而乘法就係將佢哋「連埋一齊」：

$(v_{1}\otimes v_{2}\otimes \ldots \otimes v_{n})\otimes (u_{1}\otimes u_{2}\otimes \ldots \otimes u_{m})=v_{1}\otimes v_{2}\otimes \ldots \otimes v_{n}\otimes u_{1}\otimes u_{2}\otimes \ldots \otimes u_{m}$

並且要求佢同純量乘法同向量加法相容。一般嚟講$v_{1}\otimes v_{2}$同$v_{2}\otimes v_{1}$係冇關係嘅，如果（透過取商）要求佢哋一樣嘅話，就得到對稱代數；而如果要求$v_{1}\otimes v_{2}=-v_{2}\otimes v_{1}$嘅話，噉就得到外代數。

有時我哋會叫 F 上嘅代數做 F-代數。

應用

分佈

一個分佈（distribution，或者廣義函數）係一個連續線性映射，畀一個「測試函數」佢、佢會畀返個數字你嘅，當中個測試函數通常係一個光滑函數，而且係緊支撐嘅。用返上面嘅術語，分佈空間係測試函數空間嘅連續對偶空間，當中測試函數空間上面嘅拓撲唔單止反映緊 $f$ 嘅性質，仲考慮埋 $f$ 嘅微分嘅性質。一個典型分佈嘅例子係將測試函數對某個區域 $\Omega$ 積分：

$I(f)=\int _{\Omega }f(x)\mathrm {d} x$

如果 $\Omega =\{p\}$ 只係一點嘅話，呢個分佈就係 Dirac分佈，通常用 $\delta$ 嚟表示：$\delta (f)=f(p)$。分佈係解微分方程好有用嘅工具：由於好多微分方程入面嘅算子都係線性嘅，例如微分噉，所以佢哋可以延伸去分佈空間上面；而分佈空間大過函數空間，所以有多啲工具去處理佢哋。例如 Green's函數同埋基礎解好多時都只係分佈而唔係函數，但係佢哋可以用來搵一啲邊值問題嘅解；而有啲情況噉樣搵出嚟嘅解唔單止係分佈，仲係函數嚟添，噉佢就係原本條問題嘅解。

Fourier分析

熱方程式描述一啲物理性質隨時間嘅擴散，例如擺一件熱嘅物體喺凍嘅環境入面嗰陣溫度嘅變化。（圖入面黃色代表凍，紅色代表熱）

將一個週期函數分解做三角函數就形成咗 Fourier級數，係一個喺物理同工程學入面好常見嘅技巧。底下嘅 Hilbert空間通常係 $L^{2}(\mathbb {T} )$（$\mathbb {T}$係複平面入面嘅單位圓），喺入面函數 $\sin mx$ 同 $\cos mx$ （m 係整數）係一套正交基底。一個 $L^{2}$函數 $f$ 嘅 Fourier展開係：

$\displaystyle {\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }[a_{m}\cos(mx)+b_{m}\sin(mx)]$

a_m同b_m叫做 f 嘅 Fourier係數，可以用以下嘅公式計出嚟：

$a_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\cos(mt)\,dt$, $b_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\sin(mt)\,dt.$

用物理學嘅術語嚟講，即係拆開咗呢個函數變成正弦函數同餘弦函數嘅疊加，而啲Fourier係數就畀咗個函數喺頻譜方面嘅資訊。Fourier級數有實數同複數兩個版本，兩個都咁常用。呢一個計算Fourier係數嘅方程式其實可以推廣去一個抽象嘅數學對偶概念，叫 Pontryagin對偶；喺Pontryagin對偶入面，整數羣$\mathbb {Z}$ 同圓羣$\mathbb {T}$ 係相對嘅。

Fourier級數可以用嚟解偏微分方程之中嘅邊值問題。1822年，Fourier首次用呢個方法嚟解啲熱方程式。Fourier級數嘅離散版本可以用嚟對函數取樣：我哋淨係知道個函數喺有限個間隔相同嘅點上面嘅數值，呢個情況Fourier級數係有限和，而加出嚟嘅值喺嗰啲取樣點上面係吻合翻個函數嘅；呢啲係數就叫做離散Fourier變換（英文：discrete Fourier transform，DFT）。DFT係電子訊號處理嘅一個主要工具，喺雷達、語音編碼同圖片壓縮方面好有用。JPEG格式就係離散餘弦變換嘅一個應用，係同離散Fourier變換好類似嘅一個變換。

快速傅立葉變換係用嚟計離散傅立葉變換嘅一個好快嘅演算法。佢唔單止可以用嚟計傅立葉係數，而且因爲有卷積定理，可以用嚟計一啲有限數列嘅卷積，所以可以用喺數字濾波器同埋多項式、大數字嘅快速乘法（Schönhage–Strassen演算法）。

微分幾何

2-球體喺一點上面嘅切平面

喺一幅曲面上面，一點嘅切平面（tangent space）係一個向量空間，當中個原點對應住切平面同曲面嘅接觸點嘅。切平面係喺嗰一點附近，對幅曲面最好嘅線性近似。就算係嵌入咗三維空間入面嘅曲面，一般嚟講切平面都係無一個特別嘅、優先嘅基嘅，所以切平面一般都係用一個抽象嘅向量空間嚟描述，而唔係一個實向量空間 $\mathbb {R} ^{2}$。而切空間就係將呢一個概念推廣去更高維嘅可微流形上面。

黎曼流形係一種可微流形，上面每一個切空間都有一個適當嘅內積；由呢個內積可以計算出黎曼曲率張量，佢蘊含住成個流形每一點嘅曲率資訊，對廣義相對論好有用，例如愛因斯坦曲率張量描述咗時空入面嘅能量同埋質量。

另外，李羣入面嘅切空間好自然噉形成咗一個李代數，可以用嚟分類緊緻李羣。

推廣

（無限延長嘅）莫比烏斯帶係圓$S^{1}$上嘅一個向量叢，局部嚟睇，每一點附近佢都好似直積 $U\times \mathbb {R}$，但係成個空間就唔係直積 $S^{1}\times \mathbb {R}$。

向量叢

向量叢（vector bundle）係以空間上嘅點嚟參數化嘅一堆向量空間 。或者噉講，對任何拓撲空間${\mathcal {M}}$（通常係一個流形）同向量空間$V$，我哋可以整一個積空間${\mathcal {M}}\times V$；上面我哋攞積拓撲，而向量叢就係呢個概念嘅推廣。向量叢可以理解做扭曲咗嘅積空間。具體嘅定義係，拓撲空間${\mathcal {M}}$上嘅向量叢係一個拓撲空間$E$，連同一個連續映射（理解做投影）：

$\pi :E\to {\mathcal {M}}$

令到對每一點$x\in {\mathcal {M}}$，佢嘅纖維$\pi ^{-1}(x)$都係一個向量空間$V$。如果$V$嘅維度係1嘅話，會叫佢做線叢（英文：line bundle）。上一段講嘅積空間都係向量叢嘅一種，叫平凡向量叢（英文：trivial bundle）。此外，一般嚟講數學家都要求向量叢係局部平凡嘅；亦即係話，對任何一點$x\in {\mathcal {M}}$，都有一個鄰域$x\in U\subset {\mathcal {M}}$，令到$(\pi ^{-1}(U),\pi )$係同平凡向量叢$U\times V\to U$同構嘅。就算向量叢係局部平凡都好，整體來講亦都可以係「扭曲」嘅；意思即係，成個向量叢$E$同$U\times V$唔一定係同構。最簡單嘅例子就係莫比烏斯帶，佢可以睇做圓上面嘅一個向量叢，但係佢同圓柱體（$S^{1}\times \mathbb {R}$）係唔同構嘅，因爲圓柱體係可定向嘅，莫比烏斯帶唔係。

某啲向量叢（譬如切線叢）嘅性質可以調返轉頭話畀我哋知底下個拓撲空間嘅性質。切線叢係將可微流形上嘅每一點嘅切空間黐埋一齊，例如圓形$S^{1}$嘅切線叢係同$S^{1}\times \mathbb {R}$同構嘅（即係平凡嘅），因爲$S^{1}$上面存在每點都唔係零嘅向量場。相反，根據毛球定理，2-球面$S^{2}$上面任何嘅向量場都一定有零點，即係話$S^{2}$嘅切線叢係唔平凡嘅。K-理論就係研究一個空間上面所有向量叢嘅同構類嘅。向量叢除咗加深咗對拓撲學同埋幾何學嘅理解之外，亦都對純代數有影響，例如證明咗有限維實除代數只有4種：實數$\mathbb {R}$、複數$\mathbb {C}$、四元數$\mathbb {H}$同八元數$\mathbb {O}$。

除咗切線叢，仲可以定義餘切叢（英文：cotangent bundle），佢係將每一點上面嘅切空間嘅對偶（餘切空間）黐埋一齊，呢個叢上面嘅截面叫做1-微分形式。

模

模（module）係環版本嘅向量空間，意思即係，喺向量空間入面，將場 $F$ 換做環 $R$ 就得到 $R$-模嘅定義喇。模嘅理論複雜過向量空間，因爲 $R$ 入面有啲無乘法逆元嘅元素。舉個例，有啲模係無基嘅，例如 $\mathbb {Z}$-模（等價於阿貝爾羣）$\mathbb {Z} /2\mathbb {Z}$ 噉。有基嘅模叫做自由模。

仿射空間同投影空間

$\mathbb {R} ^{3}$入面嘅一個仿射平面（淺藍），佢係由一個子空間平移咗$x$（紅）咁多得出嚟。

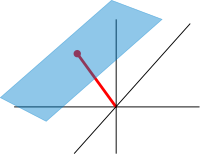
粗略來講，仿射空間就係唔記得咗原點喺邊嘅向量空間，所以喺上面係冇得做加法嘅。準確啲嚟講，仿射空間係一個集合，上面有一個向量空間嘅自由遞移作用。噉睇嘅話，任何向量空間$V$都係一個仿射空間，因爲有呢一個作用：

$V\times V\to V,(v,a)\mapsto a+v$

如果$V$係一個向量空間嘅話，佢嘅仿射子空間可以透過將佢一個向量子空間$W$沿住一支揀定咗嘅向量$x$平移嚟得到，呢個空間會記作$x+W$（佢係$V$入面$W$嘅一個陪集），佢包含住所有$x+v$噉嘅樣嘅向量，當中$v$係$V$入面嘅向量。一個重要嘅例子就係非齊性線性方程式$Ax=b$嘅解，個解空間係$x+V$，當中$x$係一個特別解，$V$就係對應齊性方程$Ax=0$嘅解空間，亦即係$A$嘅核。

揀定一個向量空間$V$，佢嘅所有一位子空間形所咗一個空間，叫做投影空間；呢個空間可以用嚟展示平行線相交於無限處嘅概念。Grassmannian同埋旗流形係呢個概念嘅推廣，佢哋分別係子空間同埋子空間旗嘅參數化。

睇埋

• 向量
• 模
• Riesz–Fischer定理
• 空間 (數學)
• 有序向量空間

書目

代數

• Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-89871-510-1
• Blass, Andreas (1984), "Existence of bases implies the axiom of choice", Axiomatic set theory (Boulder, Colorado, 1983), Contemporary Mathematics,第31卷, Providence, R.I.: American Mathematical Society, pp. 31–33, MR 0763890
• Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
• Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
• Lang, Serge (2002), Algebra, Graduate Texts in Mathematics,第211卷 (第Revised third版), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
• Mac Lane, Saunders (1999), Algebra (第3版), pp. 193–222, ISBN 978-0-8218-1646-2
• Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, SIAM, ISBN 978-0-89871-454-8
• Roman, Steven (2005), Advanced Linear Algebra, Graduate Texts in Mathematics,第135卷 (第2版), Berlin, New York: Springer-Verlag, ISBN 978-0-387-24766-3
• Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups, CRC, ISBN 978-0-8247-9144-5
• van der Waerden, Bartel Leendert (1993), Algebra (德文) (第9版), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56799-8

分析

• Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-13627-9
• Bourbaki, Nicolas (2004), Integration I, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41129-1
• Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97894-9
• BSE-3 (2001), "Tangent plane", 出自 Hazewinkel, Michiel (編), Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
• Choquet, Gustave (1966), Topology, Boston, MA: Academic Press
• Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists, Courier Dover Publications, ISBN 978-0-486-69193-0
• Dudley, Richard M. (1989), Real analysis and probability, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6
• Dunham, William (2005), The Calculus Gallery, Princeton University Press, ISBN 978-0-691-09565-3
• Evans, Lawrence C. (1998), Partial differential equations, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0772-9
• Folland, Gerald B. (1992), Fourier Analysis and Its Applications, Brooks-Cole, ISBN 978-0-534-17094-3
• Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets, Texts in Applied Mathematics, New York: Springer-Verlag, ISBN 978-0-387-98485-8
• Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (第2版), Harlow, Essex, England: Prentice-Hall (2002出版), ISBN 978-0-201-59619-9
• Krantz, Steven G. (1999), A Panorama of Harmonic Analysis, Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 978-0-88385-031-2
• Kreyszig, Erwin (1988), Advanced Engineering Mathematics (第6版), New York: John Wiley & Sons, ISBN 978-0-471-85824-9
• Kreyszig, Erwin (1989), Introductory functional analysis with applications, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-50459-7, MR 0992618
• Lang, Serge (1983), Real analysis, Addison-Wesley, ISBN 978-0-201-14179-5
• Lang, Serge (1993), Real and functional analysis, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94001-4
• Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, Toronto-New York–London: D. Van Nostrand Company, Inc., pp. x+190, hdl:2027/uc1.b4250788
• Template:Narici Beckenstein Topological Vector Spaces
• Template:Schaefer Wolff Topological Vector Spaces
• Treves, François (1967), Topological vector spaces, distributions and kernels, Boston, MA: Academic Press

歷史

• Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (PDF), Fundamenta Mathematicae (法文), 3: 133–181, doi:10.4064/fm-3-1-133-181, ISSN 0016-2736
• Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (德文)
• Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (法文), Paris: Hermann
• Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica, 22 (3): 227–261, doi:10.1006/hmat.1995.1024, MR 1347828
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (法文), Chez Firmin Didot, père et fils
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (德文), O. Wigand, reprint: Grassmann, Hermann (2000), Kannenberg, L.C. (編), Extension Theory, Kannenberg, Lloyd C.翻譯, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
• Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
• Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (德文), 原著喺2006-11-23歸檔
• Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025
• Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (義大利文), Turin
• Peano, G. (1901) Formulario mathematico: vct axioms via Internet Archive

更多

• Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics, Toronto: Thomson Learning, ISBN 978-0-03-083993-1
• Atiyah, Michael Francis (1989), K-theory, Advanced Book Classics (第2版), Addison-Wesley, ISBN 978-0-201-09394-0, MR 1043170
• Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64243-5
• Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64241-1
• Coxeter, Harold Scott MacDonald (1987), Projective Geometry (第2版), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96532-1
• Eisenberg, Murray; Guy, Robert (1979), "A proof of the hairy ball theorem", The American Mathematical Monthly, 86 (7): 572–574, doi:10.2307/2320587, JSTOR 2320587
• Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics,第150卷, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94269-8, MR 1322960
• Goldrei, Derek (1996), Classic Set Theory: A guided independent study (第1版), London: Chapman and Hall, ISBN 978-0-412-60610-6
• Griffiths, David J. (1995), Introduction to Quantum Mechanics, Upper Saddle River, NJ: Prentice Hall, ISBN 978-0-13-124405-4
• Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90093-3
• Halpern, James D. (Jun 1966), "Bases in Vector Spaces and the Axiom of Choice", Proceedings of the American Mathematical Society, 17 (3): 670–673, doi:10.2307/2035388, JSTOR 2035388
• Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013), Calculus : Single and Multivariable (第6版), John Wiley & Sons, ISBN 978-0470-88861-2
• Husemoller, Dale (1994), Fibre Bundles (第3版), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94087-8
• Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (第4版), Berlin, New York: Springer-Verlag, ISBN 978-3-540-25907-7
• Kreyszig, Erwin (1991), Differential geometry, New York: Dover Publications, pp. xiv+352, ISBN 978-0-486-66721-8
• Kreyszig, Erwin (1999), Advanced Engineering Mathematics (第8版), New York: John Wiley & Sons, ISBN 978-0-471-15496-9
• Luenberger, David (1997), Optimization by vector space methods, New York: John Wiley & Sons, ISBN 978-0-471-18117-0
• Mac Lane, Saunders (1998), Categories for the Working Mathematician (第2版), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2
• Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0
• Naber, Gregory L. (2003), The geometry of Minkowski spacetime, New York: Dover Publications, ISBN 978-0-486-43235-9, MR 2044239
• Schönhage, A.; Strassen, Volker (1971), "Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)", Computing (德文), 7 (3–4): 281–292, doi:10.1007/bf02242355, ISSN 0010-485X, S2CID 9738629
• Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish
• Stewart, Ian (1975), Galois Theory, Chapman and Hall Mathematics Series, London: Chapman and Hall, ISBN 978-0-412-10800-6
• Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, Prentice Hall, ISBN 978-0-13-535732-3
• Wallace, G.K. (Feb 1992), "The JPEG still picture compression standard" (PDF), IEEE Transactions on Consumer Electronics, 38 (1): xviii–xxxiv, CiteSeerX 10.1.1.318.4292, doi:10.1109/30.125072, ISSN 0098-3063, 原著 (PDF)喺2007-01-13歸檔, 喺2017-10-25搵到
• Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics.第38卷. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.