電腦模擬
電腦模擬(粵拼:din6 nou5 mou4 ji5;英文:computer simulation),又叫電腦仿真,係科學上嘅一種研究方法。研究者會整個數學模型出嚟模擬想研究嘅現象,個模型會講明個現象涉及邊啲變數同埋呢啲變數之間嘅方程式係點,跟住個研究者就會將個模型寫成電腦程式嚟行,睇吓「如果個數學模型正確,會發生乜嘢事」,做到按理論知識預測現實世界嘅現象。除此之外,電腦模擬通常會配合埋科學視覺化技術,將模擬結果以圖像形式呈現出嚟[1][2]。
舉個簡單例子說明,群動係電腦模擬嘅一個出名例子,想像家陣有一大柞個體一齊移動,途中佢哋會守三條規則:分隔-唔好撞到隔離嘅其他個體;順向-將自己方向對準周圍其他個體嘅平均;凝聚-將自己置於周圍其他個體嘅平均嘅位置。用電腦模擬嘅話,個程式會類似噉:
設 件物件; 設呢 件物件嘅初始位置 設 (時間)= 0; While 未到某個值, Foreach 物件 計「如果呢件物件跟嗰三條法則郁,佢嘅新位置會响邊」; 顯示出每件物件嘅新位置; 上升 1;
於是研究者就能夠知道「如果群動嘅數學模型正確,會發生乜嘢事(啲物件郁起上嚟望落會係點嘅樣)」。事實表明咗,群動模型可以準確噉預測某啲自然現象,例如係一大群雀鳥一齊飛嗰陣成個雀群成嘅形態[3]。
電腦模擬係科學運算不可或缺嘅一部份,喺物理學[4]、化學[5]同生物學[6]等嘅自然科學上都會用到。除此之外,電腦模擬仲有俾人用落去社會科學上,例如用博弈論模擬社會(想像「如果社會當中有咁多咁多百分比嘅人跟噉樣噉樣嘅法則做決策,個經濟體會變成噉樣噉樣」)[7],而工程學都有用到電腦模擬,例如模擬「如果部機械用噉嘅設計,部機械嘅效率會係咁高咁高」[8]。
以下嘅內容,假設讀者已經有齊嗮基本嘅程式編寫知識。
哲學背景[編輯]

係兩件嘢之間嘅引力嘅數值;
係第一件嘢嘅質量;單位係公斤(kg)
係第二件嘢嘅質量;單位係公斤(kg)
係兩件嘢之間嘅距離;單位係米(m)
所以要用腦諗「如果 、 同 係咁多咁多, 會係幾多」並唔難。但唔係個個科學理論都咁簡單。
電腦模擬係廿一世紀初嘅一種科研方法。科學係用科學方法[e 1]嚟追求知識,而科學方法涉及以下嘅步驟[10]:
- 根據手上已知係真嘅事實,諗一啲理論出嚟(「基於我哋經已觀察到嘅呢啲現象,我推測啲現象背後嘅法則係噉噉噉,令呢種現象出現」),而為求精確,呢啲理論通常都想係用數學模型嘅方式表達嘅;
- 跟手就靠邏輯嘅思考,去諗吓呢柞理論會做點樣嘅預測(「如果我提倡嘅呢個理論係真確嘅,理應會...」);
- 然後就做實驗同觀察嚟攞數據,驗證吓個理論嘅預測係咪真確(「如果我呢個理論係真確,呢個實驗理應會得出某個某個結果,而個實際嘅實驗結果係...」);
- 如果數據顯示,個理論係做唔到準確嘅預測嘅話,就要一係根據攞到嘅數據睇吓個理論要點改先可以令佢做到準確啲嘅預測,一係就要諗新理論取代舊理論[11]。
用電腦模擬做科研想要做嘅就係幫手預測複雜系統嘅行為:原則上,「一個理論會作出乜嘢預測」呢一點可以由個研究者齋靠諗嚟做得到,例子可以睇吓好似基本牛頓力學入面嗰啲相對簡單嘅物理定律-呢啲定律吓吓都係一條式得嗰幾個變數,研究者可以輕易噉用人手計出「根據呢條定律,如果變數 嘅數值係咁多咁多,變數 嘅數值應該會係咁多咁多」。不過當研究緊嗰樣現象有返咁上下複雜嗰陣,「齋靠個研究者用腦諗」好多時就會難令人信服[12]:p. 6,例如係群動噉,好難說服人話「齋靠研究者用腦諗,就會準確計到群動三定律會出點嘅樣嘅移動」。於是研究者就將自己個理論(用數學模型嘅方式表示)編寫成一個電腦程式,然後再行呢個程式,睇吓個程式會引致乜嘢結果-呢啲結果就會係佢個理論會作出嘅預測[13][14]。
電腦模擬係喺廿世紀嗰陣同電腦一齊冒起嘅:科學研究呢家嘢喺中世紀經已有,當時要計數淨係有得用人手計,而好似萬有引力定律等相對簡單嘅科學理論(條式通常得嗰 3 到 4 個變數)要用人手計並唔難,但一研究好似係群動呢啲涉及閒閒地幾廿個個體隨時間分別噉變化嘅現象,用人手計就會好撈絞;不過廿世紀初出咗一樣好重要嘅發明-電腦,電腦係運算機械,即係能夠用快過人手好多嘅速度做大量嘅運算,所以電腦嘅出現令到人類能夠計一啲以前計唔到嘅數學模型,引起咗科學家用電腦模擬嚟做科研。到咗廿一世紀初,電腦模擬經已成為咗科研一個不可或缺嘅部份[15]。
基本程式[編輯]
喺最基本上,一個做電腦模擬嘅程式(或者最少係做動態模擬嘅程式)可以想像成以下噉嘅虛擬碼[2]:
初始化(講明個模型有乜變數,想像其中一個變數叫「」); 設 (時間)= 0; While 未到某個值, 按個理論嘅數學模型,計吓個現象跟住會變成點(); 係一個函數。 顯示出個現象變成咗點嘅樣; 上升 1;[註 2]
呢個過程會俾研究者視覺化噉睇到「如果嗰個數學模型成立,噉會見到啲乜嘢現象」呢一樣資訊[註 3][14]。除此之外,一個電腦模擬仲可以將模擬途中嘅數據記低,例如記住「變數 喺每個時間點嘅數值」(即係好似下面段碼噉),跟手再將呢啲數據畫成圖表,即係例如 Y 軸表示變數 嘅數值,X 軸表示時間,畫一條線出嚟[1]。
t=0: y = 0
t=1: y = 0
t=2: y = 10
t=3: y = 30
t=4: y = 60
t=5: y = 100
...

主要分類[編輯]
電腦模擬可以按多種準則分類,包括咗係[註 4]:
有冇隨機性[編輯]

隨機[e 2]定決定[e 3]-前者指有隨機喺入面嘅電腦模擬,例如個程式其中一行碼係 rand(1,10);(隨機噉產生一個數值响 1 同 10 之間嘅數值),將模擬緊嗰個現象想像成有隨機喺入面,而後者就指冇呢啲隨機嘅電腦模擬[16]。
蒙地卡羅方法[e 4]係一種出名嘅隨機模擬做法。蒙地卡羅方法係用隨機嘅做法應付決定性系統嘅演算法,源於 1940 年代:如果話一個系統係「決定咗」嘅,意思係指個系統冇隨機喺裏面[17]。蒙地卡羅方法最基本嘅流程如下[18][19]:
- 定義個系統嘅輸入嘅可能數值(定義域[e 5]);
- 用一個表示輸入數值、受定義域限制嘅概率分佈[e 6]隨機噉產生一個輸入;
- 對個輸入做決定性嘅運算;
- 將步驟 2 同 3 重複 咁多次,得到 個輸出,再結合數據[e 7]-例如計嗰 個輸出嘅平均值。
舉個簡單例子說明,蒙地卡羅方法可以用嚟估計圓周率()嘅數值(睇附圖)[18]:
- 畫一個正方形,再喺個正方形入面畫個 90° 嘅扇形,任何嘅輸入坐標 都實會喺個正方形裏面(定義域);
- 用一個均勻分佈[e 8]產生一個輸入坐標數值,「均勻分佈」意思係指每個坐標可能數值出現嘅機會率都完全一樣;
- 喺產生咗出嚟輸入坐標數值嘅位置嗰度畫一點(做運算);
- 將步驟 2 同 3 重複 咁多次,然後數吓有幾多點點係喺個扇形裏面(同原點距離細過 1)嘅,設呢個數值做 ,如果 嘅數值大到接近無限大嘅話,以下呢樣嘢會成立:
好似蒙地卡羅方法噉嘅隨機模擬帶出咗個諗頭:無論個系統係咪決定性嘅都好,用帶有隨機嘅方法都有可能俾得到有返咁上下準嘅答案-「有返咁上下準」意思係指,得出嘅答案同真實嘅答案差距唔係咁大,未至於大到能夠對解決問題嘅效率造成明顯嘅負面影響。而事實表明咗,就算一個系統事實上冇隨機,好似蒙地卡羅方法噉嘅隨機模擬好多時都好使好用,例子可以睇吓蒙地卡羅樹搜尋相關嘅嘢[20][21]。
方程定個體[編輯]
電腦模擬仲可以分做方程為本[e 9]同個體為本[e 10]兩大種:方程為本模型常用於物理學同化學等嘅物理科學,指成個模型靠住一大柞嘅方程式-好多時會係微分方程-嚟表達啲變數之間嘅啦掕,呢啲方程式當中通常會係涉及時間(),所以隨住時間演進( 數值由 0 開始上升),個模型會係噉計算個系統嘅各變數响時間點每一刻數值會係幾多。例如以下呢段用 C 程式語言寫嘅源碼可以攞嚟模擬喺牛頓第二定律之下郁動嘅物體[22][註 5]:
double t = 0.0;
float dt = 1.0f;
float velocity = 0.0f;
float position = 0.0f;
float force = 10.0f;
float mass = 1.0f;
// 設一大柞變數,包括咗時間點(t)、時間間隔(dt)、速度(velocity)、位置(position)、件物體受嘅力(force)、同件物體嘅質量(mass)。
while ( t <= 10.0 ) // 重複噉計若干次,計到時間點係 10 為止。
{
position = position + velocity * dt;
velocity = velocity + ( force / mass ) * dt; // 用牛頓第二定律計吓件物體受嘅力同佢嘅質量會點影響佢嘅速度。
t += dt;
}
相比之下,個體為本模型涉及模擬一大柞嘅個體-個體為本模型比較常用於生物學同社會科學,因為呢啲領域研究嘅現象往往都涉及一大柞個體(人或者第啲生物)喺度個別噉做決策[23]。基本上,行個體為本模型嘅程式做嘅嘢可以用以下呢幾個步驟總括[24][25]:
- 初始化,建構 個(離散嘅)個體( 通常閒閒地係幾百),每一個個體都掕住一啲數值表示佢嘅個體特性[註 6](睇物件導向編程);
- 設做 0;
- 喺呢個時間點 ,foreach 個體,按呢個個體嘅行動法則同埋特性,計佢跟住落嚟嘅狀態會點變;
- 如果個模型涉及一啲整體嘅變數,按啲個體嘅新狀態嚟計呢啲整體變數嘅新數值;
t = t + 1( 數值上升 1);- 一路係噉重複步驟 3 至 5,直至結束條件達到為止。
上面提咗嘅群動就係個體為本模型嘅例子。

第啲分類[編輯]
除咗以上嘅分類法之外,電腦模擬仲可以按以下呢啲特性嚟分:
- 離散事件模擬[e 11]:指將模擬緊嗰個系統想像成喺離散時間()當中存在嘅一連串事件;每件事件都會喺某個時間點發生,並且引起個系統嘅狀態 變化(某啲變數嘅數值變),而且呢啲模型通常都假設咗個系統喺事件之間嘅時間內唔會起乜嘢變化[註 7]。大自然當中嘅系統好少可會話「冇事件發生就企喺度唔郁」,不過離散事件模擬喺工程學同商學就頗為常用-呢啲領域成日都會分析一啲人造嘅系統,例如係用離散事件模擬一間銀行嘅變化,當中會影響間銀行嘅狀態嘅事件包括「客人 出現」同「客人 出現」呀噉[26]。
- 多重規模模型[e 12]:指個模型會同時模擬多過一個層面嘅現象;如果話一個模型有「多層」,即係例如每層都會有一柞變數,而每層嘅變數都會係由下層嗰啲變數結合而成,
... 等等。
各領域嘅應用[編輯]
物理學[編輯]
1 冇任何物理法則。
2 有重力,但冇碰撞探測。
3 有重力同碰撞探測,但冇剛體動力學。
4 基本嘢冚唪唥齊嗮,最能夠創造迫真嘅郁動。
運算物理學涉及用運算方法(包括電腦模擬)解決物理學上撞到嘅問題:物理學通常都會用一大柞方程式(尤其係微分方程)表達某啲變數之間嘅關係,用呢啲變數組成嘅模型嚟描述研究緊嘅現象。做物理學相關工作嘅人成日都會用電腦模擬嚟處理一啲解析解(簡單講即係齋靠操弄方程式)搞唔掂嘅問題-呢啲問題往往係要做「想像 ,個答案係噉噉噉,想像 ,個答案係噉噉噉...」噉嘅運算方法嚟解(睇埋數值分析),而當個冇得用解析解嚟解嘅問題涉及複雜系統嗰陣,變數嘅數量多得好交關,難以靠人手計嚟解決個問題,於是研究者就會用電腦模擬嘅方法,叫部電腦(例如)「計 嗰陣嘅答案,計 嗰陣嘅答案... 再將呢啲答案畫一條線出嚟睇」[註 8][28]。
除此之外,用電腦嚟模擬物理現象仲可以幫到手製作更加迫真嘅虛擬世界-形成咗所謂嘅物理引擎[e 13]技術,呢種技術對電子遊戲同虛擬實境等嘅產品嚟講不可或缺[29]。例如類似以下呢段 C 碼噉嘅碼可以攞嚟模擬喺牛頓力學[e 14]二維空間下郁動嘅粒子[註 9][30],可以喺電子遊戲入面用嚟模擬物體嘅郁動:
...
while (currentTime < totalSimulationTime) { // 當 currentTime < totalSimulationTime,一路做...
for (int i = 0; i < NUM_PARTICLES; ++i) { // 家陣模擬若干粒粒子,foreach 粒子,做...
Particle *particle = &particles[i];
Vector2 force = ComputeForce(particle); // 有個子程序計吓呢粒粒子受緊幾多力。
Vector2 acceleration = (Vector2){force.x / particle->mass, force.y / particle->mass};
// 上面呢行碼係用牛頓第二定律計粒粒子跟住嘅加速度。
particle->velocity.x += acceleration.x * dt; // 用加速度 update X 軸速度...
particle->velocity.y += acceleration.y * dt; // 用加速度 update Y 軸速度...
particle->position.x += particle->velocity.x * dt; // 用速度 update X 軸位置...
particle->position.y += particle->velocity.y * dt; // 用速度 update Y 軸位置...
}
PrintParticles(); // 按啲粒子嘅位置,更新個畫面嘅樣。
currentTime += dt; // currentTime 上升 1。
}
...
生物學[編輯]

運算生物學涉及用運算方法(包括電腦模擬)解決生物學上撞到嘅問題:同(例如)運算物理學比起嚟,運算生物學比較傾向用個體為本模型,例如係進化論同生態學等領域上嘅研究都成日要分析一大柞個別噉做決策嘅個體(動物或者植物個體呀噉)之間嘅互動,以及係呢啲互動出嘅結果,而由於基因突變等嘅現象,生命呢家嘢本質上就實會有可能存在個體差異-因為噉,個體為本模型就啱嗮,例子可以睇吓對物競天擇等嘅現象嘅模擬[31][32]。
雖然話生命現象傾向似個體為本模型,但運算生物學當中都有用到方程為本模型,例如洛卡-伏塔拉模型[e 15]就係一個好出名嘅生物學方程為本模型,初頭呢個模型係俾人攞嚟模擬捕食者同獵物响生態系統當中嘅互動,打後呢個模型仲有俾人攞嚟模擬第啲生命現象。呢個模型涉及咗以下呢兩條非線性微分方程[33]:
當中
- 係獵物(例:兔仔)嘅個體數量;
- 係捕食者(例:狼)嘅個體數量;
- 表示時間;
- 表示獵物個體數量隨時間嘅導數,即係獵物個體數量嘅瞬間變率(詳情可以睇微積分);
- -呢個數值取決於 (獵物嘅數量會影響跟住落嚟有幾多隻新嘅獵物出世)同 (獵物同捕食者嘅數量會共同影響跟住落嚟有幾多隻獵物死亡)。
- 表示捕食者個體數量隨時間嘅導數;
- -呢個數值取決於 (捕食者嘅數量會影響跟住落嚟有幾多隻新嘅捕食者出世)同 (獵物同捕食者嘅數量會共同影響跟住落嚟有幾多隻捕食者因為捉唔到獵物而餓死)。
- 、、、 係一柞實數參數,反映獵物同捕食者「平均每隻生產幾多隻後代」等嘅因素;
如果將 同 畫做圖(打橫嗰條軸係時間[註 10]),會出好似以下呢兩條噉嘅線(藍線表示捕食者;紅線表示獵物):

跟住研究者仲有得調整吓啲參數,睇睇(例如)捕食者出生率突然勁跌會點樣影響個生態系統嘅情況[33]。
認知科學[編輯]
認知科學上都有用到電腦模擬-電腦模擬可以攞嚟研究認知(運算認知)同神經系統(運算神經科學),而人工智能(AI)本質上就係嘗試緊用電腦方法嚟模擬智能,務求教電腦展現出好似有智能噉嘅行為[34][35]。例如人工神經網絡[e 16]就係一種好出名嘅認知科學模型[36]。人工神經網絡個諗頭係要用人工方法模仿動物神經細胞嘅功能:一粒動物神經細胞喺受到某啲特定刺激嗰陣,會用電或者化學方式向第啲神經細胞傳出訊號,然後同呢粒神經細胞相連嗰啲神經細胞會受到佢嘅訊號刺激,跟住又會各自噉射新嘅訊號-於是資訊就會喺成個神經系統當中傳播開去[37];一個人工神經網絡由大量嘅人工神經細胞組成,喺用電腦程式整神經網絡嗰陣,研究者會每粒人工神經細胞都同佢設個數值代表佢嘅啟動程度[e 17][38],而每粒神經細胞嘅啟動程度嘅數值都有條式計,呢條式包括咗喺佢之前嗰啲神經細胞嘅啟動程度[39]。即係例如個程式 foreach 細胞有一條類似噉樣嘅算式:
- ;(啟動函數)
代表粒神經細胞嘅啟動程度, 代表前嗰排嘅神經細胞當中第 粒嘅啟動程度,而 就係前嗰排嘅神經細胞當中第 粒嘅權重(指嗰粒細胞有幾影響到 )。所以當一粒人工神經細胞啟動嗰陣,會帶起佢後面啲細胞跟住佢啟動-似十足生物神經網絡入面嗰啲細胞噉。假如個神經網絡嘅程式令佢能夠自行按照經驗改變 嘅數值嘅話,佢就會曉學習[40]。

到咗廿一世紀初,人工神經網絡經已俾科學界廣泛噉用落去各種各樣嘅問題嗰度。喺應用上,事實證實咗人工神經網絡能夠處理機械視覺同埋語音識別呢啲傳統嘅電腦程式好難解決到嘅問題[42][43];而喺理論性質嘅認知科學上亦有聯結主義[e 18]理論,主張心靈可以用人工神經網絡嚟模擬[44],例如有研究就成功噉用人工神經網絡令人工智能好似人噉識得睇一幅圖決定要將注意力擺喺幅圖嘅邊一忽[45]。
社會科學[編輯]
運算社會科學係指用運算方法研究社會科學,例如用電腦模擬解析社會現象。有學者指,電腦模擬呢種技術助長廿世紀起經濟學等嘅領域放棄唔真實嘅假設:廿世紀前嘅古典經濟學成日會做一啲唔真實嘅假設,包括假設咗啲經濟個體喺做經濟決策嗰陣係乜都知嘅(例如假設每個買家知道嗮市場裏面啲貨嘅價格),呢個假設好明顯唔合符現實[46],但當時嗰啲研究者受到運算能力嘅局限-要計「如果每個個體响資訊上都有差異,個模型會得出乜結果」需要做嘅運算量大得滯,用人手根本做唔嚟(例:想像個模型模擬 1,000 個個體,佢哋個個性格都唔同,研究者要人手噉逐個逐個計佢哋嘅決策結果);呢點搞到啲學者明知個假設唔真實,都焗住要照用。廿世紀電腦模擬技術有咗好似個體為本模型噉嘅架生,令到經濟學家喺建立佢哋嘅模型嗰時可以考慮埋個體差異,助長咗經濟學上嘅革新[47]。
博弈論[e 19]上嘅研究成日都會用到個體為本模型,當中重複監犯困境[e 20]就係一個出名嘅例子:監犯困境係一種博弈;喺一場監犯困境當中,每位博弈者有兩個選擇-合作同背叛;而一場兩人監犯困境嘅報償矩陣如下,每個格嗰兩個數值表示兩個人嘅分別所得[48]:
| 紅色揀合作 | 紅色揀背叛 | |
|---|---|---|
| 藍色揀合作 | ||
| 藍色揀背叛 |
定義上,喺監犯困境當中,以下呢條不等式成立(假設報償值係愈正愈理想):
例:;簡單講,監犯困境係指大家合作就可以得到 咁多利益,一位博弈者單方面背叛可以攞到著數(),但如果雙方都背叛就大家齊齊輸()[48]。重複監犯困境係指啲博弈者進入監犯困境嘅情境若干次[49][50]。
有研究者進行電腦模擬研究,行個體為本模型模擬重複監犯困境,喺最簡單嘅情況下即係[51]:
- 初始化,將
R、T、S同P設定做特定嘅數值; - 建立 個模擬嘅個體,每個個體有兩個屬性-「採取嘅策略」
strat同埋「累積咗嘅總得益」jik; - 是但抽兩個個體,俾佢哋進行監犯困境博弈,每位模擬嘅博弈者會按佢嘅
strat做決策; - 按每個個體做嘅決定,計佢嘅總得益點變,例如兩個都揀咗合作嘅話,噉佢哋每個人都
jik = jik + R; - 重複步驟 3 同 4 若干次;
原則上,「最成功嘅策略」係指令到個體嘅總得益最大化嘅策略,所以研究者要做嘅嘢係喺步驟 3 同 4 重複咗若干次之後,foreach 策略類型,(例如)計吓採取嗰種策略嘅個體嘅平均 jik,而呢個數值最高嗰種策略就係「最成功嘅策略」。結果發現,「永遠淨係揀合作」係一種非常惡劣嘅策略,會搞到個個體係噉勁俾人背叛而最後輸(假設 ,而且 數值有咁上下大)。啲研究者就靠呢個結果作出推論:重複監犯困境就好似人嘅現實生活噉-人係一種有社會性嘅動物,往往會一齊合作先可以做到最多嘢(),但喺合作嘅情境當中,成日都會出現機會容許某啲參與者搵第啲參與者老襯(背叛係有可能發生嘅,而且 ),而世界唔係烏托邦,完全利他嘅人係缺乏靠自己生存嘅能力嘅-人實要識得喺俾人背叛嗰陣,用返背叛嚟應對,以防俾人搵老襯[52]。
工程學[編輯]
運算工程學涉及用電腦模擬等嘅運算方法分析工程學上應付嘅人造系統(例如機械同建築物)。喺運算工程學上,電腦模擬通常會以物理學知識做基礎[註 11],即係「分析緊個系統,個系統嘅原理涉及咗呢柞呢柞物理定律,將個系統涉及嗰啲物理定律編寫做程式,再行嚟睇,就做到模擬個系統行起上嚟會係點」[53]。
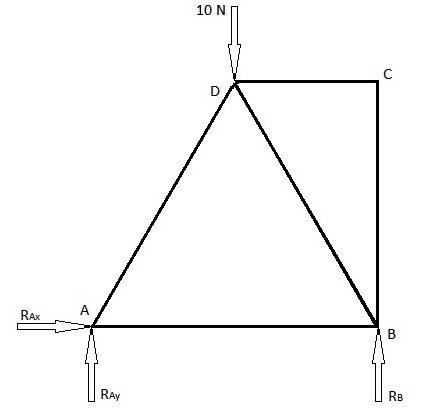
例如廿一世紀初嘅結構分析[e 21]就時不時都會用到電腦模擬:結構分析常用於土木工程-包括咗結構工程同建築工程-指個工程師分析一個結構同埋嗰個結構嘅各橛分別受到點樣嘅負荷,以及係分析呢啲負荷會對個結構造成乜嘢影響(例如係會唔會砸冧個結構),對於建設安全嘅結構嚟講不可或缺[54],例如想像以下呢個噉嘅簡單結構,個結構係個等邊三角形,個工程師打算用呢個結構嚟撐住啲嘢,個結構要承受一股由上面壓落嚟嘅力,股力嘅大細係 咁多:
由力學上嘅知識(作為分析基礎嘅物理學知識)已知,呢股力會造成一股反作用力。而假設組成個結構嗰啲樑夠嗮硬淨唔會變形(剛體),而且啲節點又夠勁(啲樑唔會走位),噉啲反作用力(、、)會係噉嘅樣(想像啲節點有特殊構造):
而按物理學上對力嘅知識,如果成個結構企到喺度唔郁(個結構會郁就表示可能會冧),噉啲力加埋嗮係 0,即係話喺 嗰點嘅力可以噉樣想像( 係沿打戙嗰條軸嘅力, 係沿打橫嗰條軸嘅力,因為個結構係等邊三角形,所以每隻角嘅角度係 60°):
... 喺另外嗰幾點嘅力可以用同樣嘅道理嚟諗。如是者,個工程師就計到嗮「每條樑會受幾多力」等嘅重要資訊。上述呢個係一個簡化嘅例子:喺現實應用上,大些少嘅建築物會有成千上萬個類似噉嘅結構部件,唔可能人手計嗮。所以廿世紀末以來嘅工程師都會搵電腦模擬幫手,將結構唔同部份之間嘅互動定律組裝成矩陣,然後解方程,得出結構每部分需要受幾多力同會郁幾多,知道成棟嘢會唔會因為噉而有機會冧,俾工程師做「成棟建築物噉樣起得唔得」嘅判斷[54]。
複雜啲嘅工程運算會涉及唔係線性嘅自然定律,呢啲定律加埋日常物件形狀上嘅不規則,工程運算原則上冇絕對準嘅答案,只能夠將現實處境拆做好多嚿細細個、會彼此互動嘅組件,然後用電腦模擬計個大約啱嘅答案出嚟。呢種做法就叫做有限元分析[55]。
驗證同確認[編輯]
喺做咗一場電腦模擬之後,研究者仲要評估個模型掂唔掂:電腦模擬用嘅模型梗會涉及抽象化,即係有一啲特徵係現實嗰樣現象有、但個模型係冇嘅;例如工程學上用電腦模型模擬機械或者建築物等嘅結構嗰時,就好興假設組成個結構嗰啲柱同樑係剛體唔會變形-原則上,呢個假設係一種理想化,現實世界冇任何嘢係真正嘅剛體,不過如果啲建築材料真係造得好精良,硬淨得好交關,硬淨到要極大嘅力(例如有嚿隕石撞落去)先可以搞到佢變形,而呢啲「極大嘅力」出現嘅機率微乎其微(「有嚿隕石跌落嚟」係一件好少可會發生嘅事件)[56],噉「個結構係剛體」呢一點喺絕大多數時候都會成立,所以個假設雖然唔真實,但唔會對分析嘅準確度造成顯著嘅負面影響,可以照用[57]。由呢個例子睇得出,一個電腦模擬模型實會有可能做唔到準確噉描述現實,問題只係「個模型失敗嘅機率有幾大」(一般係愈低愈好)同「個模型會喺幾多個情況下啱用」(一般係愈多愈好)。
評估一個電腦模擬模型主要有兩大過程-驗證[e 22]同確認[e 23][58][59]:
- 驗證係指睇吓個模型嘅輸出同原模型嗰啲微分方程嘅解答接唔接近;呢個過程包括檢查個模型啲源碼做嘅運算係咪同預想中嘅演算法相同,仲有係睇吓用個模型計出嚟嘅結果係咪合符用解析解得出嘅結果(如果個模型模擬嗰樣現象係有可能用解析解計嘅話)[註 12]。
- 確認係指睇吓個模型「表示到現實嗰樣系統嘅程度」係咪足以達到場電腦模擬嘅目的;呢個過程通常會涉及個研究者行完場模擬之後走去做實驗攞數據,睇吓啲數據係咪真係合乎個模型嘅預測,例如一個工程師做電腦模擬,模擬一個新設計嘅摩打行起上嚟係點,個模型預測個摩打嘅效率「會係咁多咁多」,而個模型預測嘅效率數值非常好(根據佢個理論,個摩打效率非常咁高),令佢有信心郁手整個摩打嘅原型出嚟;响整好咗個原型之後,佢就開始試行吓個原型摩打,並且搵方法量度個摩打嘅效率(攞到數據)-「啲數據係咪合符佢嘅原先預期」就反映佢個模型掂唔掂。
創發嘅啟示[編輯]
有哲學家指出,電腦模擬對理解創發[e 24]嘅現象嚟講至關重要[61]。創發係一種現象,指一樣由好多唔同部份組成嘅事物具有一啲佢組成部份冇嘅特性。好似係水噉,水喺化學上由氫同氧呢兩種化學元素組成嘅,水喺正常溫度同壓力下處於液體狀態,而呢種特性係氫同氧都冇嘅(氫同氧喺正常溫度壓力下會呈氣體狀態)-水具有最少一樣「氫同氧唔具有嘅特性」(創發出嚟嗰樣特性);又或者好似係一個人噉,一個正常健康嘅人識行路識思考,而呢啲嘢都係組成人類身體嘅個別細胞唔能夠獨力做到嘅[62];創發仲可以分做兩種-弱創發同強創發,弱創發係指創發出嚟嗰樣特性係可以由啲組成部份嘅特性解釋嘅,而強創發係指創發出嚟嗰樣特性係冇得由啲組成部份嘅特性嚟解釋[註 14][63]。
呢啲哲學家主張,電腦模擬嘅技術好幫到手理解弱創發嘅現象:研究者可以將一個預想中嘅系統寫做一個電腦模擬程式,個程式曉做(人手計唔嚟嘅)「foreach 組成部份,做噉噉噉嘅運算」;而事實係,會用得電腦模擬嘅,好多時都係因為研究緊嗰樣現象有返咁上下複雜,齋靠用個人腦諗唔能夠想像到個系統會出現乜嘢特性;不過假設個模型係掂嘅,個研究者跟住就有得靠住個模型,睇到個整體系統會出現啲乜嘢特性-包括係個系統有冇啲柞組成部份冇嘅特性,從而攞到一啲冇電腦模擬就攞唔到、有關弱創發嘅資訊[64]。
註釋[編輯]
- ↑ 係一個常數,數值係 6.674×10−11 N • (m/kg)2。
- ↑ 喺某啲電腦模擬當中,逐步升嘅唔係時間 ,而係第個變數。
- ↑ 技術化啲講,電腦模擬嘅過程會涉及離散化-假想時間係連續嘅,好似上述噉嘅電腦模擬實會將 想像成一個離散變數。
- ↑ 以下呢啲類型有好多都唔係互斥嘅,一個電腦模擬程式有可能同時屬於多過一個類別。例如隨機同決定之間定義上就係互斥嘅,但隨機同個體為本呢兩個類別唔互斥。
- ↑ 呢個模型冇隨機,所以屬決定性模型。
- ↑ 呢點令佢哋同物理學上研究嘅粒子唔同-同一個種類嘅粒子粒粒都一個板,但同一個物種嘅唔同個體可以有唔同性格。
- ↑ 即係話設 表示「時間點 嘅 」,如果 同 之間冇事件發生,噉 。
- ↑ 會輸出一個列表,列嗮啲數值出嚟。
- ↑ 初始化嗰部份省略咗。
- ↑ 會涉及「foreach 時間點」噉嘅運算,用人手計會好撈絞。
- ↑ 不過工程學都有分好多門,例如化學工程就會用多啲化學知識。
- ↑ 有人因此而批評,話「驗證」嘅概念根本冇用-研究者想用電腦模擬通常就正正係因為個問題用解析解搞唔掂。
- ↑ 再配合埋實驗攞到嘅數據。
- ↑ 不過都有學者覺得呢種分法係多餘。
睇埋[編輯]
文獻[編輯]
- Desa, W. L. H. M., Kamaruddin, S., & Nawawi, M. K. M. (2012). Modeling of aircraft composite parts using simulation (PDF). In Advanced Materials Research (Vol. 591, pp. 557-560). Trans Tech Publications Ltd.
- Hartmann, S. (1996). The world as a process (PDF). In Modelling and simulation in the social sciences from the philosophy of science point of view (pp. 77-100). Springer, Dordrecht.
- Humphreys, P. (2004). Extending ourselves: Computational science, empiricism, and scientific method. Oxford University Press.
- Kaizer, J. S., Heller, A. K., & Oberkampf, W. L. (2015). Scientific computer simulation review (PDF). Reliability Engineering & System Safety, 138, 210-218.
- Macal, C. M., & North, M. J. (2008, December). Agent-based modeling and simulation: ABMS examples (PDF). In 2008 Winter Simulation Conference (pp. 101-112). IEEE.
- McClelland, J. L. (2009). The place of modeling in cognitive science (PDF). Topics in Cognitive Science, 1(1), 11-38.
- Nutaro, J. J. (2011). Building software for simulation: Theory and algorithms, with application in C++ (PDF). John Wiley & Sons Ltd.
- Schelling, T. C., (1971). "Dynamic Models of Segregation (PDF)," Journal of Mathematical Sociology, 1: 143–186.
- Winsberg, E. (2003). Simulated experiments: Methodology for a virtual world (PDF). Philosophy of science, 70(1), 105-125.
引述[編輯]
- ↑ scientific method
- ↑ stochastic
- ↑ deterministic
- ↑ Monte Carlo method
- ↑ domain
- ↑ probability distribution
- ↑ aggregate data
- ↑ uniform distribution
- ↑ equation-based
- ↑ agent-based
- ↑ discrete event simulation,DES
- ↑ multiscale modeling
- ↑ physics engine
- ↑ Newtonian mechanics
- ↑ Lotka-Volterra model
- ↑ artificial neural network
- ↑ activation level
- ↑ connectionism
- ↑ game theory
- ↑ iterated prisoner's dilemma
- ↑ structural analysis
- ↑ verification
- ↑ validation
- ↑ emergence
- ↑ 1.0 1.1 Strogatz, Steven (2007). "The End of Insight". In Brockman, John (ed.). What is your dangerous idea?. HarperCollins.
- ↑ 2.0 2.1 Donald Craig (1996). The Simulation Algorithm.
- ↑ Reynolds, Craig W. (1987). "Flocks, herds and schools: A distributed behavioral model.". ACM SIGGRAPH Computer Graphics. 21. pp. 25–34.
- ↑ Thijssen, J. (2007). Computational physics. Cambridge university press.
- ↑ Lewars, E. (2003). Computational chemistry. Introduction to the theory and applications of molecular and quantum mechanics, 318.
- ↑ Banzhaf, W., & Eckman, F. H. (1995). Evolution and biocomputation: computational models of evolution (Vol. 899). Springer Science & Business Media.
- ↑ Macy, M. W., & Skvoretz, J. (1998). The evolution of trust and cooperation between strangers: A computational model. American Sociological Review, 638-660.
- ↑ Huff, G. H., Feng, J., Zhang, S., Cung, G., & Bernhard, J. T. (2004). Directional reconfigurable antennas on laptop computers: Simulation, measurement and evaluation of candidate integration positions. IEEE Transactions on Antennas and Propagation, 52(12), 3220-3227.
- ↑ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006". Reviews of Modern Physics. 80 (2): 633–730.
- ↑ Curd, M., & Cover, J. A. (1998). Philosophy of science: The central issues. C. Pincock (Ed.). New York: WW Norton.
- ↑ Godfrey-Smith 2003, Chapter 14: "Bayesianism and Modern Theories of Evidence".
- ↑ McClelland, J. L. (2009). The place of modeling in cognitive science (PDF). Topics in Cognitive Science, 1(1), 11-38.
- ↑ Winsberg, E. (2001). Simulations, models, and theories: Complex physical systems and their representations (PDF). Philosophy of Science, 68(S3), S442-S454.
- ↑ 14.0 14.1 Winsberg, E. (2003). Simulated experiments: Methodology for a virtual world (PDF). Philosophy of science, 70(1), 105-125.
- ↑ Bratley, Paul; Fox, Bennet L.; Schrage, Linus E. (2011-06-28). A Guide to Simulation. Springer Science & Business Media.
- ↑ Pinsky, M., & Karlin, S. (2010). An introduction to stochastic modeling. Academic press.
- ↑ Kroese, D. P.; Brereton, T.; Taimre, T.; Botev, Z. I. (2014). "Why the Monte Carlo method is so important today". WIREs Comput Stat. 6 (6): 386–392.
- ↑ 18.0 18.1 Kalos, Malvin H.; Whitlock, Paula A. (2008). Monte Carlo Methods. Wiley-VCH.
- ↑ Abramson, B. (2014). The expected-outcome model of two-player games. Morgan Kaufmann.
- ↑ Wolfgang Ertel; Johann Schumann; Christian Suttner (1989). "Learning Heuristics for a Theorem Prover using Back Propagation.". In J. Retti; K. Leidlmair (eds.). 5. Österreichische Artificial-Intelligence-Tagung. Informatik-Fachberichte 208,pp. 87-95. Springer.
- ↑ Suttner, C., & Ertel, W. (1990, July). Automatic acquisition of search guiding heuristics. In International Conference on Automated Deduction (pp. 470-484). Springer, Berlin, Heidelberg.
- ↑ Integration Basics: How to integrate the equations of motion 互聯網檔案館嘅歸檔,歸檔日期2018年10月26號,.. Gaffer on Games.
- ↑ Parker, W. S. (2008). Franklin, Holmes, and the epistemology of computer simulation 互聯網檔案館嘅歸檔,歸檔日期2021年6月9號,. (PDF). International Studies in the Philosophy of Science, 22(2), 165-183.
- ↑ Shoham, Yoav; Leyton-Brown, Kevin (2009). Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations. Cambridge University Press.
- ↑ Schelling, T. C., (1971). "Dynamic Models of Segregation 互聯網檔案館嘅歸檔,歸檔日期2021年6月5號,. (PDF)," Journal of Mathematical Sociology, 1: 143–186.
- ↑ Robinson, S. (2014). Simulation: the practice of model development and use. Palgrave Macmillan.
- ↑ Luo, X., & Qin, Y. (2018). Hybrid machining: theory, methods, and case studies. Academic Press.
- ↑ Numerical Solution of Differential Equations.
- ↑ Millington, I. (2007). Game physics engine development. CRC Press.
- ↑ Video Game Physics Tutorial - Part I: An Introduction to Rigid Body Dynamics. Developers.
- ↑ McLane, A. J., Semeniuk, C., McDermid, G. J., & Marceau, D. J. (2011). The role of agent-based models in wildlife ecology and management. Ecological Modelling, 222(8), 1544-1556.
- ↑ Vincenot, C. E., Giannino, F., Rietkerk, M., Moriya, K., & Mazzoleni, S. (2011). Theoretical considerations on the combined use of System Dynamics and individual-based modeling in ecology. Ecological Modelling, 222(1), 210-218.
- ↑ 33.0 33.1 Brauer, F., Castillo-Chavez, C., & Castillo-Chavez, C. (2012). Mathematical models in population biology and epidemiology (Vol. 2, p. 508). New York: Springer.
- ↑ Simon, H. (1991). Models of my life. New York: Basic Books.
- ↑ Rosenblatt, F. (1961). Principles of neurodynamics. Washington, D.C.: Spartan Books.
- ↑ "Artificial Neural Networks as Models of Neural Information Processing | Frontiers Research Topic". Retrieved 2018-02-20.
- ↑ Herz, A. V., Gollisch, T., Machens, C. K., & Jaeger, D. (2006). Modeling single-neuron dynamics and computations: a balance of detail and abstraction. Science, 314(5796), 80-85.
- ↑ The Machine Learning Dictionary - activation level 互聯網檔案館嘅歸檔,歸檔日期2018年8月26號,..
- ↑ Tahmasebi; Hezarkhani (2012). "A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation". Computers & Geosciences. 42: 18–27
- ↑ Ivakhnenko, A. G.; Grigorʹevich Lapa, Valentin (1967). Cybernetics and forecasting techniques. American Elsevier Pub. Co.
- ↑ "Artificial Neural Networks as Models of Neural Information Processing | Frontiers Research Topic". Retrieved 2018-02-20.
- ↑ Akira Hirose, Shotaro Yoshida (2012). "Generalization Characteristics of Complex-valued Feedforward Neural Networks in Relation to Signal Coherence". IEEE TNNLS, 23(4): 541-551.
- ↑ Forrest M.D. (April 2015). "Simulation of alcohol action upon a detailed Purkinje neuron model and a simpler surrogate model that runs >400 times faster". BMC Neuroscience. 16 (27): 27.
- ↑ Marcus, Gary F. (2001). The Algebraic Mind: Integrating Connectionism and Cognitive Science (Learning, Development, and Conceptual Change). Cambridge, Massachusetts: MIT Press. pp. 27–28.
- ↑ Peters, R. J., & Itti, L. (2007, June). Beyond bottom-up: Incorporating task-dependent influences into a computational model of spatial attention (PDF). In 2007 IEEE conference on computer vision and pattern recognition (pp. 1-8). IEEE.
- ↑ Rappaport, Steven (28 July 1996). "Abstraction and Unrealistic Assumptions in Economics". Journal of Economic Methodology. 3 (2): 215–236.
- ↑ Macal, C. M., & North, M. J. (2008, December). Agent-based modeling and simulation: ABMS examples (PDF). In 2008 Winter Simulation Conference (pp. 101-112). IEEE.
- ↑ 48.0 48.1 Poundstone, William (1993). Prisoner's Dilemma (1st Anchor Books ed.). New York: Anchor. pp. 8, 117.
- ↑ Beaufils, B., Delahaye, J. P., & Mathieu, P. (1997, July). Our meeting with gradual, a good strategy for the iterated prisoner's dilemma. In Proceedings of the Fifth International Workshop on the Synthesis and Simulation of Living Systems (pp. 202-209). MIT press.
- ↑ Wallace, H. M., Exline, J. J., & Baumeister, R. F. (2008). Interpersonal consequences of forgiveness: Does forgiveness deter or encourage repeat offenses?. Journal of Experimental Social Psychology, 44(2), 453-460.
- ↑ Shoham, Yoav; Leyton-Brown, Kevin (2009). Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations. Cambridge University Press.
- ↑ Axelrod's Tournament. Stanford Computer Science.
- ↑ Takizawa, K. (2014). Computational engineering analysis with the new-generation space-time methods. Computational Mechanics, 54(2), 193-211.
- ↑ 54.0 54.1 McKenzie, W. M. (2013). Examples in structural analysis (PDF). CRC Press.
- ↑ Potts, D. M.; Zdravković, L. (1999). Finite element analysis in geotechnical engineering. Thomas Telford. ISBN 9780727727534.
- ↑ Nester, C. J., Liu, A. M., Ward, E., Howard, D., Cocheba, J., & Derrick, T. (2010). Error in the description of foot kinematics due to violation of rigid body assumptions. Journal of biomechanics, 43(4), 666-672.
- ↑ Timan, A. F. (2014). Theory of approximation of functions of a real variable. Elsevier.
- ↑ Parker, W. (2013). Computer Simulation, in S. Psillos and M. Curd (eds.), The Routledge Companion to Philosophy of Science, 2nd Edition, London: Routledge.
- ↑ Oberkampf, W. and C. Roy, (2010). Verification and Validation in Scientific Computing, Cambridge: Cambridge University Press.
- ↑ Heckbert, S., Baynes, T., & Reeson, A. (2010). Agent‐based modeling in ecological economics 互聯網檔案館嘅歸檔,歸檔日期2021年12月6號,. (PDF). Annals of the New York Academy of Sciences, 1185(1), 39-53.
- ↑ Humphreys, P. (2004). Extending ourselves: Computational science, empiricism, and scientific method. Oxford University Press.
- ↑ O'Connor, Timothy; Wong, Hong Yu (February 28, 2012). Edward N. Zalta (ed.). "Emergent Properties". The Stanford Encyclopedia of Philosophy (Spring 2012 Edition).
- ↑ Bedau, Mark A. (1997), Weak Emergence (PDF).
- ↑ Bedau, M. A. (2013). Weak emergence and computer simulation. In Models, simulations, and representations (pp. 109-132). Routledge.