機械學習
機械學習(粵拼:gei1 haai6 hok6 zaap6;英文:ML)係人工智能一個子領域,專門研究點樣設計一啲特殊嘅演算法同統計模型,嚟去教電腦喺唔使個用家開口俾明文指示嘅情況下,學識有效噉樣做一啲特定嘅作業。機械學習嘅典型做法如下[2][3]:p. 2:
- 編寫一個電腦程式,教部電腦點樣由數據嗰度建立一個數學模型嚟描述佢對啲變數之間嘅關係嘅知識;
- 搵啲樣本數據(即係所謂嘅訓練數據)返嚟,俾個程式處理吓啲數據入面嘅個案,等部電腦按個程式建立一個數學模型;跟住
- 喺將來再撞到同類個案嗰時,部電腦就會曉按佢個程式,用建立咗嗰個模型,對呢啲之前未見過嘅個案作出預測-個設計者唔使明文噉教部電腦點樣應對呢啲前所未見嘅個案,部電腦都會有能力一定程度上應對。
機械學習演算法做嘅嘢係令部電腦曉「用手上資訊,自動噉預測某啲特定嘅變數嘅數值」,所以機械學習嘅技術可以將「做預測」呢家嘢自動化,而因為「做預測」呢家嘢喺好多領域都會用到,機械學習可以有好多實用價值,例如係[4]:
- 醫療:機械學習可以用嚟教電腦由手上嘅醫療數據,學識邊啲病徵同邊啲病症有關,所以可以攞嚟幫手診斷病人(用手上病人嘅病徵預測佢有乜嘢病)[5]。
- 金融:機械學習上有技術可以教電腦由手上嘅金融(例如係之前嗰幾個月嘅股價)嚟預測打後股價會點變化,呢點喺金融業上可以幫手做預測[6]。
- 市場學:機械學習可以用嚟教電腦由過去有關唔同產品嘅銷售量嘅數據,預測將來(間公司想出)嘅同類產品嘅銷售量[7]。
... 等等。
機械學習同數據科學好有關係,例如係做數據探勘噉,就可以涉及教部電腦點樣搵出數據當中嘅規律,令到部電腦曉自動化噉探勘一啲人手好難分析嘅數據,由呢啲數據嗰度抽取有用嘅資訊,而因為「由數據抽取資訊」呢樣嘢基本上無論乜嘢科學同商學領域都會用到,所以機械學習對於好多領域嚟講都係一種好有用嘅技術[8][9]。
概論
[編輯]定位
[編輯]| 「 | 」 |
上述呢個定義避免咗一啲歧義嘅問題:英國數學家亞倫圖靈[e 1]曾經對人工智能問「機械有冇能力思考?」呢條問題,所以有人提出將人工智能(包括機械學習)定義做研究點樣教機械思考嘅領域。但呢個定位俾好多科學家嫌佢含糊得滯(例如「思考」呢個詞應該要定義就經已好摎攪[11]),所以研究機械學習嘅科學家一般唔主張用呢個詞定義一個領域;而相比之下,上述嘅定義唔使依賴啲乜嘢零舍含糊嘅詞語-呢個定義只係要求電腦程式有類似人噉嘅行為,所以俾人覺得比較適合用嚟做成個科學領域嘅定位[11]。
理論基礎
[編輯]
一個學習者(無論係機械定係人)嘅主要目的係要將經驗普遍化[e 2][12]:由經歷過嘅嘢當中,抽取嗰啲嘢普遍具有嘅特性,並且用呢啲資訊嚟解難;例如一個人喺俾隻狗咬過之後,可能會產生狗普遍傾向會咬人嘅諗頭,並且從此之後傾向避開狗(將呢一隻狗會咬我普遍化成狗普遍都會咬我)。機械學習都係同一道理:做機械學習會俾一部電腦處理一啲數據,再要部電腦對於一啲佢之前未見過嘅同類個案作出預測,好似係一啲金融上會用嘅機械學習程式噉,設計者嘗試教部電腦用過去嘅股價數據預測將來嘅股價(將我處理過嗰啲股票嘅變化法則普遍化做股票股價變化普遍會跟嘅法則)[3][13]。
用統計學行話講嘅話,呢個過程如下:學習用嘅數據係出自一個有特定概率分佈[e 3]嘅現實,而假設柞數據係大致上準確噉代表到嗰個現實嘅概率分佈嘅(柞數據嘅概率分佈同個現實嘅近乎一樣),噉個機械學習程式就要靠佢嘅演算法加埋啲數據,砌返個合乎現實嘅數學模型出嚟[14]。
舉個例說明:想像家陣有個常態分佈([e 4]睇附圖),佢 X 軸表示研究緊嘅變數,而 Y 軸就反映咗變數每個值出現嘅機會率。如果 X 軸代表人類嘅身高,噉個常態分佈表達嘅嘢如下:人類嘅身高最常喺中間嗰個數值(嗰個數值出現率最高),而距離中間嗰個數值愈遠嘅身高值就出現得愈少(好少有極高或者極矮嘅人)。個常態分佈條線會有一條相應嘅方程式。而家假想個常態分佈代表住全人類嘅身高,跟住研究者抽一個樣本,例如係由全世界嘅人當中搵 500 個返嚟,量度佢哋嘅身高。喺最理想嘅情況之中,個樣本會完美噉代表到人類總體嘅身高分佈-即係話如果將個樣本入面嘅身高值同每個值出現嘅率畫條線,條線嘅形狀會同總體人類嗰條完全一個板。而如果家陣話要訓練一個機械學習程式,去靠個樣本嘅數據學習人類嘅身高分佈,個程式要做嘅嘢就係「由啲數據嗰度,砌返一個代表到人類總體身高分佈嗰條線嘅數學式出嚟」[3]。
運算學習論[e 5]係專門研究機械學習演算法嘅表現嘅電腦科學子領域。呢個領域會用到大量嘅統計學技巧分析機械學習所要面對嘅問題,例如係喺抽樣本嘅過程當中,一般都假設咗個樣本代表到所研究嘅總體(例:手上嘅股票嘅行為大概正確噉反映到古往今來所有股票嘅行為),而呢個假設喺最嚴格嘅邏輯基準嚟睇查實並唔正確(見過嘅天鵝都係白色,唔代表古往今來嘅天鵝冚唪唥都係白色)。因為呢啲原因,雖然話事實經已說明咗,機械學習喺實用上表現好好,但喺理論上機械學習嘅原理查實唔係冇漏洞嘅,所以研究運算學習論嘅科學家就要去思考呢啲問題[15]。
基本流程
[編輯]喺實用上,機械學習嘅流程基本上如下[16]:
- 搜集數據:用某啲方法搜集一啲描述緊要預測嘅現象嘅數據,並且以某啲形式(例如係一個表)呈現啲數據,數據嘅質同量會影響最後個模型嘅準確性;
- 事前處理數據:處理吓啲數據先,清走啲會擾亂機械學習演算法嘅嘢,好似啲缺失數據呀噉;
- 揀個演算法:機械學習可以用好多唔同嘅演算法嚟做,唔同演算法各有利弊;
- 訓練個 ML 程式:將啲數據輸入去個程式嗰度,等佢按自己嘅演算法建立一個模擬個現象嘅數學模型,個數學模型會有若干個參數();
- 評估個 ML 程式:用某啲指標評估個程式學得有幾好,通常嘅做法係要個程式對佢未見過嘅數據進行預測,再睇吓佢預測得準唔準;
- 執吓啲參數:執吓個程式啲參數(例如係學習率或者係初始化嘅數值等),睇吓呢啲改變可唔可以再改善個程式[註 1][註 2];
- 作出預測:用個程式對現實世界嘅現象進行預測。
事前數據處理
[編輯]
事前數據處理[e 6]係攞到數據之後要做嘅第一個步驟。喺搜集數據嘅過程之後,個研究者手上會有一個數據庫,個數據庫嘅數據包含咗每一個個案喺每個變數上嘅數值。現實嘅搜集數據過程都係唔完全受控嘅,所以搜集到嘅數據幾乎梗會出啲錯,例如係某幾個個案喺某個變數上嘅數值量度唔到(即係所謂嘅缺失數據)或者有啲擺明冇可能嘅數值(例:有個個案喺「年齡」呢個變數嘅數值係負數),等等。呢啲噉嘅數據直接攞去分析嘅話好多時會搞到個程式出錯,所以做機械學習嘅人喺開始俾個程式做學習之前往往會做啲事前處理先。另一方面,做事前數據處理又會涉及「將啲數據轉化成要用嘅機械學習能夠處理嘅格式」等嘅工序[17][18]。
以下係一段用 Python 程式語言寫嘅源碼,用途在於將啲數據重新縮放成 0 至 1 之間嘅數值(將每個變數,最大嘅數值設做 1,最細嘅數值設做 0,而喺中間嗰啲數值就按比例變成 0 至 1 之間嘅實數)。噉樣做係因為,有某啲機械學習演算法需要數據係 0 至 1 之間嘅數先至行得到[19]:
# Python code to Rescale data (between 0 and 1)
import pandas
import scipy
import numpy
from sklearn.preprocessing import MinMaxScaler
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/pima-indians-diabetes/pima-indians-diabetes.data" # 指定一個網址
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] # 指定每個變數嘅名
dataframe = pandas.read_csv(url, names=names) # 由網址嗰度攞數據。
array = dataframe.values # 將數據擺入去屬於個程式一個 array 嗰度。
X = array[:,0:8] # X 呢個 array 包含咗用嚟做預測嘅變數。
Y = array[:,8] # Y 呢個 array 包含咗要預測嘅變數。
# 將 X 入面嘅數字重新縮放。
scaler = MinMaxScaler(feature_range=(0, 1))
rescaledX = scaler.fit_transform(X)
# 將做完縮放嘅嗰柞數據 show 出嚟睇。
numpy.set_printoptions(precision=3)
print(rescaledX[0:5,:])
# 跟住打後嘅碼就會開始做學習過程。
數學模型
[編輯]喺準備好啲數據之後,個機械學習程式就要建立一個數學模型。佢要將數據當中嘅某啲變數做輸入,然後用佢內部嘅數學模型計個佢預想嘅輸出出嚟(預想輸出係啲輸入嘅函數)。喺最簡單嘅監督式學習裏面,個程式跟住會計吓,用佢個數學模型()計嘅「預想輸出」同實際嘅輸出差幾遠(睇誤差函數),按照呢個誤差調較自己個數學模型嘅參數( 係第 個參數),
- , 係指「 嘅改變」;
讀取事前處理完嘅數據;
建立一個數學模型(f),將 y(要預測嘅變數)寫成 x(用嚟做預測嘅變數)嘅函數;
逐個逐個噉讀取數據入面嘅個案,for 每一個個案
按照個數學模型同個個案嘅 x 值,計出預想嘅 y 值;
計吓「預想中嘅 y 值」同「個數據所顯示,嗰個個案嘅實際 y 值」差幾遠;
按呢個誤差,計吓個模型要點樣改;
# 如果一切順利,讀取嗮所有數據之後,最後嗰個數學模型會能夠做有返咁上下準嘅預測。
當中 可以有好多唔同款:
迴歸模型
[編輯]
迴歸分析[e 7]係統計模型上嘅一類技術,用嚟預測兩個或者以上唔同變數之間嘅關係[20]:喺統計學上,研究者好多時會想用一個變數嘅數值嚟預測第啲變數嘅數值;喺最簡單嗰種情況下,個統計模型會涉及兩個連續嘅變數,當中一個係自變數(IV),而另一個就係應變數(DV),而個研究者會用個 IV 嘅數值嚟預測個 DV 嘅數值;對個研究者嚟講,一個可能嘅做法係搜集啲數據返嚟,用啲數據做迴歸分析,整個模型(即係畫條線)出嚟,個模型就能夠幫佢預測「當 IV 係呢個數值嗰陣,假設第啲因素不變,個 DV 嘅數值會傾向係幾多」[21][22]。迴歸模型有以下呢啲[23]:
- (線性迴歸);
- (多項式迴歸);
... 等等。
原則上,如果有個方法可以搵出 同埋 等參數嘅數值,就可以靠條式大致上用 IV 嘅值估計 DV 嘅值,而機械學習可以用一個迴歸模型做佢嘅數學模型,例如係以下呢段碼噉,做嘅嘢就係(攞到數據同做完啲事前處理之後)建立一個參數值係隨機設嘅線性迴歸模型,再按柞數據入面啲個案慢慢噉調較個模型[20]。
人工神經網絡
[編輯]
人工神經網絡[e 8]係受生物神經系統啟發嘅一種數學模型[24]。一隻(例如)靈長目動物嘅腦閒閒地有斷百億計嘅神經細胞,一粒神經細胞喺俾電同化學物訊號刺激到嗰陣,會跟住以電或者化學物嚟傳新訊號,所以當一粒神經細胞射訊號嗰陣可以引起連鎖反應,將資訊喺成個神經網絡嗰度傳開去;而人工神經網絡主要係以電腦程式嘅方法嚟模擬呢個過程,令一個電腦程式能夠出現一啲好似動物神經系統噉嘅行為[25]。
一個人工神經網絡由大量嘅人工神經細胞[e 9]組成。用電腦程式整神經網絡嗰陣,個研究者(通常)會每粒人工神經細胞都同佢設返個數值,用呢個數代表佢嘅啟動程度[26],而每粒神經細胞嘅啟動程度嘅數值都有條式計,呢條式包括咗喺佢之前嗰啲神經細胞嘅啟動程度。啲函數當中嘅參數可以變化,而如果一個神經網絡嘅程式令到佢識得靠自己嘅經驗嚟到調整呢啲參數嘅話,嗰個神經網絡就會具有學習嘅能力[27][28]。
舉個例說明,例如家吓搵個神經網絡入面某一粒人工神經細胞集中睇佢,佢會有返個數字嚟反映佢嘅啟動程度,而呢個數字取決於第啲人工神經細胞嘅啟動程度-即係話個程式入面每粒細胞都會有一條類似噉樣嘅算式:
- ;
喺呢條式當中, 代表嗰粒神經細胞嘅啟動程度, 代表其他神經細胞當中第 粒嘅啟動程度,而 就係其他神經細胞當中第 粒嘅權重(指嗰粒神經細胞有幾影響到 )。所以當一粒人工神經細胞啟動嗰陣,會帶起佢後面啲人工神經細胞跟住佢啟動-似十足生物神經網絡入面嗰啲神經細胞噉。假如個神經網絡嘅程式令佢能夠自行按照經驗改變 嘅數值嘅話,佢就會曉學習[27]。
喺演算法上,一個最簡單嘅監督式學習神經網絡同一個用迴歸模型嘅機械學習演算法一個板,分別只係在於 y 同 x 之間嗰條式唔同咗。喺一個人工神經網絡嘅程式當中,會有若干粒細胞做輸出值,若干粒細胞做輸入值,每粒輸出層細胞嘅啟動程度會係佢之前嗰層細胞嘅啟動程度嘅函數,如此類推。喺程式編寫上,呢啲咁多嘅權重值同啟動值可以用矩陣輕易噉儲住。好似係以下呢段虛擬碼噉[27]:
X = [0, ...]; # 個 IV 層,呢個係一個 array(陣列)。
...
Y = A_1*H_1; # 輸出 Y 嘅啟動程度係之前嗰層嘅啟動程度嘅函數,當中 Y 同 H_1 係 array,而 A_1 係一個矩陣。
H_1 = A_2*H_2 # 如此類推如此類推
H_2 = A_3*X
# 隨機噉設啲權重嘅數值,噉做會整出一個唔準嘅迴歸模型。
A_1 = random(0,1);
A_2 = random(0,1);
A_3 = random(0,1);
...
一開始嗰陣,人工神經網絡嘅技術係諗住用嚟普遍噉解難嘅,但隨時間過去,啲人開始發覺設計上偏離生物神經網絡嘅人工神經網絡喺好多情況下能夠更加有效噉解難,於是出咗好多唔同種嘅神經網絡。到咗廿一世紀,人工神經網絡經已廣泛噉俾人用嚟教電腦辨識圖像、辨識語音、管控社交網站、做機械翻譯同埋玩遊戲[28]。
決策樹
[編輯]
決策樹學習[e 10]係機械學習嘅一種模型,一樖決策樹會有若干個節點[e 11],每個節點代表咗一個考慮緊嘅變數,並且喺接收到一個個案嗰陣,先後噉用呢啲變數作出預測,例如係附圖入面嗰個決策樹噉樣,佢會接收一個個案嘅數據,然後先後噉按照個個案嘅各種變數(性別、年紀同有幾多個親屬喺船上呀噉)預測嗰個鐵達尼號乘客有幾大機會生還。而一個用決策樹嘅機械學習演算法要做嘅嘢就係用手上嘅數據,砌出一個噉樣嘅決策樹[29]。一個建立決策樹嘅演算法步驟大致如下[30]:
例如係以下嘅虛擬碼噉,就能夠由手上數據砌一個決策樹出嚟(呢個演算法就係所謂嘅 ID3)[31][32]:
計吓成個數據庫嘅資訊熵(簡單啲講就係指柞數據有幾接近完全隨機)
For 每一個用嚟做預測嘅變數
計吓用咗佢分類之後嘅總熵
計吓用咗佢分類之後嘅總熵同成個數據庫嘅熵差幾多(zi seon gain)
揀 zi seon gain 最高嗰個變數嚟分類
For 每一個分咗嘅類,用嗰個類內嘅個案做數據庫,做多次上述嘅過程,直至用嗮所有用嚟做預測嘅變數,或者到咗指定嘅分枝數上限為止。
貝葉斯網絡
[編輯]貝葉斯網絡[e 12]係一種可以用嚟教電腦推理[33]、學習[34]、同計劃[35]嘅工具。一個貝葉斯網絡會考慮大量嘅變數,並且用一柞基於貝葉斯定理[e 13]嘅方程式模擬唔同變數之間嘅關係。舉個簡單例子說明,假想家吓有一個貝葉斯網絡,佢會睇某啲變數(包括咗有冇落雨同埋啲灌溉花灑有冇開著)嘅數值,並且計出啲草係濕嘅呢個狀態係真嘅機會率,會用到(例如)以下呢條式[36][37]:
- ;
當中 係指啲草濕咗呢個狀態, 係指啲灌溉花灑著咗呢個狀態,而 係指有落雨呢個狀態。成條式用日常用語講嘅話係噉嘅:嗰三個狀態都係真嘅機會率()等如如果有落雨而且啲灌溉花灑著咗,啲草濕咗嘅機會率()乘以如果有落雨,啲灌溉花灑著咗嘅機會率()乘以有落雨嘅機會率()。

個設計者寫好程式之後,可以(例如)走去搵一大柞有關呢幾個變數之間嘅關係嘅數據俾個程式睇,跟住叫個程式用呢啲過往嘅數據,計出變數同變數之間嘅關係係點,而個程式就可以攞嚟預測未來[36]。貝葉斯式嘅人工智能有相當廣泛嘅用途,例如 Xbox Live 噉,佢哋幫網上遊戲玩家搵比賽加入嗰陣,就會用到考慮嗰個玩家嘅贏率嘅貝葉斯網絡[38],並且寫個演算法搵出令到呢個機會率最接近 50% 嘅分隊法(即係盡可能令場比賽勢均力敵,一般認為勢均力敵嘅比賽會好玩啲)[38]。
支援向量機
[編輯]支援向量機[e 14]係一類機械學習上會用嘅數學模型,用嚟做分類,多數係監督式學習之下先會用嘅。當一個支援向量機接到收有關一柞個案嘅數據嗰陣時,會將每個個案分類做兩個(事先指定咗嘅)類別嘅其中一個。例如係下圖入面噉,黑點同白點係兩類唔同嘅個案,每個個案喺 X 軸同 Y 軸呢個變數上有個數值,H1 呢條線唔能夠將個案清楚噉分類,H2 叫勉強做到分類,而 H3 就能夠清楚噉將個案分做兩類,係最理想嗰條線-而用多個兩個變數做分類嘅支援向量機可以按同一道理想像[39][40]。

一個建立一個支援向量機嘅演算法大致上要做以下嘅工作[39]:
- 讀取數據;
- 將數據入面每一個個案用一個向量表達(; 係個個案所屬嘅類別,而 就係若干個用嚟將個案分類嘅變數);
- 喺個空間(維度數量 = 用嚟分類嘅變數嘅數量)入面畫一條線[註 4],再用某啲指標量度呢條線「能唔能夠有效噉將啲個案清楚分類」;
- 按指標睇吓使唔使改吓條線同埋要點改。
當中條線界可以係「硬性」嘅,即係非黑即白嘅二元分類,又可以係「軟性」嘅,會容許部份個案「含糊,唔知分做邊個類好」。
學習範式
[編輯]建立咗一個數學模型之後,個程式就要以某啲方法慢慢噉改變個模型啲參數-係迴歸模型或者支援向量機嘅話,就要執條線嘅式嗰啲系數;係人工神經網絡嘅話,就要執啲神經細胞之間嘅權重值... 等等,目的係最後達致一個能夠準確噉做預測同決策嘅模型-就好似人同第啲動物嘅學習過程噉樣。喺機械學習上,呢個過程可以用好多演算法做,而呢啲演算法可以分幾大類[41][42]:
監督式
[編輯]監督式學習[e 15]可以話係最簡單直接嗰種學習範式。監督式學習演算法做嘅嘢係建立一個數學模型模擬柞數據,佢當中某啲變數扮演輸入、又有啲變數扮演輸出。柞學習用嘅數據係所謂嘅訓練用數據[e 16]。用數學行話講返,即係要搵出一柞已知嘅例子,有
- 若干對輸入()同正確輸出(),,
- 再由容許得嘅函數當中搵返個同啲例子最啱搭嘅函數 出嚟。
喺呢種學習之下,個神經網絡會由研究者度收到一柞數據俾佢學,好似有個老師噉-所以就叫「監督」式學習[41][43]。
- 攞數據入面嘅一個個案(通常用一個向量表示);
- 用嗰個個案嘅「預測用變數」嘅值做自己個數學模型()嘅輸入,計自己個模型所俾嘅輸出;
- 比較自己計嗰個輸出值同埋數據顯示嘅實際輸出值(即係所謂嘅監督訊號[e 17]);
- 攞呢兩個數嘅落差(誤差),計吓自己個模型啲參數要點變,先可以令到自己下次更有可能計到正確輸出值;
- 攞數據入面嘅下一個個案做多次呢個過程,直至讀完嗮個數據入面嘅所有個案為止。
用監督式學習可以訓練一個機械學習程式做好多唔同嘅工作,好似係規律辨識呀噉[44]。舉個例說明,家吓有個研究員想訓練一個程式分辨一個病人係咪有肺癌[45],用嚟幫啲醫生手做檢查;佢可以去問醫院同醫學院等嘅單位借有關肺癌病人嘅數據,呢柞數據要包括咗每個病人嘅檢查結果()以及佢係咪真係有肺癌()等嘅資訊;跟手個研究員就會逐個逐個將啲病人個案嘅檢查結果同 X 光片嗰柞數字入落去個程式嘅輸入嗰度,而個輸出層就會係是但一個二元[e 18]嘅輸出-有肺癌(用 1 代表)同冇肺癌(用 0 代表)。初頭嗰陣,個程式會犯好多錯,但係用呢柞數據訓練到咁上下之後,個程式會根據佢啲學習法則改變咗佢啲參數,順利嘅話啲誤差會變到愈嚟愈細[46];而最後如果個誤差細到去一個可以接受嘅水平嘅話,啲醫護人員就有可能會有興趣用呢個程式幫佢哋手做肺癌檢查。事實係,喺醫學上經已有唔少醫護人員會用機械學習程式幫手做診斷,有研究甚至發現,用機械學習程式嚟做診斷有陣時仲準過用人手做[47]。
非監督式
[編輯]
非監督式學習[e 19]同監督式學習最大分別在於非監督式學習唔會有個設計者話俾個程式知乜嘢先係「正確答案」。一個用非監督式學習嘅機械學習程式淨係會接收輸入,並且嘗試由收到嘅輸入當中搵出一啲規律。一個典型嘅非監督式學習演算法嘅步驟大致如下[48]:
- 攞數據入面嘅一個個案;
- 將佢同第啲個案比較,例如係佢會唔會同某柞個案(「某柞個案」係手上個案嘅子集)有共通點或者喺各變數上嘅數值距離特別近等等;
- 將下一個個案噉樣做。
非監督式學習最常見嘅用途係攞嚟做聚類分析。譬如話,家吓有個生態學家想研究吓一柵區域入面嗰啲樹傾向於聚集喺乜嘢位置,佢可以坐直昇機或者用人造衛星影啲相返嚟,再記錄嗮嗰柵區域入面每樖樹生喺邊個位(呢個過程會嘥唔少時間),噉樣得出一個數據庫,之記錄嗮每樖樹喺 X 軸同 Y 軸嗰度嘅坐標。跟手佢就可能會想睇吓:啲樹會唔會傾向於聚集喺個區域入面嘅某啲特定位置(呢啲資訊可能有助佢保育一啲靠樹生存嘅動物)。如果相對嚟講有某一柞、啲樹彼此之間距離近、又同佢哋以外嘅樹距離遠,噉就可以話佢係「聚埋一羣」。而聚類分析就正係用嚟分析一柞個案入面會唔會有幾羣個體係「彼此之間距離近,同羣以外啲個體距離遠」嘅[49][50]。
喺呢次研究入面,個生態學家唔會事先知道要點將啲樹分羣,所以用唔到監督式學習[50]。但係佢可以使非監督式學習嚟整一個神經網絡幫佢手做呢個聚類分析。一個簡單嘅可能做法係好似以下噉:將浸輸入層設做「樖樹嘅坐標」,等啲隱藏層用每一樖樹嘅數據逐個逐個計吓。而浸輸出層就有(例如)5 粒人工神經細胞。對每樖樹嘅運算結束之後都會有一粒輸出層嘅神經細胞個啟動程度係大過其他嘅-據此個生態學家就可以按「將樖樹嘅數據入咗落去個神經網絡度之後,邊粒輸出層神經細胞嘅啟動程度最大」為準則將啲樹分做唔同聚類,而且佢仲有得按照分類結果分得好唔好,嚟計吓使唔使改變吓個神經網絡啲參數-個神經網絡就噉喺度學習。除咗噉,電腦科學界仲有第啲更加精良嘅演算法嚟做開非監督式學習[50][51]。
強化學習
[編輯]強化學習[e 20]係機械學習嘅一種學習範式,機械人設計上好有用。喺強化學習嘅過程裏面,個研究者唔會有個數據庫 俾個程式睇同跟住學,而係俾個程式係噉同佢周圍嘅環境互動(個環境可以係現場,又可以係一個模擬嘅環境):喺每一個時間點 ,個程式會產生一個用輸出數字表示嘅動作(例如 0 代表企喺度唔郁同 1 代表向前行呀噉),而跟住佢周圍個環境會俾返一啲 feedback-簡單啲講就係話返俾個程式聽,佢個動作啱唔啱(例如個地下有個窿,向前行會跌得好痛)。而個程式跟手就會根據呢個 feedback 計吓,睇吓要點樣改佢嗰啲參數先可以令到下次佢做行動嗰陣得到正面回應嘅機會率高啲-而上述嘅呢個例子就有可能可以攞嚟教一個機械人行路[52][53][54]。
- 個程式俾出一個輸出,;
- 個環境會根據佢嘅內部運作法則決定 feedback,,係乜( 係現時狀態,而 係下一個狀態);
- 個程式會根據 決定係咪要修改自己內部嘅參數,若果係,要點改;
- 返步驟 1做過。
個程式內部要有一個演算法,個演算法要用 做輸入,俾出「內部參數要變幾多」做輸出[55]。
遺傳演算法
[編輯]遺傳演算法[e 21]係一種建基於進化論物競天擇過程嘅機械學習演算法:喺進化論上,一個族群內部嘅生物個體(例如一群人類)彼此之間或多或少噉喺遺傳上有所差異,而呢啲差異會引致佢哋喺表現型(包括外表、行為同體質等)上有個體差異,當中佢哋有啲生存同繁殖嘅能力勁啲,所以就更加大機會將自己啲遺傳基因傳俾下一代。假設環境唔變,個族群就會一代一代噉遺傳出現變化,變到愈發適應到喺佢哋身處嘅環境度生存同繁衍。遺傳演算法就係受到呢個概念啟發而成嘅,主要步驟如下[57][58]:
- 整一大拃同類嘅數學模型出嚟,每個模型啲參數都有些少唔同;
- 叫每個數學模型做若干次嘅預測,每個都按佢做預測嗰陣嘅準確度得到一個分數 ,例如分數愈高表示佢「表現愈好」;
- 揀選分數 最高嗰若干個模型,其餘嗰啲模型受到淘汰;
- 做「繁殖」嘅過程-用最高分嗰柞模型做「父母」,生產下一代嘅模型。啲「仔女」喺參數上會似佢哋嘅父母(每個仔嘅每粒參數都係「佢父母嘅同位參數」嘅函數);
- 再做過上述過程,重複若干代;
如果一切順利,若干代之後手上嘅模型會係一啲預估估得啱嘅模型[59]。
模型評估
[編輯]
做完學習過程之後,就要評估吓最後得出嗰個模型好定唔好[60][61]。要評一個模型係咪「好」,有以下指標使得:
準確度
[編輯]最常用開評估機械學習模型嘅指標就係準確度[62][註 5]。即係做完學習之後,要個機械學習程式睇一啲佢之前未見過嘅個案,同埋要佢對嗰啲個案進行預測。譬如一個訓練嚟預測股價嘅機械學習程式噉,要評估佢嘅準確度,最好方法就係要佢預估吓一啲股價、係佢之前未見過嘅時間點嘅。如果個程式做嘅嘢係將個案分做離散嘅類,準確度可以用以下嘅式計:
- 係估啱咗幾多個個案;
- 係個案嘅總數。
而要評估一個模型嘅準確度,通常都要將啲數據「劏開」做幾份,用其中一啲做訓練,淨低嘅做檢驗。包括[62][63]:
- 將手上啲數據分成訓練集[e 22]同測試集[e 23],即係:開始做學習之前,將手上數據分做訓練集同測試集。用訓練集(通常包含咗 2/3 嘅個案)做學習,然之後用測試集(通常包含 1/3 嘅個案)要個程式試吓做預測,再用某啲指標嚟量度個程式喺測試當中個預測有幾準-如果係做分類嘅話,可以用準確度(估啱嘅比率)做指標;而如果要預測嘅變數係連續變數嘅話,就可以使平均誤差(平均嚟講,預測嘅數值同正確數值差幾遠)。
- 自助抽樣法[e 24];設個數據入面嘅個案數量係 n;個演算法會由啲數據度隨機抽一個個案出嚟,將個個案放入自助樣本,跟住再擺返第個個案入去抽過(即係所謂嘅邊替換邊抽樣[e 25]),重複 n 次。最尾得出一個(可能有重複嘅)自助樣本,用個自助樣本做過測試。
- K 次交叉驗證[e 26]:隨機噉將數據嘅個案劏做 K 份(喺實際應用上,K 一個常見數值係 10);然後攞其中一份做測試,其餘啲份做學習-跟住逐份逐份(每次都係一個疊代)行呢個過程。同一道理,都要使用某啲指標量度準確度。以下係 次()交叉驗證嘅抽象圖解:

靈敏同特異
[編輯]除咗預測準確度之外,如果一個模型係做二元分類嘅,模型質素亦可以用靈敏度同特異度[e 27]作為指標嚟量度。靈敏度同特異度包括咗四個數值:
- 歸啱咗啲陽性個案——真陽性率(TRP)
- 歸啱咗啲陰性個案——真陰性率(TNR)
- 歸錯咗啲陽性個案——假陽性率(FRP)
- 歸錯咗啲陰性個案——假陰性率(FNR)
當中靈敏度係講緊真陽性率有幾高。呢四個數值可以用 2 × 2 嘅混淆矩陣[e 28]表達,好似以下噉[64][65]:
| |||||||||||||
亦都有啲設計者嫌呢啲數字淨係顯示到比例,所以寫論文同報告嗰陣會將啲比例嘅分子分母都報埋出嚟[66][67]。而喺實際應用上,靈敏度同特異度相關嘅基準可以用圖表嚟表達[68],當中醫療相關研究常用嘅 ROC 曲線[e 29],打戙條軸係真陽性率而打橫條軸係假陽性率,顯示呢兩個數值喺唔同門檻值[e 30]下嘅比例,好似下圖噉:

一般嚟講,睇 ROC 曲線要睇嘅係條曲線下嘅面積有幾大。如果成幅圖都喺條曲線下面嘅,就表示個模型係完美嘅分類器:無論門檻值係幾多,個模型嘅真陽性率都係 1.0(100%)而假陽性率都係 0.0(0%) ——而條 ROC 曲線望落愈似上圖藍線,就愈表示佢接近一個完美嘅分類器[69]。
過適嘅問題
[編輯]人工智能學起嘢嗰陣好多時都會跟奧坎剃刀[e 31]嘅原則:呢條原則話,假設其他因素不變,一個學習者會偏好比較簡單啲嘅理論同假說,除非比較複雜啲嗰個模型(例如)解釋同預測現實嘅能力勁好多。
當一個人工智能(通常因為設計得唔好)學習嗰陣,為咗要令自己信嗰個模型完美符合過去數據,而選擇一個太複雜嘅模型嗰陣,呢個現象就係所謂嘅過適[e 32]:雖然話呢啲複雜嘅模型解釋過去數據嘅能力比較勁,但係統計學上嘅研究顯示,呢啲模型通常解釋將來數據嘅能力會渣啲。因為噉,用手上數據評估一個機械學習模型嗰陣,研究者通常會係想個模型嘅表現有返咁上下好,但如果個模型表現好得滯(例如準確度有成 100%),研究者往往會開始擔心有過適嘅問題[70]。
下圖係過適嘅展示。學嘢嗰陣,人工智能會嘗試搵條有返咁上下合乎過去數據(黑點)嘅線,用條線做心目嘅模型。藍色嗰條線有過適嘅問題-藍色線完美符合過去數據,但佢條式複雜過黑線好多,通常解釋將來數據嘅能力會比較渣。
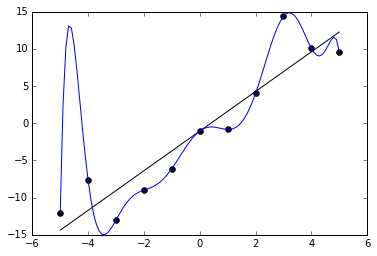
正則化[e 33]可以用嚟教電腦「唔好建立太過複雜嘅模型」,減少個模型嘅參數數量[註 6],從而紓緩過適嘅問題[71]。
主要應用
[編輯]異常檢測
[編輯]喺數據探勘上,異常檢測[e 34]係指探測一啲同手上嘅大多數個案唔同嘅異常個案,好多時係因為呢啲個案有啲可疑-例如係喺醫療上探測邊啲病人身體狀況數據異常、金融上邊啲銀行交易似係詐騙,又或者一段字入面邊啲句子似係文法錯誤啊噉。喺現實應用當中,要檢查嘅個案數量通常閒閒地都論千計,所以好難用人手做。因為噉,有唔少機械學習專家都落力研究點樣用機械學習技術做異常檢測[72][73]。
異常檢測方面嘅技術常用於探測異常網絡活動(因為呢啲活動表示可能有黑客攻擊等嘅網絡安全問題)。喺呢種情況下,異常檢測未必會依賴異常作為分類指標,因為呢啲活動未必咁罕有;一種常見嘅做法係運用聚類分析,教部電腦(例如)認出同黑客攻擊有拏褦嘅網絡活動通常都有啲乜嘢特徵,最後令部電腦曉自動噉探測邊啲活動似係黑客攻擊[74][75]。
無論監督式學習定非監督式學習,機械學習演算法都可以攞嚟做異常檢測。非監督式學習嘅例子通常係,個程式自動噉用聚類分析將啲個案分類、再自動噉將啲屬於少數類型嘅個案歸類做異常。呢種做法大前題係啲屬少數嗰類型嘅個案真係想要探測嘅類型(喺網絡安全上,呢條假設未必成立)。而監督式學習嘅例子通常嚟講就係個程式設計者明文噉教個程式,講埋佢聽邊啲個案係異常,邊啲係正常。半監督式學習嘅做法就係用一柞正常個案嘅數據,建立一個數學模型;撞到下一個個案嗰陣,計吓「假設個產生個案嘅模型同程式內部嗰個一樣、會出現呢啲數值」嘅機會率。而假如計出嚟呢個機會率數值夠細,就有理由相信呢個個案屬於異常[74][76][77]。
推薦系統
[編輯]推薦系統[e 35]指一個曉預測用家對某件物件會俾乜評價嘅系統,當中成日會用到機械學習演算法。推薦系統嘅例子有 YouTube 等影片分享平台會做嘅「向用家推介有啲乜片佢會有興趣睇」或者 Google 搜尋等嘅搜尋器會做嘅「向用家推介有啲乜新聞佢會有興趣睇」-呢啲技術基本原理都係一樣,涉及個程式攞有關用家以前睇過乜片或者乜網站等嘅資訊,預測個用家對唔同影片或者網站會有乜評價[78][79]。
喺最基本嗰種協同過濾[e 36]做法如下:協同過濾淨係攞有關個用家同啲物件嘅過去互動嘅數據做分析,想像以下呢段噉嘅演算法[78]:
import graphlab
import pandas as pd # 攞要用嘅 library
# 攞數據;呢個演算法用嘅數據包括每個用家對每件嘢食嘅評價,喺現實應用當中,評價可以用對影片嘅 like 等指標量度。
r_cols = ['user_id', 'food_item', 'rating']
train_data_df = pd.read_csv('train_data.csv', sep='\t', names=r_cols)
test_data_df = pd.read_csv('test_data.csv', sep='\t', names=r_cols)
train_data = graphlab.SFrame(train_data_df)
test_data = graphlab.SFrame(test_data_df)
# 訓練一個模型,例如整個迴歸模型,搵用家嘅特性(性別、年紀同睇開乜嘢網站等)做 x,佢對某件嘢食嘅評價做 y。
collab_filter_model = graphlab.item_similarity_recommender.create(train_data,
user_id='user_id',
item_id='food_item',
target='rating',
similarity_type='cosine')
# 當有一個用家撳 search 嗰陣,向佢推薦佢最有可能會俾高評價嘅嘢食。
which_user_ids = [1, 2, 3, 4]
how_many_recommendations = 5
item_recomendation = collab_filter_model.recommend(users=which_user_ids,
k=how_many_recommendations)
第啲應用
[編輯]機械學習能夠令電腦自動噉預測某啲變數嘅數值,所以基本上任何科學或者商學領域都可以用到機械學習嘅技術[8]:
... 等等。
學術研究
[編輯]有好多研究者都著力做機械學習研究,思考點先可以令機械學習更加有效率。機械學習研究一種簡單做法係噉嘅:研究者可以去搵個數據庫返嚟,將個數據庫嘅個案斬做兩份,一份做訓練集,另一份做測試集,然後用每個研究緊嘅演算法做訓練同埋評估表現嘅過程,比較吓呢啲演算法嘅表現係點[80][81]。
另一方面,又有啲機械學習研究會用一個研究者已知嘅數學模型嚟產生數據,然後再喺產生嘅數據上用個演算法做學習,睇吓最後個演算法俾嗰個數學模型有幾似原裝嗰個,即係行好似噉樣嘅虛擬碼[82]:
有一個已知嘅數學模型產生數據;
# 例:
# x = rand(100,1) (x 係一個向量,包含 100 個隨機產生嘅數字)
# y = rand(100,1) (set y 做 100 個數字嘅隨機向量先)
# for ii < 100 (for 每個 y 入面嘅數值,將嗰個數值設做 x 嘅相應數值嘅兩倍;y = x * 2 就係個已知嘅數學模型)
# y(ii) = x(ii) * 2
# ii = ii + 1
用 x 同 y 做數據嘅輸入同輸出,將一個監督式學習嘅 ML 演算法行一次;
最後個程式應該會有個由學習產生嘅數學模型,將個數學模型同個已知嘅數學模型比較;
如果學習產生嘅數學模型同個已知數學模型相近,表示個演算法能夠有效噉做學習。
# 然後研究者可以比較吓唔同演算法邊個最能夠準確噉學到個真嘅數學模型。
上述呢啲研究令學界能夠不斷創造更新更強嘅機械學習演算法[8][83][84]。
事實係,雖然機械學習係一種重大嘅革新,但喺應用上,機械學習好多時都達唔到理想嘅效果[85][86][87]。原因可以有好多:數據本身嘅偏差同埋用錯演算法等都可以搞到個機械學習演算法失敗[88]。「機械學習可能失敗」係一個好受關注嘅議題,因為廿一世紀初好多技術都係靠機械學習做嘅。例如係喺 2018 年,優步架靠機械學習訓練嘅自駕車探測唔到行人,於是炒咗車,仲撞死咗人[89]。而仲有個案報告話用嚟做醫療診斷嘅機械學習程式出咗錯,搞到病人好長手尾[90][91]。呢啲噉嘅問題令到機械學習嘅專家開始思考機械學習有啲乜嘢缺陷,同埋啲缺陷要點補救[85][92]。
相關領域
[編輯]
睇埋
[編輯]文獻
[編輯]英文文獻:
- Nils J. Nilsson, Introduction to Machine Learning(英文機械學習入門)
- Pedro Domingos (September 2015), The Master Algorithm, Basic Books, ISBN 978-0-465-06570-7
- David J. C. MacKay. Information Theory, Inference, and Learning Algorithms. Cambridge: Cambridge University Press, 2003. ISBN 0-521-64298-1
- Richard O. Duda, Peter E. Hart, David G. Stork (2001) Pattern classification (2nd edition), Wiley, New York, ISBN 0-471-05669-3.
- Christopher Bishop (1995). Neural Networks for Pattern Recognition, Oxford University Press. ISBN 0-19-853864-2.
- Ray Solomonoff, An Inductive Inference Machine, A privately circulated report from the 1956 Dartmouth Summer Research Conference on AI.
- VanderPlas, J. (2016). Python data science handbook: essential tools for working with data. O'Reilly Media, Inc.
註釋
[編輯]詞彙
[編輯]外語(預設係英文)詞彙:
- ↑ Alan Turing
- ↑ generalize
- ↑ probability distribution
- ↑ normal distribution
- ↑ computational learning theory
- ↑ data preprocessing
- ↑ regression analysis
- ↑ artificial neural network
- ↑ artificial neuron
- ↑ decision tree learning
- ↑ node
- ↑ Bayesian network
- ↑ Bayes' Theorem
- ↑ support vector machines,簡稱 SVM
- ↑ supervised
- ↑ training data
- ↑ supervisory signal
- ↑ binary
- ↑ unsupervised
- ↑ reinforcement learning
- ↑ genetic algorithm,簡稱 GA
- ↑ training set
- ↑ test set
- ↑ bootstrapping
- ↑ sampling with replacement
- ↑ K-fold cross-validation
- ↑ sensitivity and specificity
- ↑ confusion matrix
- ↑ receiver operating characteristic curve
- ↑ threshold
- ↑ Occam's razor
- ↑ overfitting
- ↑ regularization
- ↑ anomaly detection
- ↑ recommendation system
- ↑ collaborative filtering
引咗
[編輯]- ↑ AI today and tomorrow is mostly about curve fitting, not intelligence. diginomica.
- ↑ The definition "without being explicitly programmed" is often attributed to Arthur Samuel, who coined the term "machine learning" in 1959, but the phrase is not found verbatim in this publication, and may be a paraphrase that appeared later. Confer "Paraphrasing Arthur Samuel (1959), the question is: How can computers learn to solve problems without being explicitly programmed?" in Koza, John R.; Bennett, Forrest H.; Andre, David; Keane, Martin A. (1996). Automated Design of Both the Topology and Sizing of Analog Electrical Circuits Using Genetic Programming. Artificial Intelligence in Design '96. Springer, Dordrecht. pp. 151–170.
- ↑ 3.0 3.1 3.2 3.3 Bishop, C. M. (2006), Pattern Recognition and Machine Learning, Springer.
- ↑ 6 Top Applications of Machine Learning. Hackernoon.
- ↑ Kononenko, I. (2001). Machine learning for medical diagnosis: history, state of the art and perspective. Artificial Intelligence in medicine, 23(1), 89-109.
- ↑ Heaton, J. B., Polson, N. G., & Witte, J. H. (2017). Deep learning for finance: deep portfolios. Applied Stochastic Models in Business and Industry, 33(1), 3-12.
- ↑ Ling, C. X., & Li, C. (1998, August). Data mining for direct marketing: Problems and solutions. In Kdd (Vol. 98, pp. 73-79).
- ↑ 8.0 8.1 8.2 Friedman, Jerome H. (1998). "Data Mining and Statistics: What's the connection?". Computing Science and Statistics. 29 (1): 3-9.
- ↑ Samuel, Arthur (1959). "Some Studies in Machine Learning Using the Game of Checkers". IBM Journal of Research and Development. 3 (3): 210-229.
- ↑ 10.0 10.1 Mitchell, T. (1997). Machine Learning. McGraw Hill. p. 2,英文原文:"A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E."
- ↑ 11.0 11.1 Harnad, S. (2006). The annotation game: On Turing (1950) on computing, machinery, and intelligence. In The Turing test sourcebook: philosophical and methodological issues in the quest for the thinking computer. Kluwer.
- ↑ Walker, J. E.; Shea, T. M.; Bauer, A.M. "Generalization and the Effects of Consequences | Education.com". www.education.com.
- ↑ Vidyasagar, M. (2002). A theory of learning and generalization. Springer-Verlag.
- ↑ 14.0 14.1 Mohri, Mehryar; Rostamizadeh, Afshin; Talwalkar, Ameet (2012). Foundations of Machine Learning. USA, Massachusetts: MIT Press.
- ↑ Angluin, D. 1992. Computational learning theory: Survey and selected bibliography. In Proceedings of the Twenty-Fourth Annual ACM Symposium on Theory of Computing (May 1992), pages 351–369.
- ↑ Frameworks for Approaching the Machine Learning Process. KDnuggets.
- ↑ Pyle, D., 1999. Data Preparation for Data Mining. Morgan Kaufmann Publishers, Los Altos, California.
- ↑ Chicco D (December 2017). "Ten quick tips for machine learning in computational biology". BioData Mining. 10 (35): 1–17.
- ↑ Data Preprocessing for Machine learning in Python 互聯網檔案館嘅歸檔,歸檔日期2019年7月6號,..
- ↑ 20.0 20.1 Linear Regression with example. Towards Data Science.
- ↑ Seber, G. A., & Lee, A. J. (2012). Linear regression analysis (Vol. 329). John Wiley & Sons.
- ↑ YangJing Long (2009). "Human age estimation by metric learning for regression problems". Proc. International Conference on Computer Analysis of Images and Patterns: 74–82.
- ↑ Regression in Machine Learning. Towards Data Science.
- ↑ Gardner, M. W., & Dorling, S. R. (1998). Artificial neural networks (the multilayer perceptron)—a review of applications in the atmospheric sciences. Atmospheric environment, 32(14-15), 2627-2636.
- ↑ Russell, Stuart J.; Norvig, Peter (2010). Artificial Intelligence A Modern Approach. Prentice Hall. p. 578.
- ↑ The Machine Learning Dictionary - activation level 互聯網檔案館嘅歸檔,歸檔日期2018年8月26號,..
- ↑ 27.0 27.1 27.2 Learning process of a neural network 互聯網檔案館嘅歸檔,歸檔日期2021年2月11號,.. Towards Data Science.
- ↑ 28.0 28.1 Honglak Lee, Roger Grosse, Rajesh Ranganath, Andrew Y. Ng. "Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations" Proceedings of the 26th Annual International Conference on Machine Learning, 2009.
- ↑ Decision Trees in Machine Learning. Towards Data Science.
- ↑ Decision Tree. Machine Learning.
- ↑ Chapter 4: Decision Trees Algorithms.
- ↑ Decision Trees: ID3 Algorithm Explained. Towards Data Science.
- ↑ Bayesian inference algorithm:
- Russell & Norvig 2003, pp. 504–519,
- Poole, Mackworth & Goebel 1998, pp. 361–381,
- Luger & Stubblefield 2004, pp. ~363–379,
- Nilsson 1998, chpt. 19.4 & 7.
- ↑ Bayesian learning and the expectation-maximization algorithm:
- Russell & Norvig 2003, pp. 712–724,
- Poole, Mackworth & Goebel 1998, pp. 424–433,
- Nilsson 1998, chpt. 20.
- ↑ Bayesian decision theory and Bayesian decision networks:
- Russell & Norvig 2003, pp. 597–600.
- ↑ 36.0 36.1 Bayesian Networks 互聯網檔案館嘅歸檔,歸檔日期2019年7月9號,.. Bayesialab.
- ↑ Bayesian networks:
- Russell & Norvig 2003, pp. 492–523,
- Poole, Mackworth & Goebel 1998, pp. 361–381,
- Luger & Stubblefield 2004, pp. ~182–190, ≈363–379,
- Nilsson 1998, chpt. 19.3–4.
- ↑ 38.0 38.1 Delalleau, O., Contal, E., Thibodeau-Laufer, E., Ferrari, R. C., Bengio, Y., & Zhang, F. (2012). Beyond skill rating: Advanced matchmaking in ghost recon online. IEEE Transactions on Computational Intelligence and AI in Games, 4(3), 167-177.
- ↑ 39.0 39.1 Cortes, Corinna; Vapnik, Vladimir N. (1995). "Support-vector networks". Machine Learning. 20 (3): 273–297.
- ↑ Ben-Hur, Asa; Horn, David; Siegelmann, Hava; and Vapnik, Vladimir N.; "Support vector clustering"; (2001); Journal of Machine Learning Research, 2: 125–137.
- ↑ 41.0 41.1 Ojha, Varun Kumar; Abraham, Ajith; Snášel, Václav (2017-04-01). "Metaheuristic design of feedforward neural networks: A review of two decades of research". Engineering Applications of Artificial Intelligence. 60: 97–116.
- ↑ Ting Qin, et al. "A learning algorithm of CMAC based on RLS." Neural Processing Letters 19.1 (2004): 49–61.
- ↑ M.R. Smith and T. Martinez (2011). "Improving Classification Accuracy by Identifying and Removing Instances that Should Be Misclassified". Proceedings of International Joint Conference on Neural Networks (IJCNN 2011). pp. 2690–2697.
- ↑ Looney, C. G. (1997). Pattern recognition using neural networks: theory and algorithms for engineers and scientists (pp. 171-172). New York: Oxford University Press.
- ↑ Cancer Detection - MATLAB Example[失咗效嘅鏈].
- ↑ Menéndez, L. Á., de Cos Juez, F. J., Lasheras, F. S., & Riesgo, J. Á. (2010). Artificial neural networks applied to cancer detection in a breast screening programme. Mathematical and Computer Modelling, 52(7-8), 983-991.
- ↑ Milani, C., & Jadavji, N. M. (2017). Solving cancer: The use of artificial neural networks in cancer diagnosis and treatment. Journal of Young Investigators, 33(4).
- ↑ Jordan, Michael I.; Bishop, Christopher M. (2004). "Neural Networks". In Allen B. Tucker (ed.). Computer Science Handbook, Second Edition (Section VII: Intelligent Systems). Boca Raton, Florida: Chapman & Hall/CRC Press LLC.
- ↑ Unsupervised learning - MathWorks.
- ↑ 50.0 50.1 50.2 Unsupervised Learning and Data Clustering. Towards Data Science.
- ↑ Dostál, P., & Pokorný, P. (2009). Cluster analysis and neural network. In 17th Annual Conference Proceedings on Technical Computing Prague (pp. 131-57).
- ↑ Dominic, S.; Das, R.; Whitley, D.; Anderson, C. (July 1991). "Genetic reinforcement learning for neural networks". IJCNN-91-Seattle International Joint Conference on Neural Networks. Seattle, Washington, USA: IEEE.
- ↑ Hoskins, J.C.; Himmelblau, D.M. (1992). "Process control via artificial neural networks and reinforcement learning". Computers & Chemical Engineering. 16 (4): 241–251.
- ↑ Bertsekas, D.P.; Tsitsiklis, J.N. (1996). Neuro-dynamic programming. Athena Scientific. p. 512.
- ↑ 55.0 55.1 NEURAL NETWORKS AND REINFORCEMENT LEARNING 互聯網檔案館嘅歸檔,歸檔日期2018年10月24號,. (PDF).
- ↑ Miller, W. T., Werbos, P. J., & Sutton, R. S. (Eds.). (1995). Neural networks for control. MIT press.
- ↑ Goldberg, David E.; Holland, John H. (1988). "Genetic algorithms and machine learning". Machine Learning. 3 (2): 95-99.
- ↑ Michie, D.; Spiegelhalter, D. J.; Taylor, C. C. (1994). "Machine Learning, Neural and Statistical Classification". Ellis Horwood Series in Artificial Intelligence.
- ↑ Zhang, Jun; Zhan, Zhi-hui; Lin, Ying; Chen, Ni; Gong, Yue-jiao; Zhong, Jing-hui; Chung, Henry S.H.; Li, Yun; Shi, Yu-hui (2011). "Evolutionary Computation Meets Machine Learning: A Survey" (PDF). Computational Intelligence Magazine. 6 (4): 68-75.
- ↑ Metrics to Evaluate your Machine Learning Algorithm. Towards Data Science.
- ↑ Various ways to evaluate a machine learning model’s performance. Towards Data Science.
- ↑ 62.0 62.1 Kohavi, Ron (1995). "A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection". International Joint Conference on Artificial Intelligence.
- ↑ Rodriguez, J. D., Perez, A., & Lozano, J. A. (2009). Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE transactions on pattern analysis and machine intelligence, 32(3), 569-575.
- ↑ Provost, Foster; Fawcett, Tom (2013). Data science for business: what you need to know about data mining and data-analytic thinking (1. ed., 2. release ed.). Beijing Köln: O'Reilly.
- ↑ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer.
- ↑ Altman DG, Bland JM (June 1994). "Diagnostic tests. 1: Sensitivity and specificity". BMJ. 308 (6943): 1552.
- ↑ Pontius, Robert Gilmore; Si, Kangping (2014). "The total operating characteristic to measure diagnostic ability for multiple thresholds". International Journal of Geographical Information Science. 28 (3): 570-583.
- ↑ (英文) Understanding Gain Chart and Lift Chart,呢篇文講到用 Gain Chart 同 Lift Chart 嚟評估 ML 模型。
- ↑ Classification: ROC and AUC. Google for Developers.
- ↑ Domingos 2015, Chapter 6, Chapter 7.
- ↑ (英文) 乜嘢係正規化?,IBM
- ↑ Killourhy, K. S., & Maxion, R. A. (2009, June). Comparing anomaly-detection algorithms for keystroke dynamics. In 2009 IEEE/IFIP International Conference on Dependable Systems & Networks (pp. 125-134). IEEE.
- ↑ Zimek, Arthur; Schubert, Erich (2017), "Outlier Detection", Encyclopedia of Database Systems, Springer New York, pp. 1–5.
- ↑ 74.0 74.1 Hodge, V. J.; Austin, J. (2004). "A Survey of Outlier Detection Methodologies". Artificial Intelligence Review. 22 (2): 85–126.
- ↑ Dokas, Paul; Ertoz, Levent; Kumar, Vipin; Lazarevic, Aleksandar; Srivastava, Jaideep; Tan, Pang-Ning (2002). "Data mining for network intrusion detection" (PDF). Proceedings NSF Workshop on Next Generation Data Mining.
- ↑ Chandola, V.; Banerjee, A.; Kumar, V. (2009). "Anomaly detection: A survey". ACM Computing Surveys. 41 (3): 1–58.
- ↑ Mahadevan, V., Li, W., Bhalodia, V., & Vasconcelos, N. (2010, June). Anomaly detection in crowded scenes. In 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (pp. 1975-1981). IEEE.
- ↑ 78.0 78.1 An Easy Introduction to Machine Learning Recommender Systems.
- ↑ Davidson, J., Liebald, B., Liu, J., Nandy, P., Van Vleet, T., Gargi, U., ... & Sampath, D. (2010, September). The YouTube video recommendation system. In Proceedings of the fourth ACM conference on Recommender systems (pp. 293-296).
- ↑ Baluja, S., & Pomerleau, D. (1994). Non-intrusive gaze tracking using artificial neural networks. In Advances in Neural Information Processing Systems (pp. 753-760).
- ↑ Foody, G. M., McCulloch, M. B., & Yates, W. B. (1995). The effect of training set size and composition on artificial neural network classification. International Journal of Remote Sensing, 16(9), 1707-1723.
- ↑ Lange, K. L., Little, R. J., & Taylor, J. M. (1989). Robust statistical modeling using the t distribution. Journal of the American Statistical Association, 84(408), 881-896.
- ↑ Acerbi, L., & Ji, W. (2017). Practical Bayesian optimization for model fitting with Bayesian adaptive direct search. In Advances in neural information processing systems (pp. 1836-1846).
- ↑ Lüthi, M., Jud, C., & Vetter, T. (2013, September). A unified approach to shape model fitting and non-rigid registration. In International workshop on machine learning in medical imaging (pp. 66-73). Springer, Cham.
- ↑ 85.0 85.1 "Why Machine Learning Models Often Fail to Learn: QuickTake Q&A". Bloomberg.com.
- ↑ "The First Wave of Corporate AI Is Doomed to Fail". Harvard Business Review. 2017-04-18.
- ↑ "Why the A.I. euphoria is doomed to fail". VentureBeat. 2016-09-18.
- ↑ "9 Reasons why your machine learning project will fail". www.kdnuggets.com.
- ↑ "Why Uber's self-driving car killed a pedestrian". The Economist.
- ↑ "IBM's Watson recommended 'unsafe and incorrect' cancer treatments - STAT". STAT.
- ↑ Hernandez, Daniela; Greenwald, Ted (2018-08-11). "IBM Has a Watson Dilemma". Wall Street Journal.
- ↑ Char, D. S.; Shah, N. H.; Magnus, D. (2018). "Implementing Machine Learning in Health Care—Addressing Ethical Challenges". New England Journal of Medicine. 378 (11): 981–983.













































