決策樹學習

決策樹學習(粵拼:kyut3 caak3 syu6 hok6 zaap6)係一系列建立決策樹嘅機械學習做法。決策樹係一種用樹狀圖做決策嘅做法。一樖決策樹會有若干個節點,每個節點代表一個決策點,會掕住若干條線指向下一排節點,每條線表示「如果揀咗呢個選項,就去呢個決策點」[1]。
決策樹學習就係一系列嘅機械學習演算法。呢啲演算法會睇過往嘅數據,靠數據建立決策樹,提供以下嘅資訊:「由手上嘅數據睇,啲個案可以按邊啲變數(決策點)嚟分類呢?」建立咗決策樹之後,分析者就可以攞住樖決策樹,預測將來遇到嘅個案要點分類。呢種噉嘅技術,可以用嚟教人工智能做睇病(將病人分類做有病同冇病兩類)等嘅工作。
基本概念
[編輯]一樖決策樹[e 1]以根節點[e 2]為起始,根節點下會有若干排節點[e 3],是但攞一個節點嚟睇,佢都會連住若干個子節點[e 4],啲子節點喺下一排。喺概念上,每一個節點都可以當係一個決策點[e 5],而由一個節點去佢嘅子節點嘅連繫,就可以當做「如果揀咗呢個呢個選項,世界嘅狀態就變去呢個呢個節點」。
想像下圖嗰樖英文決策樹:
- 個決策者家陣想決定「好唔好去玩」(PLAY),
- 喺開頭個節點,去玩(play)嘅價值有 9 分,唔好去玩(don't play)嘅價值有 5 分,
- 然後睇天氣(OUTLOOK),如果晴天(sunny),噉去玩嘅價值變成 2 分,唔好去玩嘅價值變成 3 分,
- 然後個決策者會睇濕度(HUMIDITY)
... 如此類推[1]。如是者,分析者就做到將決策嘅過程圖像化噉展示出嚟,可以去(例如)將決策方法教畀啲下屬知。

建立方法
[編輯]決策樹學習做緊嘅嘢,就係
靠住手上嘅數據,搵出啲個案可以點分類,再建立一樖決策樹,攞住樖決策樹嘅人或者人工智能就可以做類似噉嘅判斷:「如果第時有個前所未見嘅個案喺變數 A 上嘅數值係噉噉噉,將佢分類做 x 類物件,否則就將佢分做 y 類物件,跟住再睇變數 B,睇吓一件屬 x 類嘅物件可以分做 x1 類定 x2 類...」。
|
想像而家手上有個數據庫,紀錄咗數據入面每一個個體嘅身高、體重、成績、性格(包括外向度等嘅多個特質)... 等嘅多個特性。研究者想靠呢啲數據建立一樖決策樹,將來用嚟預測啲人嘅行為。
資訊熵
[編輯]資訊熵[e 6]呢個概念,建立決策樹嘅演算法成日都會用到。資訊熵呢個概念出自資訊理論,衝量一件事「有幾大嘅不確定性喺入便」:搵一個變數嚟睇,佢會有一啲可能數值,例如「某年某月某日某刻,掟某一個銀仔」嘅可能數值大致有兩個-公同字。每個數值都會有一定機率出現,想像而家已知每一個可能數值出現嘅機率[註 1],件事件帶有嘅資訊熵(數學符號係 )可以用以下呢條式嚟計[3]:
喺呢條式當中, 係指第 i 個可能性發生嘅機率,而 係 以 2 做基數嘅對數。用呢條式計嘅話,「掟一粒冇出千嘅銀仔」(公同字出現嘅機率都係 50%)呢件事當中帶有嘅資訊熵量()就係[4]:
例如一件肯定嘅事件係無資訊熵嘅——如果其中一個可能性機率係 1(即係其他可能性機率冚唪唥等如 0),資訊熵條式會出 0,而另一方面,如果每個可能性機率都一樣(不確定性最大化)嗰陣,條式畀嘅數值亦會最大化[5]。
資訊熵可以用嚟衝量「提供到幾多資訊」——資訊熵下降反映不確定性下降。
ID3 系
[編輯]| 病人 | 有燒? | 有咳? | 中咗? |
|---|---|---|---|
| 00001 | 有 | 有 | 係 |
| 00002 | 冇 | 冇 | 唔係 |
| 00003 | 冇 | 有 | 唔係 |
| 00004 | 有 | 冇 | 係 |
| ... | ... | ... | ... |
ID3(英文全名[e 7]係疊代二分器 3 噉嘅意思)可以話係最簡單最基礎嗰款決策樹建立法,源於 1986 年。ID3 呢種演算法採用貪心搜尋——喺建立每一個節點嗰陣,呢段演算法都會睇勻晒所有可以用嚟做預測嘅變數[註 3],然後就可以想像以下噉嘅步驟[6]:p 14:
- Input:某一個目標(想預測嘅)變數 ,同埋若干個用嚟做預測嘅變數 ;
- 將 入便嘅變數逐個逐個攞晒來睇;
- 由呢啲變數當中,揀出「最能夠提升有關 嘅資訊」嗰個,嗌呢個變數做 ;
- 將啲個案,按照佢哋喺 上嘅數值分組,分做 ... 等;
- 用 嚟做新嘅「根點」, 唔再係 嘅一員,由 ... 等各「生一樖新嘅子樹」;
- 同每一樖子樹,返去做步驟 2 至 5 嘅嘢(遞歸[e 8])。
舉個實際應用例子,想像依家要將手上嘅病人分類,數據庫入面有一個個病人個案,每個個案(1 2 3 4...)都記錄咗嗰位病人「有冇發燒」、「有冇見咳」同埋「係咪真係中咗新型流感」... 等嘅資訊。研究者跟住就叫部電腦用 ID3 建立決策樹,用嚟將啲病人分類,部電腦做嘅嘢可以想像成[7]
- 將啲可以用嚟分類嘅變數—「有冇發燒」、「有冇見咳」—逐個逐個攞嚟睇,睇吓邊個最能夠令資訊熵下降;
- 例如家陣發覺「有冇發燒」係最能夠令資訊熵下降嘅,將班病人按「有冇發燒」嚟分做兩大組[註 4];
- 同每一個子節點,搵下一個可以用嚟分類嘅變數;
- 一路遞歸,直至可以用嚟分類嘅變數用晒為止。
最後得出嘅決策樹,就會容許研究者作出類似噉嘅決策過程:「首先,睇吓手上嗰位病人有冇發燒;如果有發燒,就睇吓佢有冇咳,如果有...(省略);而如果冇發燒,就睇吓佢唞氣有冇困難,如果有...(省略)」,而最後樖決策樹就會畀出「手上嗰位病人係咪中咗流感」嘅判斷。而有咗呢一樖決策樹,研究者就可以例如教 AI 做睇病嘅工作[8]。
ID3 呢種演算法畀人詬病,話佢太容易受到可能數值嘅數量影響,傾向偏好一啲「有好多唔同可能數值」嘅變數——噉即係表示 ID3 成日會重用(例如)電話號碼等「個個人數值都唔同,但攞嚟分類冇咩用」嘅變數。呢點喺某啲應用上會造成問題,而 C4.5(同埋及後嘅 C5.0)可以算係 ID3 嘅延伸版本,針對 ID3 嘅呢種漏洞嚟進行改良[6]。
CART
[編輯]CART [e 9]係另一種廿一世紀初常用嘅決策樹建立法,只能夠用嚟建立二元嘅決策樹。「二元」意思係指 CART 整出嚟嘅決策樹喺每個節點只有兩個可能選擇,唔似得 C5.0 噉可以一個節點有三個或者以上嘅選擇:例如 CART 只能夠將溫度分做凍同熱(切割點可能係攝氏 20 度),而 C5.0 整出嚟嘅決策樹就有可能將溫度分做凍、暖同熱(切割點可能係例如攝氏 30 度同攝氏 10 度)——唔係二元咁簡單[6][9]。
CART 個做法同 ID3 相關嘅演算法好相似,都係有一個目標(要預測嘅)變數,同埋一拃用嚟做預測嘅變數。段演算法會有準則決定「呢步要用邊一個預測變數嚟將啲個案分割」,然後遞歸式噉做,最後出到一樖決策樹。CART 最與別不同嘅地方,係佢用另一套方法嚟衡量「要點樣選擇用嚟做分割嘅變數」—— CART 用嘅係所謂嘅堅尼指數[e 10]:
籠統啲噉講,堅尼指數可以想像成係量度緊「純潔度」,數值係越低越好。詳細啲講:如果某個樣本入便淨係得某個可能性嘅發生機率係 1(其他可能性嘅發生機率冚唪唥都係 0)堅尼指數就會去到 0 呢個最細數值。
注意事項
[編輯]用決策樹分析數據有好多好處:首先呢種分析方法被指係可詮釋度高,唔似得(例如)人工神經網絡噉「無法解釋」;此外,決策樹分析彈性大,無論連續定係離散嘅變數佢都處理得到,亦處理到有缺失數據嘅 data;而且決策樹分析唔會假設啲數據跟啲乜嘢特定嘅概率分佈,就算啲數據(例如)唔跟常態分佈[註 5]都用得決策樹。不過要用決策樹嚟做分析,遠遠唔只要建立樖決策樹咁簡單。事前事後都有好多嘢要諗過度過先。
決策樹嘅一個問題係,佢被指容易出現過適[e 11]嘅情況[10]:原則上,高度複雜嘅決策樹模型解釋手上數據嘅能力會勁啲,但係統計相關嘅研究表明,呢啲模型解釋將來數據嘅能力通常會較弱,想像下圖噉嘅情況——
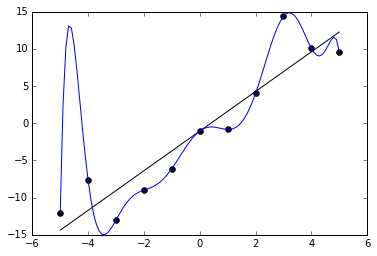
而家研究者想分析兩個變數(圖中嘅 X 軸同 Y 軸)之間成咩關係,等自己將來可以由 X 嘅值預測 Y 嘅值;佢要做嘅係嘗試搵一條有返咁上下合乎數據(每個黑點係一個個案)嘅線,用呢條線做佢心目「兩個變數之間成咩關係」嘅模型;藍色條線有過適嘅問題——藍色線係就係完美符合手上數據,但佢條式複雜過直線嘅好多,而實證研究顯示,條線咁複雜,解釋將來數據嘅能力通常會弱啲。
要防範過適,分析者通常會做吓剪枝[e 12] ——即係有技巧噉「將樖樹嘅其中一啲節點剪走佢」,減低一樖決策樹嘅複雜度。研究者可以事前剪[e 13],即係(例如)行演算法建立決策樹之前,就講定樖樹最多可以有幾層節點,又可以指定一塊「葉」起碼要有幾多個個案;又可以事後剪[e 14],試吓攞走其中一條分枝,睇吓攞走咗會唔會影響分類嘅準確度,唔會嘅話就真係攞走嗰條分枝佢... 等等[11]。
重要參數
[編輯]喺 R 程式語言等嘅工具當中,建立決策樹可以設定以下呢啲參數[12]:
maxdepth(最大深度):樖決策樹「最多可以有幾多層」,設定呢個數值就會限住由根節點去到最尾嘅葉節點「最長可以有幾遠」。minsplit(最小分割):一塊「葉」最少要有幾多個個案先可以「斬出嚟」自成一塊葉,例如呢個參數設咗做 10,部電腦要做一吓切割將啲個案分做兩份嗰陣,兩邊都要最少有 10 個個案,先至可以做切割。minbucket(最細桶量):一塊「終結葉」(佢後面冇再分支嘅葉)最少要有幾多個個案,例如呢個參數設咗做 5,部電腦做切割嗰陣會確保每一塊終結葉最少要有 5 個個案。有一種諗法認為,呢個參數數值太細容易引致過適嘅問題。- 每吓切割,個表現指標最少要改善幾多
等等。
睇埋
[編輯]- 隨機森林[e 15]:一種集成學習做法,畀若干樖決策樹「齊齊做預測」——想像而家隨機抽一拃數據(個案或者變數)出嚟,用呢拃數據建立一樖決策樹,重複 次建立 咁多樖決策樹[註 6];及後對新個案做預測嗰陣,都畀呢 樖決策樹「投票」,即係每樖決策樹各自對新個案做預測,然後就以某啲方式結合呢啲唔同預測,再畀出嚟做結果,例如要做分類而 ,呢啲決策樹當中有 3 樖都將個新個案歸類做 A 類,研究者就當個新個案係 A 類[13]。隨機森林呢種做法被指可以提高預測嘅準確度,但係就完全只顧做預測,放棄晒詮釋能力。
- 提升決策樹[e 16]:呢種做法係建立一樖決策樹先,然後再用頭嗰樖決策樹嘅殘差嚟訓練下一樖決策樹,如果有其中一拃數據係之前嗰樖決策樹零舍唔擅長預測嘅,噉呢啲數據會比較大機會成為下一樖決策樹嘅訓練用數據;同隨機森林明顯唔同嘅係,一個隨機森林入便唔同決策樹用唔同數據做訓練,而其中一樖決策樹用咩數據做訓練,係獨立於其他決策樹用咩數據嘅[14]。
- 聚類分析(等級法)
- 樹狀數據
- 人工智能
註解
[編輯]引述
[編輯]- ↑ decision tree
- ↑ root node
- ↑ node
- ↑ child node
- ↑ decision point
- ↑ information entropy
- ↑ Iterative Dichotomiser 3
- ↑ recursion
- ↑ Classification and Regression Trees,意思係分類與迴歸樹噉解。
- ↑ Gini Index,留意呢個字詞同經濟學上講嘅堅尼系數(一種用嚟量度貧富差距嘅指標)係兩樣唔同嘅嘢。
- ↑ overfitting
- ↑ pruning
- ↑ pre-pruning
- ↑ post-pruning
- ↑ random forest
- ↑ boosted regression tree
- ↑ 1.0 1.1 Cameron Browne; Edward Powley; Daniel Whitehouse; Simon Lucas; Peter I. Cowling; Philipp Rohlfshagen; Stephen Tavener; Diego Perez; Spyridon Samothrakis; Simon Colton (March 2012). "A Survey of Monte Carlo Tree Search Methods". IEEE Transactions on Computational Intelligence and AI in Games. 4 (1): 1–43.
- ↑ Sharma, H., & Kumar, S. (2016). A survey on decision tree algorithms of classification in data mining. International Journal of Science and Research (IJSR), 5(4), 2094-2097,佢亦有提到一啲用嚟做決策樹分析嘅軟件。
- ↑ Demystifying Entropy. Towards Data Science.
- ↑ Fazlollah M. Reza (1994) [1961]. An Introduction to Information Theory. Dover Publications, Inc., New York.
- ↑ Gray, R. M. (2011), Entropy and Information Theory, Springer.
- ↑ 6.0 6.1 6.2 Hssina, B., Merbouha, A., Ezzikouri, H., & Erritali, M. (2014). A comparative study of decision tree ID3 and C4.5 (PDF). International Journal of Advanced Computer Science and Applications, 4(2), 13-19,有講解 C4.5 點樣運用 Gain Ratio 嚟取代資訊熵。
- ↑ Decision Trees: ID3 Algorithm Explained. Towards Data Science.
- ↑ Azar, A. T., & El-Metwally, S. M. (2013). Decision tree classifiers for automated medical diagnosis. Neural Computing and Applications, 23, 2387-2403.
- ↑ CART (Classification And Regression Tree) in Machine Learning. GeeksForGeeks. "It works on categorical variables, provides outcomes either 'successful' or 'failure' and hence conducts binary splitting only."
- ↑ Bramer, M. (2007). Avoiding overfitting of decision trees. Principles of data mining, 119-134.
- ↑ Pruning decision trees. GeeksForGeeks.
- ↑ Modeling - Basic Tree With Default Parameters. Learn by Marketing.
- ↑ Scornet, Erwan (2015). "Random forests and kernel methods". arXiv:1502.03836
- ↑ Gradient Boosting vs Random Forest. GeeksForGeeks.
外拎
[編輯]- (英文) 乜嘢係決策樹?,呢篇文簡介點樣响機械學習上使用決策樹。
- (英文) SPSS 決策樹可以為你盤生意作出咩貢獻
- (英文) 用 R 程式語言嚟行決策樹學習,Guru99
- (英文) C4.5 演算法係乜,佢係點運作嘅? Towards Data Science

















