電子遊戲嘅人工智能
電子遊戲嘅人工智能,顧名思義,係指電子遊戲當中嘅人工智能(AI):電子遊戲係一種電腦程式,曉同玩家互動,以娛樂玩家為目的;電子遊戲好多時會用到由電腦控制,同玩家對局嘅角色(NPC)[1],而開發者為咗想玩家玩得開心過癮,往往會希望由電腦控制嘅角色有返咁上下聰明,能夠為玩家提供一定嘅挑戰[2];噉即係話佢哋會想 NPC 展現一定程度嘅智能,而 AI 呢個領域正正就係想教電腦程式做出有智能行為嘅[3][4]。
舉個簡單例子,《食鬼》(1980 年)呢隻經典遊戲係遊戲 AI 嘅早期例子,隻遊戲入便嘅敵人(鬼)由電腦控制,會追捕由玩家控制嘅主角,喺正常情況下主角一畀啲鬼掂到就會死。要教啲鬼追捕玩家,可以用類似以下噉嘅演算法[5]:
Pac-Man.pos // 遊戲程式知道主角喺邊個位置。
clyde_target = random_tiles // 將 clyde_target 設做是但隨機一格。
while game == in_play: // 喺隻遊戲進行途中嘅每一點時間,
case player of:
Blinky: move 1 tile toward Pac-Man.pos
// 第一隻鬼 Blinky 要向主角嘅位置(Pac-Man.pos)行一步。
Inky: move 1 tile toward (Pac-Man.pos + 4)
// 第二隻鬼 Inky 要向主角位置前四格行一步。
Clyde: if Clyde.pos == clyde_target:
clyde_target = (clyde_target + 1) % 10
else:
move 1 tile toward clyde_target
// Clyde 呢隻鬼要向佢嘅目標位置前進,如果到咗目標位置,揀個新嘅目標位置。
上述嘅演算法會令啲鬼識得追趕主角——彷彿好似啲鬼展現緊智能噉[6]。
早期(講緊廿世紀中)嘅電子遊戲經已有用到簡單嘅 AI,而到咗廿一世紀初,遊戲 AI 仲成為咗遊戲製作上嘅一個大課題。遊戲製作專家會研究用咩演算法整一隻遊戲嘅 AI,先最可以為玩家帶嚟樂趣,而且 AI 仲有畀人用嚟做「控制 NPC」以外嘅工作,例如係做遊戲測試(隻遊戲出街前測試隻遊戲)以及對局配對(喺網上 PvP 遊戲當中,搵若干位玩家,將佢哋擺喺一個對局)... 等嘅工作,都會用到 AI 技術[7][8]。
一般嚟講,啲人想學遊戲 AI 通常會去學咗遊戲編程先。
基本模型
[編輯]啲人話要整遊戲 AI,主要涉及咗以下呢幾範:
- 移動:教 AI 控制(例如)一隻遊戲入便啲 NPC 敵人要點樣郁動。
- 決策:例如一隻潛行遊戲入便嘅 NPC 敵人決定「要繼續巡邏,抑或係要攻擊玩家?」——喺原始啲嘅電子遊戲入便,決策嘅方式可以幾簡單,例如想像個程式教個 NPC 做噉嘅簡單決策:「留意住自己離玩家幾遠,如果同玩家嘅距離短過 x,就進入攻擊模式,否則繼續巡邏」。亦可以睇吓捷思法嘅概念。
- 策略
- 支援 AI 嘅架構:例如要控制 AI 角色移動,遊戲程式好多時都要有一定嘅遊戲物理架構。
- 個體化定中央化:有啲遊戲會唔用個體化嘅 AI,即係唔會畀每個 NPC 自己做決定,而係由一個中央化嘅系統一嘢控制晒成個遊戲入便咁多位 NPC,例如《GTA III》對交通同行人嘅模擬就被指用咗呢種中央化嘅系統[9]。可以睇睇個體為本模型。
遊戲 AI 要用到各種嘅演算法同埋數據結構。同一般嘅 AI 製作唔同嘅係,遊戲 AI 一般都冇咁在意整出嚟嘅程式「係咪展現到好似人噉嘅智能」[10] ——原則上,AI 成個領域嘅目標係想整出有智能嘅物體,會用圖靈測試等嘅技術嚴格噉測試「呢個 AI 係咪真係展現到人類水平智能」,而遊戲 AI 就比較重視玩家係咪玩得開心過癮,比較肯接受「產生到假象,玩家以為佢哋有智能」嘅做法。
移動方法
[編輯]教 AI 移動嘅演算法係遊戲 AI 嘅基礎之一:除非係好似互動式小說等嘅類型,絕大多數嘅電子遊戲都會有一笪虛擬空間,畀遊戲角色喺裡便郁動;好似《食鬼》等嘅早期電子遊戲經已有喺度用演算法教 NPC 探索遊戲空間,而呢個時期用嘅演算法有啲到咗廿一世紀都仲有人用[5]。喺比較簡單嘅情況下,一個電子遊戲 AI 嘅移動演算法會攞遊戲空間入面其他物件嘅運動特性做輸入,並且用呢啲輸入計出個 AI 角色應該要移向邊個方向或者位置[註 1]:
- 輸入
input:第啲物件或者個 AI 角色本身嘅 - 輸出
output:個 AI 角色跟住落嚟嘅
舉個簡單例子,好似係一個教 NPC 避子彈嘅演算法,就通常要有方法俾個 AI 角色知道子彈嘅位置、方向同速度,再計出個 AI 角色應該向自己施一股點嘅力,或者有個點嘅加速度,先可以避開粒子彈[11]。
- 例子碼 1
喺遊戲 AI 上,其中一樣最基本嘅嘢係教 AI 追敵人,例如遊戲敵人追蹤玩家,嘗試接近同攻擊玩家角色。以下係教一個 AI 追蹤(seek)一件物件嘅演算法[12]:
class KinematicSeek:
// Declare 個演算法控制緊邊個角色同要追嘅目標
character, target
// Declare 個角色嘅最大速度
maxSpeed
def getSteering():
// 整個 output 嘅結構
steering = new KinematicSteeringOutput()
// 攞個 steering 嘅方向
steering.velocity = target.position - character.position // 如果將呢個數變成隨機,可以用嚟教個 AI 隨機行嚟行去(wandering)。
if steering.velocity.length() < radius: // 如果同目標之間嘅距離細過某個特定數值,就唔使郁。
return none
// 計出個 exact 嘅速度
steering.velocity.normalize()
steering.velocity *= maxSpeed
// 轉向要郁嘅方向
character.orientation = getNewOrientation(character.orientation,steering.velocity)
// 將個 steering 俾做 output
steering.rotation = 0
return steering
順帶一提,將 target.position - character.position 改做 character.position - target.position 就可以令段演算法變成教個 AI 避開一件物件[12]。再進一步嘅演算法仲會教埋個 AI 離目標有返咁上下近就要剎掣、將方向對準、以及將自己嘅速度變成同目標一致等等嘅功能[13]。
- 例子碼 2
以下呢段碼定義咗兩個子程式用嚟教人工智能避開障礙物[14]:
private function collisionAvoidance() :Vector3D { // 計要點樣避,呢個子程式俾嘅結果會係一股力(睇返上面遊戲物理嗰度)。
ahead = ...; // calculate the ahead vector
ahead2 = ...; // calculate the ahead2 vector
var mostThreatening :Obstacle = findMostThreateningObstacle(); // 用「findMostThreateningObstacle」呢個子程式搵出最有威脅性嘅障礙物。
var avoidance :Vector3D = new Vector3D(0, 0, 0);
if (mostThreatening != null) { // 如果有障礙物,計避開嗰股力要係幾多,用「最有威脅性嘅障礙物」嘅位置同個角色嘅速度計。
avoidance.x = ahead.x - mostThreatening.center.x;
avoidance.y = ahead.y - mostThreatening.center.y;
avoidance.normalize();
avoidance.scaleBy(MAX_AVOID_FORCE);
} else {
avoidance.scaleBy(0); // nullify the avoidance force // 如果冇,避開嗰股力變 0(唔使避)。
}
return avoidance;
}
private function findMostThreateningObstacle() :Obstacle { // 用嚟搵出環境入面邊件障礙物最危險嘅子程式
var mostThreatening :Obstacle = null; // 首先將「最有威脅性嘅障礙物」設做「冇嘢」。
for (var i:int = 0; i < Game.instance.obstacles.length; i++) { // 逐件逐件障礙物計一次
var obstacle :Obstacle = Game.instance.obstacles[i];
var collision :Boolean = lineIntersecsCircle(ahead, ahead2, obstacle); // 計吓個角色會唔會同件障礙物相撞
// "position" 係個角色現時嘅位置
if (collision && (mostThreatening == null || distance(position, obstacle) < distance(position, mostThreatening))) {
// 如果會相撞,而且件障礙物近過目前手上最近嗰件「最有威脅性嘅障礙物」嘅話,將件障礙物設做「最有威脅性嘅障礙物」。
mostThreatening = obstacle;
}
}
return mostThreatening; // 將最後「最有威脅性嘅障礙物」俾做輸出。
}
喺個遊戲程式「更新遊戲狀態」嘅部份入面會有「foreach 人工智能角色,幫佢做 collisionAvoidance()」噉嘅碼[14]。
搵路
[編輯]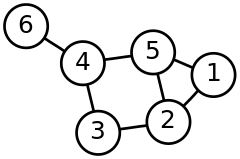
搵路(pathfinding / pathing)係人工智能上嘅一個大課題,指教一個 AI 喺空間入面指定兩個點,並且搵出一條連接兩點嘅線。做搵路嘅演算法有好多用途,例如喺機械人學上教機械人探索自己周圍嘅空間,以及喺遊戲製作上教遊戲 AI 喺遊戲空間入面搵出要行嘅路線[15][16]。
一般嚟講,搵路演算法-無論係咪電子遊戲用嘅都好-都會[17][18]
- 攞一幅圖做輸入
input:呢類演算法通常唔能夠直接處理一個環境,而係要靠第個演算法,simplify,將個環境變成一幅圖(graph);圖論當中嘅一幅圖會有若干個節點(node),並且指明邊啲節點之間有連結,喺應用上,一個可能嘅做法係個輸入最先嗰個數字代表節點嘅數量,跟住嘅數字表示邊啲節點之間有連結(睇埋陣列),例如[6, 1-2, 1-5, 2-5, 2-3, 5-4, 3-4, 4-6]表示幅圖有 6 個節點,節點 1 同節點 2 之間有連結(可以由節點 1 行去節點 2 或者相反)、節點 1 同節點 5 之間有連結(可以由節點 1 行去節點 5 或者相反)... 如此類推;simplify要做嘅嘢係攞要探索嗰個環境做輸入,輸出一個表示個環境當中有邊啲重要位置(節點)同邊啲位置之間有路能夠互通(連結)嘅圖,等搵路演算法做嘅嘢容易啲[17]。 - 喺電子遊戲入面用嘅搵路演算法通常會用權重表(weighted graph),意思即係話個表每條連結都會有個數值[註 2],表示嗰條路線嘅成本(cost)[19]:例如有一個
simplify演算法會每條路都俾個權重值佢,個數值愈大表示條路愈難行(成本高);想像其中兩個節點之間有兩條可能路線a同b,a係一條完全冇機關嘅平路,而b長過a之餘仲有十個陷阱設咗喺度,噉正路嚟講,假設a同b喺其他因素上完全相等,b嘅權重值理應會大過a嘅[20]。 - 最後個演算法會俾一條路線嚟做輸出
output[21]。
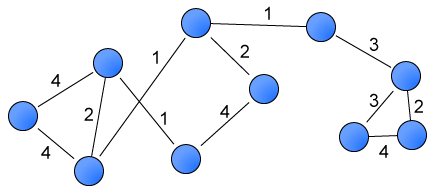
一個搵路演算法嘅輸入 input 望落大致上係噉嘅[17]:
class Graph:
// 搵出柞連結
def getConnections(fromNode)
class Connection: // 每條連結...
// 條連結有個非負嘅數做佢權重
def getCost()
// 條連結由邊個節點出發
def getFromNode()
// 條連結去邊個節點
def getToNode()
有關搵路嘅具體演算法,可以睇吓迪卡斯特拉演算法同埋會用某啲捷思法考慮預計成本嘅 A* 搜尋演算法[17][22][23]。
決策
[編輯]決策係指「由一柞可能選擇當中揀一個」嘅過程。廿世紀嘅電子遊戲 AI 幾乎冚唪唥都會用基於規則嘅系統(rule-based system)[24],例如想像一個寫嚟教電腦玩射擊遊戲嘅 AI,個 AI 係一部有限狀態機(finite-state machine),有「防守」、「進攻」同「去搵彈藥」等多個可能狀態,佢內置嘅 AI 演算法就要教佢幾時進入邊個狀態(例:if 自己淨低嘅生命值低過 50%,then 進入防守狀態-教佢喺自己血低嗰陣要防守)。呢類決策演算法會攞同遊戲輸贏相關嘅資訊(自己同對手血量等等),並且計出要進入邊個狀態(採取邊個策略)。有限狀態機同搵路呢兩個概念係遊戲 AI 嘅基礎[25][26]。
一個以有限狀態機形式存在嘅遊戲 AI 望落會有類似噉嘅碼[27][28]:
void Update(){ // 呢段碼教一個 AI 玩揸戰機。
switch(state){ // 視乎 state(狀態)係乜,做...
case State.PURSUIT: // 如果狀態係 pursuit(追擊)嘅話,做...
CheckForDanger(); // 一個睇吓周圍有冇危險嘅子程序
Chase(target, true); // 追目標;呢個子程序當中會有演算法,決定幾時要將 state 呢個變數改變並且離開個子程序。
break;
case State.DARWINISM: // 如果狀態係 Darwinism 嘅話,做...
var angle = GetDeltaAngle(target); // ... 同一道理
SteerClear(angle);
if(!IsOnCollisionCourse) state = pausedState;
break;
case State.FOLLOW: // ...
CheckForDanger();
Chase(squadron.leader);
EvaluateSquadron();
break;
case State.PATROL: // ...
CheckForDanger();
FlyTo(route.goingTo);
PatrolManagement(20);
break;
}
void Chase(target, true){ // Chase 呢個子程序
... // 做 chase 狀態要做嘅行動。
if (.....) // 如果某啲條件達到...
break; // 離開子程序,令個程式返到去揀狀態嘅點。
}
快思邏輯
[編輯]快思邏輯(fuzzy logic)係相對於一係「真」一係「假」嘅布林邏輯嘅一種邏輯。想像家陣有杯水,研究者想按杯水嘅攝氏溫度將杯水分落「熱」、「暖」同「凍」三個類別,佢可以用布林邏輯嚟分-15 度以下嘅係凍、15 至 40 度嘅係暖... 如此類推,即係話「杯水屬熱」呢句陳述式只能夠係真(1)或者假(0);另一方面,佢可以用快思邏輯嚟分-10 度以下嘅實係凍,而 10 至 20 度之間嘅水會介乎於凍同暖之間,例如一杯 15 度嘅水會係 0.5 凍 0.5 暖... 如此類推,「杯水屬熱」呢句陳述式嘅數值可以喺真(1)同假(0)之間。快思邏輯呢種思考法係喺 1960 年代中興起嘅[29]。
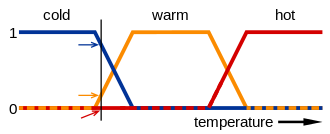
快思邏輯喺電子遊戲上都會有用:想像一隻射擊遊戲當中曉同玩家角色戰鬥嘅 AI 角色;佢具有生命值呢個屬性,而且係一部有限狀態機-喺每個時間點,佢有「去搵藥包回復生命值」同「繼續戰鬥」呢兩個可能狀態,
- 如果個程式用嘅係布林邏輯,佢可能會按「
if 生命值 < 50%, then 去搵藥包回復生命值, else 繼續戰鬥」嘅邏輯行事, - 另一方面,佢又可以用快思邏輯行事,例:
if 生命值 < 20%, then 去搵藥包, else if 20% <= 生命值 < 40%, then 一路繼續戰鬥一路同藥包位置維持 x 咁多嘅距離,當中 x = f(淨低嘅生命值),即係一個介乎於「繼續戰鬥」同「去搵藥包」之間嘅狀態。 ...
喺多數情況下,用快思邏輯製作遊戲 AI 會令個 AI 變得更加似人-人類做起決策上嚟都係一定程度跟快思邏輯嘅[28][30]。
決策樹
[編輯]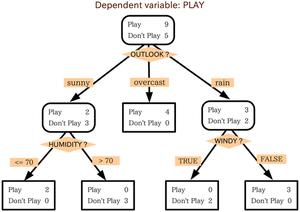
決策樹(decision tree)係一種用樹狀圖做決策嘅做法。一樖決策樹會有若干個節點(node),每個節點代表一個決策點,會有若干個箭咀指去下一柞節點(下一步),每個箭咀表示「如果揀咗呢個選項,就去呢個決策點」。想像附圖嗰樖決策樹,
- 個決策者想決定好唔好去玩,
- 喺開頭個節點,去玩(play)嘅價值有 9 分,唔好去玩(don't play)嘅價值有 5 分,然後睇天氣(OUTLOOK),
- 如果晴天(sunny),去玩嘅價值變成 2 分,唔好去玩嘅價值變成 3 分,然後個決策者會睇濕度(HUMIDITY)... 如此類推。
喺運算上,一樖決策樹節點數量 愈大,運算樖樹要用嘅時間就愈多[31][32]。
喺遊戲 AI 上,蒙地卡羅樹搜索(Monte Carlo tree search,MCTS)係一種比較實際嘅做法:現實世界嘅電子遊戲嘅決策樹通常都大得好交關,可能去到第二第三步經已有成幾千個節點,夾硬考慮嗮所有嘅可能性喺實際應用上根本唔可行;MCTS 簡單啲講就係有技巧噉搜索一樖決策樹-會揀定一個深度值 做「要考慮幾多步」,並且喺每步按某啲準則揀邊啲節點嘅下一步值得考慮(例如可能搵個人工神經網絡計吓邊啲節點比較有可能發生),而如果上述嘅演算法設計得夠好,MCTS 可以有效噉教電腦玩遊戲[33][34]。2016 年打贏九段圍棋棋手李世石而出名嘅人工智能程式 AlphaGo 就係用咗 MCTS 嘅技術[35]。
struct RandomDecision (Decision):
lastFrame = -1
lastDecision = false
def test():
if frame() > lastFrame + 1:
lastDecision = randomBoolean()
lastFrame = frame()
return lastDecision
策略戰術
[編輯]一個遊戲 AI 唔淨只要識得做決策,而且仲有識得判斷邊個選擇能夠令佢打贏嘅機會率最大化。一般嚟講,一個遊戲 AI 需要有一套策略(strategy),套策略會講明「喺情況 我會採取噉嘅行動」、「喺情況 我會採取噉嘅行動」... 等等嘅資訊,令佢喺適當嘅時候用適當嘅戰術(tactics);策略喺遊戲 AI 上係一個重大課題-聰明嘅 AI 能夠令一隻遊戲更加好玩,而且理論性啲嘅人工智能研究亦都對「點樣令一部電腦出現有智能嘅策略性行動」呢個問題感興趣[24][36]。
喺有地圖嘅遊戲類型當中,遊戲 AI 演算法好多時會運用對地圖唔同位置嘅戰略價值嘅判斷:例如想像一隻射擊遊戲,設計者想教遊戲 AI 有策略噉喺地圖上移動同揀企嘅位置,佢可以用演算法將地圖變成一幅圖論入面嘅圖(睇返上面搵路),然後按照一套事先制訂咗嘅演算法 judge value,judge value 會每個節點都俾個數值 佢, 代表咗嗰個位置喺戰術上有幾有利( 會取決於嗰個位置嘅高度、掩護物嘅存在、有冇逃走路線以及有冇彈藥供應等嘅因素),並且喺每個時間點一路決定自己應該要喺邊個狀態(睇返上面有限狀態機嘅嘢)一路嘗試盡量將自己移向 值高嘅位置[註 4];當中 judge value 嘅質素-有幾能夠準確噉判斷一個位置嘅戰略價值-反映個 AI 嘅戰略能力。呢種做法喺現實嘅軍事策略入面都會用到。事實係,喺動作遊戲同戰略遊戲嘅 AI 設計當中,設計師往往會參考現實世界嘅軍事策略[36]。
協調行動
[編輯]喺廿一世紀嘅電子遊戲當中,一個 AI 角色好多時唔淨只要單獨噉行動,仲要識得同(由 AI 或者玩家控制嘅)第啲個體合作:喺好多戰略遊戲同動作遊戲入面都會有成隊人一齊上嘅 AI 敵人角色,又有啲戰略射擊遊戲會俾玩家扮演指揮官,一路戰鬥一路指揮住由 AI 控制嘅隊友,例:隊友係有限狀態機,有「掩護玩家」、「去搵彈藥」同「進攻」等多個狀態,玩家可以指定佢哋要去邊個狀態[註 5]。喺呢啲情況下,一個噉嘅 AI 角色內部嘅演算法要攞「同佢合作緊嗰啲個體嘅行動」作為 input;呢類 AI 大致上可以按「會唔會由高層嗰度收 input」分做兩類-
- 由上至下(top-down),指某個高層個體會攞一啲
input,並且對下層嘅個體落命令,好似現實世界由將軍等高階將士指揮軍隊作戰噉;呢啲高層個體好多時能夠鳥瞰遊戲地圖,所以佢哋手上會有一啲下層個體冇嘅資訊;同埋 - 由下至上(bottom-up),指各個個體分別噉對自己周圍嘅環境嘅變數(包括視線範圍內嘅隊友)作出判斷,並且
output各自嘅行動,而唔會由任何高層嗰度收命令;喺某啲情況下,呢類演算法可以引致望落好似成個隊伍有一個智能噉嘅行為(可以睇埋群體智能)[36][37]。
呢兩種做法各有優劣。
學習
[編輯]機械學習(machine learning,簡稱 ML)係人工智能上嘅一種技術。指用程式編寫教一部電腦做學習,典型做法如下[38][39]:p. 2:
- 編寫一個程式,教部電腦點樣由數據嗰度建立一個數學模型嚟描述佢對啲變數之間嘅關係嘅知識;
- 搵啲樣本數據(即係所謂嘅「訓練數據」)返嚟,俾個程式處理吓啲數據入面嘅個案,等部電腦按個程式建立一個數學模型;跟住
- 喺將來再撞到同類個案嗰時,部電腦就會曉按佢個程式,用建立咗嗰個模型,對呢啲之前未見過嘅個案作出預測-個設計者唔使明文噉教部電腦點樣應對呢啲前所未見嘅個案,部電腦都會有能力一定程度上應對。
原則上,如果一個遊戲 AI 能夠記住玩家過去嘅行為(描述玩家行為嘅變數數值就係數據),再按呢樣資訊改變自己嘅行為,噉就會做到「遊戲 AI 曉學習同適應,持續為玩家提供新挑戰」嘅效果。一個簡單嘅例子有以下噉嘅做法[40]:
記低玩家而家選擇咗邊個戰術, 按手上數據(玩家喺過去 n 個時間點每一個當中揀咗邊個戰術),計算玩家揀每個戰術嘅機會率, 將出現機會率最大嘅戰術做「預佢會用嘅戰術」。 揀選能夠最有效噉應對「預佢會用嘅戰術」嘅戰術。
廿一世紀初嘅遊戲 AI 界變得重視對機械學習嘅討論:一方面,有好多遊戲設計師都希望自己嘅遊戲嘅 AI 可以做到曉學習,不過另一方面又有遊戲設計學者指出,曉學習嘅遊戲程式有「難控制難預測」嘅問題,而遊戲環境太難預測好多時會搞到玩家冇癮[41][42]。亦有 AI 領域嘅科學家指出,電子遊戲本質上就係設計嚟俾一個認知系統慢慢學習(遊戲難度一般會慢慢提高)嘅,所以電子遊戲係一個好便於研究點樣教 AI 學習嘅環境-遊戲製作同 AI 呢兩個領域做到相輔相成[43][44]。
喺現實世界嘅遊戲製作當中,機械學習嘅遊戲 AI 通常係離線(offline)做嘅:想像有個網上遊戲程式,會一路俾玩家玩一路學習,所以會係噉變化,但噉通常會引致一個問題-喺管理網上遊戲嘅途中,製作組要做程式除錯(debugging)嘅工作,而要檢查程式錯誤,個錯誤就一定要能夠重複出現,等編程員慢慢研究個錯誤係點嚟,所以俾個遊戲程式係噉變化會搞到除錯嘅工作變得撈絞。因為呢個緣故,遊戲 AI 機械學習(尤其係網上遊戲)比較常用嘅做法係離線做,即係例如每隔一段時間就要個網上遊戲程式離線,按機械學習演算法更新,先至再上返線[40]。
第啲應用
[編輯]
喺廿世紀嗰陣,遊戲 AI 嘅用途幾乎完全局限於教遊戲程式點樣控制啲 NPC,搵路、有限狀態機同蒙地卡羅樹搜索等嘅技術都係噉。但自從廿一世紀開始,遊戲 AI 界開始將人工智能嘅相關技術應用落去其他嘅用途嗰度,包括[3]:
- 玩家體驗模擬(player experience modeling):遊戲製作其中一個最重要嘅目的係要令玩家玩嗰陣開心過癮;人工智能相關技術可以用嚟建立模擬玩家體驗嘅模型,呢啲模型一般會攞描述遊戲參數嘅變數做
input(例如係關卡嘅參數(有幾多敵人、幾長...)同遊戲畫面呀噉),而output就係(個模型所預測嘅)玩家體驗,後者可以用「喺玩家玩完之後,問佢哋 1 至 10 分會俾隻遊戲幾多分」等嘅方法量度;然後研究者可以用監督式學習訓練人工神經網絡由遊戲參數預測玩家體驗-如果順利嘅話,個模型可以話到俾製作組聽,「如果隻遊戲係噉噉噉樣,玩家嘅體驗會係噉噉噉樣」等嘅資訊[45][46]。可以睇埋用嚟做偏好學習(preference learning)嘅人工神經網絡[47][48]。 - 程序生成(procedural generation):程序生成係電腦科學上嘅概念,指用演算法嚟生成數據嘅做法。舉個例子說明,程序生成喺電子遊戲設計上好常用:有啲遊戲可能會想幅地圖嘅地形有啲隨機性嘅起伏-例子有做個創世神(Minecraft)-於是個遊戲程式要嘅嘢就唔係好似一般嘅遊戲噉,死記住幅地圖係乜嘢樣嘅,而係記住一段演算法,並且喺個玩家要求個程式整一幅地圖(撳「開始遊戲」)嗰時,即場用段演算法整一幅地圖出嚟。呢啲演算法當中可以有隨機性,所以次次產生地圖嗰陣,最後出嗰幅地圖都唔同樣[49][50]。而家想像一個遊戲程式,要用程序生成整一個關卡出嚟俾玩家玩,佢可以用類似噉嘅做法嚟將玩家滿足感最大化[51][52]:
- 用程序生成,產生 n 個關卡;
- Foreach 產生出嚟嘅關卡,
- 用一個事先訓練好嘅人工神經網絡(睇返上面玩家體驗模擬),預計呢個關卡會造成幾高嘅玩家滿足感;
- 揀預計玩家滿足感最高嗰個關卡俾玩家玩。
- 遊戲分析(game analytics):遊戲分析係行為分析(behavioral analytics)嘅一種,指遊戲製作者特登將遊戲程式編寫成曉紀錄玩家行為嘅相關數據,並且按呢啲數據做有關管理隻遊戲嘅決策;舉個例說明,一隻網上遊戲,製作者將個遊戲程式編寫成曉紀錄遊戲世界入面每個地點有幾多玩家到訪同每個玩家喺嗰度逗留幾耐,而佢哋發現有個地點零舍唔受歡迎(好少玩家到訪,玩家平均逗留時間短),於是就更改嗰個地點嘅設計,等嗰個地點有趣啲,打後嘅數據反映玩家到訪次數多咗同逗留時間長咗[53][54]。有唔少人工智能相關嘅技術都可以攞嚟幫手做遊戲分析方面嘅工作,例如聚類分析(cluster analysis;一種按若干個變數將個案分做聚類嘅分析方法)就試過俾人攞嚟將一隻遊戲嘅玩家按「玩遊戲嗰陣嘅行為」嚟分類[55]。
- 電子遊戲機械人(video game bot):係一啲特殊嘅人工智能程式,曉一定程度上代人打機;用家要用某啲方法將隻遊戲嘅狀態做
input俾個機械人,然後個程式又要曉用某啲方法做運算,再俾出一個output,output代表佢決定要撳嘅掣,靠噉嚟俾個機械人玩隻遊戲。寫得夠好嘅機械人表現仲可以超越人類玩家,有啲玩家會用機械人嚟出茅招-聲稱佢係靠自己玩,但查實係用機械人代佢玩嘅;另一方面,喺遊戲製作過程當中,遊戲製作者有陣時亦會用機械人嚟測試隻遊戲[56][57]。
演算法
[編輯]睇埋
[編輯]文獻
[編輯]- Bourg; Seemann (2004). AI for Game Developers. O'Reilly & Associates. ISBN 0-596-00555-5.
- Buckland (2002). AI Techniques for Game Programming. Muska & Lipman. ISBN 1-931841-08-X.
- Buckland (2004). Programming Game AI By Example. Wordware Publishing. ISBN 1-55622-078-2.
- Champandard (2003). AI Game Development. New Riders. ISBN 1-59273-004-3.
- Cruz, C. A., & Uresti, J. A. R. (2017). Player-centered game AI from a flow perspective: Towards a better understanding of past trends and future directions (PDF). Entertainment Computing, 20, 11-24.
- Funge (1999). AI for Animation and Games: A Cognitive Modeling Approach. A K Peters. ISBN 1-56881-103-9.
- Funge (2004). Artificial Intelligence for Computer Games: An Introduction. A K Peters. ISBN 1-56881-208-6.
- Le Hy, R., Arrigoni, A., Bessiere, P., & Lebeltel, O. (2004). Teaching bayesian behaviours to video game characters (PDF). Robotics and Autonomous Systems, 47(2-3), 177-185.
- Millington (2005). Artificial Intelligence for Games. Morgan Kaufmann. ISBN 0-12-497782-0.
- Schaeffer, J. (2001). A gamut of games. AI Magazine, 22(3), 29-29.
- Schwab (2004). AI Game Engine Programming. Charles River Media. ISBN 1-58450-344-0.
- Smed and Hakonen (2006). Algorithms and Networking for Computer Games. John Wiley & Sons. ISBN 0-470-01812-7.
- Spronck, P., Sprinkhuizen-Kuyper, I., & Postma, E. (2004, November). Difficulty scaling of game AI. In Proceedings of the 5th International Conference on Intelligent Games and Simulation (GAME-on 2004) (pp. 33-37).
- Thompson, T. (2019). Why Friendly AI Cheat in Ghost Recon Wildlands. Gamasutra.
- Yannakakis, G. N. (2012). "Game AI revisited" (PDF). Proceedings of the 9th Conference on Computing Frontiers: 285–292.
- Woodcock, S. (1999). Game AI: The State of the Industry. Gamasutra.
- Zook, A., & Riedl, M. (2012, October). A temporal data-driven player model for dynamic difficulty adjustment. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment (Vol. 8, No. 1).
註釋
[編輯]- ↑ 有關呢啲概念喺物理上可以點樣分析,可以睇吓古典力學同剛體動力學。而有關呢啲嘢數學上點分析,可以睇睇向量同矩陣嘅概念。
- ↑ 喺實際應用上,呢啲數值通常一定係 0 或者正數,因為好多常用嘅搵路演算法一撞到負數嘅權重值就會出錯。
- ↑ 有啲演算法仲會精細到考慮埋連結之間嘅方向性:即係有啲路可能淨係可以向其中一個方向通行,又或者由一個方向行嘅成本同由第個方向行嘅唔同。
- ↑ 個 AI 嘅狀態可能會影響一個位置嘅 值。例:如果一個 AI 生命值低,進入咗「搵地方匿埋同回復生命值」嘅狀態,佢理應會想去便於防守嘅位置多過想去便於攻擊嘅位置。
- ↑ 順帶一提,現實嘅遊戲通常都係玩家指揮 AI 而唔係 AI 指揮玩家,因為主流遊戲設計師認為俾玩家做指揮,隻遊戲會好玩啲。
引咗
[編輯]- ↑ "The Next Generation 1996 Lexicon A to Z: NPC (Nonplayer Character)". Next Generation. No. 15. Imagine Media. March 1996. p. 38.
- ↑ Yannakakis, G. N., & Hallam, J. (2007). Towards optimizing entertainment in computer games. Applied Artificial Intelligence, 21(10), 933-971.
- ↑ 3.0 3.1 Yannakakis, Geogios N (2012). "Game AI revisited" (PDF). Proceedings of the 9th Conference on Computing Frontiers: 285-292.
- ↑ Stanley, K. O., Bryant, B. D., & Miikkulainen, R. (2005). Evolving neural network agents in the NERO video game. Proceedings of the IEEE, 182-189.
- ↑ 5.0 5.1 Pac-Man 互聯網檔案館嘅歸檔,歸檔日期2021年2月11號,..
- ↑ Bogost, Ian (March 2017). ""Artificial Intelligence" Has Become Meaningless". Retrieved 22 July 2017.
- ↑ Lu, F., Yamamoto, K., Nomura, L. H., Mizuno, S., Lee, Y., & Thawonmas, R. (2013, October). Fighting game artificial intelligence competition platform. In 2013 IEEE 2nd Global Conference on Consumer Electronics (GCCE) (pp. 320-323). IEEE.
- ↑ Delalleau, O., Contal, E., Thibodeau-Laufer, E., Ferrari, R. C., Bengio, Y., & Zhang, F. (2012). Beyond skill rating: Advanced matchmaking in ghost recon online. IEEE Transactions on Computational Intelligence and AI in Games, 4(3), 167-177.
- ↑ DMA Design. Grand Theft Auto 3. Published by Rockstar Games, 2001. PlayStation 2.
- ↑ Millington, I. (2019). AI for Games. CRC Press. 2.2.1 有提到 "illusion of intelligence"。
- ↑ Millington, I. (2019). AI for Games. CRC Press. p. 42-48.
- ↑ 12.0 12.1 Millington, I. (2019). AI for Games. CRC Press. p. 52 - 53.
- ↑ Millington, I. (2019). AI for Games. CRC Press. p. 62 - 64.
- ↑ Cui, X., & Shi, H. (2011). A*-based pathfinding in modern computer games. International Journal of Computer Science and Network Security, 11(1), 125-130.
- ↑ Boyarski, E., Felner, A., Stern, R., Sharon, G., Tolpin, D., Betzalel, O., & Shimony, E. (2015, June). ICBS: improved conflict-based search algorithm for multi-agent pathfinding. In Twenty-Fourth International Joint Conference on Artificial Intelligence.
- ↑ 17.0 17.1 17.2 17.3 Millington, I. (2019). AI for Games. CRC Press. Ch. 4.
- ↑ Hagelback, Johan, and Stefan J. Johansson. "Dealing with fog of war in a real-time strategy game environment." In Computational Intelligence and Games, 2008. CIG'08. IEEE Symposium On, pp. 55-62. IEEE, 2008.
- ↑ Fletcher, Peter; Hoyle, Hughes; Patty, C. Wayne (1991). Foundations of Discrete Mathematics (International student ed.). Boston: PWS-KENT Pub. Co. p. 463. ISBN 978-0-53492-373-0. "A weighted graph is a graph in which a number w(e), called its weight, is assigned to each edge e."
- ↑ Antsfeld, L., Harabor, D. D., Kilby, P., & Walsh, T. (2012, October). Transit routing on video game maps. In Eighth Artificial Intelligence and Interactive Digital Entertainment Conference.
- ↑ Goodwin, S. D., Menon, S., & Price, R. G. (2006). Pathfinding in open terrain. In Proceedings of International Academic Conference on the Future of Game Design and Technology.
- ↑ Barnouti, N. H., Al-Dabbagh, S. S. M., & Naser, M. A. S. (2016). Pathfinding in strategy games and maze solving using A* search algorithm. Journal of Computer and Communications, 4(11), 15.
- ↑ Abd Algfoor, Zeyad; Sunar, Mohd Shahrizal; Kolivand, Hoshang (2015). "A Comprehensive Study on Pathfinding Techniques for Robotics and Video Games". International Journal of Computer Games Technology. 2015: 1–11.
- ↑ 24.0 24.1 Game AI: The State of the Industry. Gamastura. p. 1.
- ↑ Orkin, J. (2006, March). Three states and a plan: the AI of FEAR. In Game Developers Conference (Vol. 2006, p. 4).
- ↑ Gillies, M. (2009). Learning finite-state machine controllers from motion capture data (PDF). IEEE transactions on computational intelligence and AI in games, 1(1), 63-72.
- ↑ Designing a simple game AI using Finite State Machines. Gamasutra.
- ↑ 28.0 28.1 28.2 Millington, I. (2019). AI for Games. CRC Press. Ch. 5.
- ↑ Zadeh, L. A. (1988). Fuzzy logic. Computer, 21(4), 83-93.
- ↑ Game AI: The State of the Industry. Gamastura. p. 2.
- ↑ Bontrager, P., Khalifa, A., Mendes, A., & Togelius, J. (2016, September). Matching games and algorithms for general video game playing. In Twelfth Artificial Intelligence and Interactive Digital Entertainment Conference.
- ↑ Kleinsmith, A., & Gillies, M. (2013). Customizing by doing for responsive video game characters. International Journal of Human-Computer Studies, 71(7-8), 775-784.
- ↑ Cameron Browne; Edward Powley; Daniel Whitehouse; Simon Lucas; Peter I. Cowling; Philipp Rohlfshagen; Stephen Tavener; Diego Perez; Spyridon Samothrakis; Simon Colton (March 2012). "A Survey of Monte Carlo Tree Search Methods". IEEE Transactions on Computational Intelligence and AI in Games. 4 (1): 1–43.
- ↑ Monte Carlo Tree Search. Towards Data Science.
- ↑ Liu, Michael (10 October 2017). "General Game-Playing With Monte Carlo Tree Search". Medium.
- ↑ 36.0 36.1 36.2 Millington, I. (2019). AI for Games. CRC Press. Ch. 6.
- ↑ Díaz, G., & Iglesias, A. (2017, July). Intelligent behavioral design of non-player characters in a FPS video game through PSO. In International Conference on Swarm Intelligence (pp. 246-254). Springer, Cham.
- ↑ The definition "without being explicitly programmed" is often attributed to Arthur Samuel, who coined the term "machine learning" in 1959, but the phrase is not found verbatim in this publication, and may be a paraphrase that appeared later. Confer "Paraphrasing Arthur Samuel (1959), the question is: How can computers learn to solve problems without being explicitly programmed?" in Koza, John R.; Bennett, Forrest H.; Andre, David; Keane, Martin A. (1996). Automated Design of Both the Topology and Sizing of Analog Electrical Circuits Using Genetic Programming. Artificial Intelligence in Design '96. Springer, Dordrecht. pp. 151–170.
- ↑ Bishop, C. M. (2006), Pattern Recognition and Machine Learning, Springer.
- ↑ 40.0 40.1 Millington, I. (2019). AI for Games. CRC Press. Ch. 7.
- ↑ HOW ARTIFICIAL INTELLIGENCE WILL REVOLUTIONIZE THE WAY VIDEO GAMES ARE DEVELOPED AND PLAYED. The Verge.
- ↑ Stanley, K. O., Bryant, B. D., & Miikkulainen, R. (2005). Real-time neuroevolution in the NERO video game. IEEE transactions on evolutionary computation, 9(6), 653-668.
- ↑ Video Games as a Perfect Playground for Artificial Intelligence. Towards Data Science.
- ↑ Artificial Intelligence in Video Games. Towards Data Science.
- ↑ Yannakakis, G. N., & Hallam, J. (2008). Entertainment modeling through physiology in physical play. International Journal of Human-Computer Studies, 66(10), 741-755.
- ↑ Yannakakis, G. N., Martínez, H. P., & Jhala, A. (2010). Towards affective camera control in games. User Modeling and User-Adapted Interaction, 20(4), 313-340.
- ↑ G. N. Yannakakis. Preference Learning for Affective Modeling. In Proceedings of the Int. Conf. on Affective Computing and Intelligent Interaction, pages 126–131, Amsterdam, The Netherlands, September 2009. IEEE.
- ↑ G. N. Yannakakis, M. Maragoudakis, and J. Hallam. Preference Learning for Cognitive Modeling: A Case Study on Entertainment Preferences. IEEE Systems, Man and Cybernetics; Part A: Systems and Humans, 39(6):1165–1175, November 2009.
- ↑ Shaker, Noor; Togelius, Julian; Nelson, Mark J. (2016). Procedural Content Generation in Games: A Textbook and an Overview of Current Research. Springer.
- ↑ Moss, Richard (January 1, 2016). "7 uses of procedural generation that all developers should study 互聯網檔案館嘅歸檔,歸檔日期2019年8月27號,.". Gamasutra.
- ↑ Togelius, J., De Nardi, R., & Lucas, S. M. (2007, April). Towards automatic personalised content creation for racing games. In 2007 IEEE Symposium on Computational Intelligence and Games (pp. 252-259). IEEE.
- ↑ A. Martin, A. Lim, S. Colton, and C. Browne. Evolving 3D buildings for the prototype video game subversion. Applications of Evolutionary Computation, pages 111–120, 2010
- ↑ El-Nasr, M. S., Drachen, A., & Canossa, A. (2016). Game analytics. Springer London Limited.
- ↑ Bauckhage, C., Drachen, A., & Sifa, R. (2014). Clustering game behavior data. IEEE Transactions on Computational Intelligence and AI in Games, 7(3), 266-278.
- ↑ Drachen, A., Canossa, A., & Yannakakis, G. N. (2009, September). Player modeling using self-organization in Tomb Raider: Underworld. In 2009 IEEE symposium on computational intelligence and games (pp. 1-8). IEEE.
- ↑ Kaminka, G. A., Veloso, M. M., Schaffer, S., Sollitto, C., Adobbati, R., Marshall, A. N., ... & Tejada, S. (2002). Gamebots: a flexible test bed for multiagent team research. Communications of the ACM, 45(1), 43-45.
- ↑ Villanes, A. (2013). Analytical approach for bot cheating detection in a massive multiplayer online racing game. North Carolina State University.
拎
[編輯]- (英文) AI 學識點樣玩《食鬼》,YouTube,講到《食鬼》原作入便嘅 AI,幾隻鬼嘅性格都唔同,提到有限狀態機同搵路嘅概念,仲有係啲鬼用嘅演算法啲參數會點樣隨住過咗嘅關數量上升而改變。
- Special Interest Group on Artificial Intelligence @IGDA.
- AI Game Programming Wisdom on aiwisdom.com.
- Georgios N. Yannakakis and Julian Togelius.
- Titanfall 2 will bring back Attrition mode. Polygon.








