訊號

一個集成電路上面有好多微型嘅電路，用微電流嚟互傳訊號。

天線係用咗各種嘅原理，收以電磁波形式傳送嘅訊號，喺天文學上都會用到。

訊號（英文：signal，粵拼：粵化口語音：sik1 nou4）係工程學上嘅常用概念。定義上，訊號係指任何一個可以傳達資訊嘅函數^[1]。訊號處理常見於同通訊相關嘅工程領域，尤其係電子工程，而電子訊號主要係用變化嘅電壓、電流或者電磁波嚟傳嘅^[2]^[3]。

舉個例，想像家陣有兩個人，阿明同阿珍；而家阿明要去遠行，佢希望有能力遠距離傳資訊俾阿珍，等佢有得向阿珍報告行蹤；於是佢哋兩個事先講定個方案，搭好晒電線，用電訊號嚟傳羅馬字母－阿明同阿珍講，佢想傳資訊嗰陣，會傳一連串上上落落（設上為 1 下為 0）嘅電壓，一行資訊有嘅電壓數量實會係 4 嘅倍數，而每 4 個電壓用嚟代表一個字母；然後佢仲講明，1111 代表 A，1110 代表 B，1100 代表 C... 如此類推；用數學化啲嘅方式表達即係^[4]：

{\text{   信   息   }}={\begin{cases}{\text{A}},&{\mbox{if }}{\text{sik1 nou4}}=1111\\{\text{B}},&{\mbox{if }}{\text{sik1 nou4}}=1110\\{\text{C}},&{\mbox{if }}{\text{sik1 nou4}}=1100\\...\end{cases}}

當阿明去咗好遠嘅地方，佢向阿珍傳咗一串上上落落嘅電壓嗰時，阿珍可以攞住個解讀方案，解讀返阿明傳嗰一串 0 同 1 係想講乜－每吓呢啲上上落落嘅電壓就係一個訊號。而事實係，呢種用電壓上落傳達資訊嘅做法，正正就係廿世紀電子工程嘅基礎。

廣義化啲講，任何能夠喺時空當中變化嘅物理量都可以攞嚟做訊號^[5]：諸如影像、聲以至電磁波等都可以攞嚟做訊號－只要傳訊號嘅人（觀察者）之間有返套共同嘅方案，講明邊款訊號代表咩資訊，嗰啲訊號就會傳得到資訊。喺廿一世紀嘅科技裏面，聲（例如日常講嘢）、電磁波（例如電視嘅天線）同埋電壓上落（例如電子架生）等嘅物理量，都有俾人攞嚟做訊號^[1]^[6]。

定義

定義上，訊號係指是但一個^[1]

可以傳達資訊嘅函數。

例如有兩位研究者喺度研究太陽光，

A 君攞住感應器去量度某束光嘅強度 I，佢哋駁好晒電線，而 A 君同 B 君講好，佢會傳一個訊號，個訊號會係一個電壓，而電壓嘅大細 V 會同佢探測到嗰束光嘅強度成以下關係^[7]^[8]：

V=\beta I

當中

\beta

係個事先講好嘅數值，即係話

V

同

I

成特定嘅函數，假設 A 君靠得住，B 君能夠由呢個函數同埋收到嘅訊號當中，得知想知嘅資訊。

又例如兩位昆蟲學研究者，喺度研究蜜蜂，

A 君攞住部相機去影蜜蜂竇入面嘅蜂后，睇吓隻蜂后係咪如常生蛋，如果係佢就會傳一個正電壓（+1 V）俾 B 君，如果唔係佢就會傳一個負電壓（-1 V），所以個訊號（V）同隻蜂后行為正唔正常（x，用 1 代表正常）成噉嘅分段函數關係：

V={\begin{cases}-1,&{\mbox{if }}x=0\\1,&{\mbox{if }}x=1\end{cases}}

B 君又係可以由函數同埋收到嗰個訊號當中，得知目標資訊。

訊號係數值，而數值已知同收訊號嘅人想知嗰個變數之間成某啲特定關係（函數）所以收訊號嘅人有得睇住個訊號，得知佢想知嗰個變數係咩樣^{[註 1]}。

廿一世紀初嘅電子工程，就係用呢種技術達到長距離通訊嘅：簡化講，想像通訊雙方之間有電線，或者有天線等方法收發電磁波；通訊雙方可以彼此傳送一段段嘅微電壓－大電壓（1）或者細電壓（0）；佢哋可以事先講明每串可能嘅 1-0 組合代表邊個羅馬字母或者數字－即係例如 1111 代表 A、1110 代表 B、1100 代表 C... 呀噉，就能夠達到長距離通訊嘅效果；實際應用嘅電子工程會有更複雜嘅技術嚟傳送唔同嘅訊號^[9]。

摩斯碼都係用咗類似噉嘅原理：

分類

訊號可以按好多準則嚟分門別類。

數碼定模擬

數碼訊號

數碼訊號（digital）由離散嘅物理量集構成，表示一連串離散數值：數碼訊號嘅一個可能數值（例如 0）同下一個可能數值（例如 1）之間實會有個最細嘅可能差距，冇話斬件到幾細都得，即係例如數值冇得係 0.5 ^[10]^[11]。

數碼訊號喺廿一世紀嘅數碼電腦同埋各種電子架生當中好常見：呢啲機械會傳一串串由有電（1）同冇電（0）組成嘅訊號（好似下圖）並且用呢一串串嘅數值表示資訊，簡單講就係唔同嘅 1-0 組成代表唔同嘅符號，當中符號包括咗羅馬字母同數字呀噉^{[註 2]}；另一方面，亦都有啲數碼訊號做法係有三個或者以上嘅可能數值嘅^[12]^[13]。

數碼訊號之所咁常見，係因為呢種訊號有好多好處。數碼訊號其中一個最大嘅好處就係冇咁易受雜音影響－喺現實世界，訊號喺傳送中途梗會或多或少受干擾，跟住會走樣：

如果個訊號係模擬訊號（睇下面），個訊號嘅準確度實會受影響；
相比之下，如果個訊號係數碼，系統嘅設計者可以（例如）事先設定好部收訊號用嘅機械，叫部機跟噉嘅規律行事：如果電壓值細過 $V_{t}$ ，就當個訊號係 0 ；如果電壓值大過 $V_{t}$ ，就當個訊號係 1 。然後假想傳訊號嗰一刻，個訊號嘅可能數值分別係 $V_{0}$ 同 $V_{1}$ ；理論上，如果 $|V_{t}-V_{0}|$ 同 $|V_{t}-V_{1}|$ 嘅數值夠大，就算接收到嘅訊號走咗樣，最後得到嘅資訊都唔受影響^[14]^[15]。

好似係下圖噉，下圖 Y 軸表示收到嗰吓訊號嘅電壓值。喺現實世界，訊號實會受到干擾，所以實際收到嘅訊號近乎冇可能會完全可靠。

數碼訊號可以由模擬訊號轉化而成：舉例說明，家陣有部機，佢喺每個時間點會收一個數值係連續嘅電壓作為輸入，而輸出就係一串二元嘅數碼訊號（數值一係 1 一係 0 ），每 16 個訊號係一個二進制數字，代表一個時間點嘅輸入電壓值，例如如果輸出係 0000 0001 0010 0010，就代表輸入電壓值係 290 V－290 喺二進制入面係 1 0010 0010 。事實上，呢種做法喺現代電子工程當中極之常見，例如遊戲機嘅遊戲搖桿都用咗呢種做法^[16]。

模擬訊號

任天堂 Switch 嘅手掣；手掣上面有好多個掣同搖桿，等玩家用手指嘅活動俾輸入。

模擬訊號（analog，粵拼：en1 naa4 lok4）嘅數值係連續嘅，是但兩個可能數值，嗰兩個數值之間原則上都實會有某啲可能數值，小數點後嘅位理論上可以無限加－即係同某啲物理量相模擬^{[註 3]}。模擬訊號相對於數碼訊號^[14]^[17]。

舉例說明，想像一部遊戲機嘅控制器：喺典型嘅遊戲控制器上面，控制器會有若干個掣同若干條搖桿；個控制器會以某啲方式駁住部遊戲機，係噉傳訊號去部機嗰度，話俾部機知玩家撳咗邊個掣；某個掣所傳嘅訊號係數碼訊號，因為個掣傳嘅訊號得嗰兩可能數值，撳咗同冇撳；相比之下，搖桿所傳嘅就係模擬訊號－是但搵條搖桿，設 x 同 y 為佢嘅坐標，理論上，x 同 y 嘅數值喺小數點後可以有幾多個位都得^[16]^{[註 4]}。然後個遊戲程式就可以按呢種資訊嚟行事，想像以下呢段簡化嘅虛擬碼：

 如果 玩家撳咗對應跳嗰個掣，
   玩家角色以 z 咁多嘅速度向上郁；
 玩家角色沿 X 軸嘅速度 += x
 玩家角色沿 Y 軸嘅速度 += y

同數碼訊號比，模擬訊號有好有唔好：原則上，模擬訊號有無限個可能數值－1, 1.01, 1.001, 1.0001... ，喺完美（冇雜音）嘅世界當中，個別嘅模擬訊號可以傳極大量資訊，而個別數碼訊號因為可能值有限，所以傳到嘅資訊量都有限；但現實係唔完美嘅，訊號嘅物理數值實會因為干擾等嘅原因而走樣，所以模擬訊號基本上實係唔完全準嘅－呢點令到模擬訊號唔能夠用於某啲要求極高準確度嘅醫療或者科研用途^[16]。

按函數嚟分

單位階躍

單位階躍函數呢個函數其中一條可能嘅式如下：

u={\begin{cases}0,&t<0,\\1,&t\geq 0,\end{cases}}

；

如果 u 做 Y 軸，t 做 X 軸，呢個單位階躍函數幅圖係

單位階躍函數可以用嚟表達有冇插掣嘅訊號：假想有部機械，個用家將佢個插頭插落個插蘇嗰度；插入去嗰一刻個時間點當做 0，u 就可以當做有冇電到，1 代表有電，0 代表冇電。

斜坡

斜坡函數其中一條可能嘅式如下：

u:={\begin{cases}t,&t\geq 0;\\0,&t<0\end{cases}}

；

如果 u 做 Y 軸，t 做 X 軸，呢個斜坡函數幅圖係

斜坡函數可以攞嚟表達（例如）下跌緊嘅物件嘅速度：假想有嚿物件，喺重力影響下向下跌；開始跌嗰刻個時間點當做 0，u 就可以當做佢嘅速度。詳情可以睇睇牛頓力學。

正弦

正弦函數專門攞嚟模擬一啲會週期性噉上上落落嘅變數，最基本嗰條式如下^[18]：

y(t)=A\sin(2\pi ft+\varphi )=A\sin(\omega t+\varphi )

；

呢條式畫做圖嘅話：

可以用正弦函數模擬嘅訊號，包括有電磁波以及腦電圖（EEG）所量度到、喺頭皮表面嘅微電壓呀噉。

時間離散度

時間離散度可以攞嚟將訊號分類，將訊號分做

連續時間（CT）同
離散時間（DT）

兩大類。喺數學定義上， CT 訊號嘅時間點係小數點後幾多個位都得，而 DT 訊號嘅時間點係離散嘅：量度 CT 訊號要無時無刻係噉一路觀察住，而量度 DT 訊號就係每隔若干單位時間觀察一次，譬如有個每 1 秒觀察一次嘅 DT 訊號，若果將第一次量度嘅時間點設做 0，會量度到喺時間點 1 秒同 2 秒嘅訊號，但就唔會準確知道時間點 2.5 秒嘅訊號係乜^[19]^[20]。想像下圖，灰色線嘅係一個 CT 訊號，而紅色線嘅係一個 DT 訊號。個 DT 訊號淨係每隔一段時間先會做量度：

人可以探測到嘅訊號都係屬 DT 嘅：喺現實應用中，冇感應器勁到能夠喺任何時間點一路觀察住個訊號，感應器頂攏可以做到（例如）每 1 毫秒量度一次，呢個感應器俾嘅輸出望落似 CT 訊號，但查實只係一個每次量度嘅時間差極細嘅 DT 訊號。大自然會對人類傳各種理論上係 CT 嘅訊號，人造嘅感應器會由呢啲訊號嗰度抽樣，抽出一串串 DT 訊號，用一串串每次量度嘅時間差極細嘅 DT 訊號，嚟趨近 CT 訊號^[19]^[21]。

下圖表達點樣用一個 DT 數碼訊號趨近 CT 模擬訊號，當中橙色線係 DT 數碼訊號，灰色線係 CT 模擬訊號：

訊號處理

訊號處理係工程學嘅子領域，喺好多現代科技當中都會用到，諸如電腦、收音機、影片同手機等現代社會必需嘅技術，冚唪唥都係因為有訊號處理先造到出嚟。對訊號處理嘅研究會用數學模型，模擬用嚟做訊號嘅物理量嘅傳播同變化，點樣用各種嘅機制轉化訊號，並且思考做訊號處理嘅機械要點設計至可以令訊號嘅傳遞更快捷同準確^[22]。

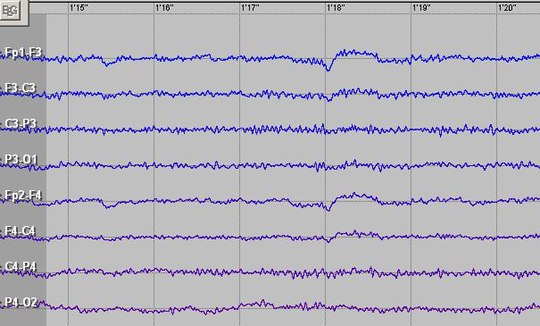
例如腦電圖（EEG）噉：

EEG 係神經科學同相關領域上成日用嘅神經造影技術，原理簡單講如下：腦做親啲乜嗰陣，佢裏面嗰啲數以億計嘅神經元都會用好微弱嘅電流嚟互傳資訊，電流改變會引致電壓改變，而唔同嘅腦活動牽涉嘅資訊都唔同－即係話個腦做唔同嘅功能嗰時，佢入面嗰啲電流同電壓改變嘅規律都會唔同；EEG 最常見嘅做法係將一啲特製嘅電極黐喺受試者嘅頭皮表面，量度頭皮嘅微弱電壓，微弱到通常以微伏特（μV；1 μV 相當於 10^-6 伏特）計；如是者，每條電極都會向量度架生提供量度到嘅微電壓呢個訊號^[23]。

EEG 訊號處理係腦電研究上嘅重要課題：一般嚟講，電極嘅訊號會傳去電腦度，然後電腦會用特定嘅演算法轉化訊號，令啲訊號變成對人類嚟講易睇嘅樣。例：

研究者做咗 10 分鐘長嘅 EEG 實驗，期間擺咗 19 條電極喺受試者頭上面，最起始嘅數據包含每條電極喺每個時間點嘅電壓值（一大列 $V_{lt}$ ， $V_{lt}$ 係指位置 l 喺時間點 t 嘅電壓，以向量代表^{[註 5]}；
轉化訊號：研究者要部電腦放棄頭嗰 1 分鐘同最尾嗰 1 分鐘嘅數據，理由係最頭同最尾嘅 EEG 數據最易受雜音干擾。
再轉化：跟住電腦會做傅立葉變換－簡單講就係將每個上上落落嘅腦電數據拆開，變成組成佢嘅波，估計每個頻率嘅腦電波嘅波幅同相位；
最後就可以做統計分析，例如睇吓每個頻率嘅腦電波嘅波幅，同邊啲行為有相關^[24]。

典型嘅腦電圖；X 軸係時間，Y 軸係電壓。上面呢幅有多條線，噉係因為個研究者度咗頭好多唔同位置嘅微電壓，每條線代表咗個頭某個位置嘅微電壓隨時間嘅改變。

傳輸協議

網絡傳輸協議係現代電子工程一個重要課題。現代電子工程會運用物理學上對電嘅認識，鑽研點樣有效噉用電做數據傳輸。舉個簡單例子說明，想像家陣喺地球唔同角落嘅幾個地方，彼此之間駁好咗電纜，冇得直接互相對話，但可以彼此之間傳電訊號；於是佢哋事先講好一套方案，簡化講可以想像^[25]：

佢哋用電纜傳訊號，每個訊號會係電壓（用嚟做訊號嘅物理量），如果個電壓值細過 $V_{t}$ ，就當個訊號係 0，否則就當個訊號係 1（數碼訊號）；
一串完整嘅訊號會由 n 個訊號組成，而 n實會係 7 嘅倍數（如果有個人收到串訊號，訊號數量唔係 7 嘅倍數，就表示串訊號實係出咗錯）；
串訊號當中每 7 個位都代表一個字母－100 0001 代表 A、100 0010 代表 B、100 0011 代表 C... 等等（解讀訊號嘅方案；詳情可以睇 ASCII）；
工程師整咗傳訊機，用家可以喺上面撳鍵盤，每個掣駁住一個電路，個 A 掣會令部機傳出 100 0001、個 B 掣會令部機傳出 100 0010... 等等（按解讀方案將資訊變成訊號嘅機制）；
工程師又整咗一部收訊機，當部機收到一串冇出錯嘅訊號嗰時，會喺一個熒幕上顯示相應嗰串英文字母（按訊號同解讀方案重砌返個資訊出嚟嘅機制）^[4]。

製作網絡傳輸協議嘅成個過程需要用同考慮好多元件，包括用嚟做訊號嘅物理量、公認嘅解讀方案講明邊個物理量規律表示邊個資訊、按解讀方案將資訊變成訊號嘅機制、以及按訊號同解讀方案重砌返個資訊出嚟嘅機制... 等等^[22]。而同通訊相關嘅工程學嘅研究重點之一就在於要點設計網絡傳輸協議，先可以令通訊嘅效率最大化。呢類研究對現代社會嘅運作嚟講不可或缺^[26]。

睇埋

文獻

歐美文獻：

Blahut, R. E. (2010). Fast algorithms for signal processing. Cambridge University Press.
Granlund, G. H., & Knutsson, H. (2013). Signal processing for computer vision. Springer Science & Business Media.
Hsu, P. H. Schaum's Theory and Problems: Signals and Systems, McGraw-Hill 1995, ISBN 0-07-030641-9
Lathi, B.P., Signal Processing & Linear Systems, Berkeley-Cambridge Press, 1998, ISBN 0-941413-35-7
Shannon, C. E., 2005 [1948], "A Mathematical Theory of Communication," (corrected reprint), accessed Dec. 15, 2005. Orig. 1948, Bell System Technical Journal, vol. 27, pp. 379–423, 623-656.

註釋

↑ 由呢個定義睇得出，訊號未必係人造嘅。呢篇文集中講工程學嗰啲人造訊號。至於有關非人造訊號嘅例子，可以睇吓訊號理論呢個進化生物學理論：個理論有研究生物物種之間同個體之間嘅訊號。
↑ 可以睇吓 ASCII。
↑ 參見英文：analogous
↑ 不過喺實際應用上，由於電腦記憶體能力所限，部遊戲機嘅電腦記到嘅數可以有幾多個位，都會係有限嘅。
↑ 可以睇埋時間序列。

引咗

↑ ^1.0 ^1.1 ^1.2 Pragnan Chakravorty, "What Is a Signal? [Lecture Notes]," IEEE Signal Processing Magazine, vol. 35, no. 5, pp. 175-177, Sept. 2018，原文對訊號嘅定義："a function that conveys information"
↑ Roland Priemer (1991). Introductory Signal Processing. World Scientific. p. 1.
↑ Poisel, R. A. (2008). Introduction to communication electronic warfare systems. Artech House, Inc..
↑ ^4.0 ^4.1 Alley, C. L., & Atwood, K. W. (1973). Electronic engineering. Wiley.
↑ Some authors do not emphasize the role of information in the definition of a signal. For example, see Priyabrata Sinha (2009). Speech processing in embedded systems. Springer. p. 9. ISBN 978-0387755809. Archived from the original on 2013-06-02. "To put it very generally, a signal is any time-varying physical quantity."
↑ "Aims and scope 互聯網檔案館嘅歸檔，歸檔日期2019年9月27號，.". IEEE Transactions on Signal Processing. IEEE.
↑ Stanislaw, H., & Todorov, N. (1999). Calculation of signal detection theory measures. Behavior research methods, instruments, & computers, 31(1), 137-149.
↑ Mathematical Description of Continuous-Time Signals 互聯網檔案館嘅歸檔，歸檔日期2019年10月3號，. (PDF).
↑ T. H. Wilmshurst (1990). Signal Recovery from Noise in Electronic Instrumentation (2nd ed.). CRC Press. pp. 11 ff.
↑ Robert K. Dueck. Digital Design with CPLD Applications and VHDL. "A digital representation can have only specific discrete values."
↑ Analogue and Digital Communication Techniques. Archived from the original on 2017-12-17. "A digital signal is a complex waveform and can be defined as a discrete waveform having a finite set of levels."
↑ Paul Horowitz; Winfield Hill (2015). The Art of Electronics. Cambridge University Press.
↑ Proakis, John G.; Manolakis, Dimitris G. (2007-01-01). Digital Signal Processing. Pearson Prentice Hall.
↑ ^14.0 ^14.1 Horowitz, Paul; Hill, Winfield (1989). The Art Of Electronics, 2nd Ed. Cambridge University Press. pp. 471-473.
↑ Robert K. Dueck. Digital Design with CPLD Applications and VHDL. "A digital representation can have only specific discrete values."
↑ ^16.0 ^16.1 ^16.2 Hoeschele, D. F. (1994). Analog-to-digital and digital-to-analog conversion techniques (Vol. 968). New York: Wiley.
↑ Biolek, D., Senani, R., Biolkova, V., & Kolka, Z. (2008). Active elements for analog signal processing: classification, review, and new proposals. Radioengineering, 17(4), 15-32.
↑ "Sinusoid". Encyclopedia of Mathematics. Springer.
↑ ^19.0 ^19.1 Sarpturk, S. Z., Istefanopulos, Y., & Kaynak, O. (1987). On the stability of discrete-time sliding mode control systems. IEEE Transactions on Automatic Control, 32(10), 930-932.
↑ Vinod Kumar Khanna, Digital Signal Processing: "A digital signal is a special form of discrete-time signal which is discrete in both time and amplitude, obtained by permitting each value (sample) of a discrete-time signal to acquire a finite set of values (quantization), assigning it a numerical symbol according to a code ... A digital signal is a sequence or list of numbers drawn from a finite set."
↑ Discrete Time Processing of Continuous Time Signals 互聯網檔案館嘅歸檔，歸檔日期2019年10月19號，..
↑ ^22.0 ^22.1 Alan V. Oppenheim and Ronald W. Schafer (1989). Discrete-Time Signal Processing. Prentice Hall. p. 1.
↑ Niedermeyer E.; da Silva F.L. (2004). Electroencephalography: Basic Principles, Clinical Applications, and Related Fields. Lippincott Williams & Wilkins.
↑ Fiscon, G., Weitschek, E., Cialini, A., Felici, G., Bertolazzi, P., De Salvo, S., ... & De Cola, M. C. (2018). Combining EEG signal processing with supervised methods for Alzheimer’s patients classification. BMC medical informatics and decision making, 18(1), 35.
↑ Freeman, Roger L. (1999). Fundamentals of Telecommunications. John Wiley & Sons, Inc.
↑ Brian W Marsden (1986): Communication network protocols, 2nd Edition. Chartwell Bratt,

拎

維基同享中有關訊號嘅資源類
（英文）Journal of Signal Processing，研究訊號處理嘅期刊。
（英文）Journal of Signal Processing Systems，研究訊號處理系統嘅期刊。

[9] 由呢個定義睇得出，訊號未必係人造嘅。呢篇文集中講工程學嗰啲人造訊號。至於有關非人造訊號嘅例子，可以睇吓訊號理論呢個進化生物學理論：個理論有研究生物物種之間同個體之間嘅訊號。

[13] 可以睇吓 ASCII。

[19] 參見英文：analogous

[21] 不過喺實際應用上，由於電腦記憶體能力所限，部遊戲機嘅電腦記到嘅數可以有幾多個位，都會係有限嘅。

[28] 可以睇埋時間序列。

[pragnan2018-1] 1.0 ^1.1 ^1.2 Pragnan Chakravorty, "What Is a Signal? [Lecture Notes]," IEEE Signal Processing Magazine, vol. 35, no. 5, pp. 175-177, Sept. 2018，原文對訊號嘅定義："a function that conveys information"

[2] Roland Priemer (1991). Introductory Signal Processing. World Scientific. p. 1.

[3] Poisel, R. A. (2008). Introduction to communication electronic warfare systems. Artech House, Inc..

[alley1973-4] 4.0 ^4.1 Alley, C. L., & Atwood, K. W. (1973). Electronic engineering. Wiley.

[5] Some authors do not emphasize the role of information in the definition of a signal. For example, see Priyabrata Sinha (2009). Speech processing in embedded systems. Springer. p. 9. ISBN 978-0387755809. Archived from the original on 2013-06-02. "To put it very generally, a signal is any time-varying physical quantity."

[6] "Aims and scope 互聯網檔案館嘅歸檔，歸檔日期2019年9月27號，.". IEEE Transactions on Signal Processing. IEEE.

[7] Stanislaw, H., & Todorov, N. (1999). Calculation of signal detection theory measures. Behavior research methods, instruments, & computers, 31(1), 137-149.

[chaptercontsignal-8] Mathematical Description of Continuous-Time Signals 互聯網檔案館嘅歸檔，歸檔日期2019年10月3號，. (PDF).

[10] T. H. Wilmshurst (1990). Signal Recovery from Noise in Electronic Instrumentation (2nd ed.). CRC Press. pp. 11 ff.

[11] Robert K. Dueck. Digital Design with CPLD Applications and VHDL. "A digital representation can have only specific discrete values."

[12] Analogue and Digital Communication Techniques. Archived from the original on 2017-12-17. "A digital signal is a complex waveform and can be defined as a discrete waveform having a finite set of levels."

[paulhill2015-14] Paul Horowitz; Winfield Hill (2015). The Art of Electronics. Cambridge University Press.

[15] Proakis, John G.; Manolakis, Dimitris G. (2007-01-01). Digital Signal Processing. Pearson Prentice Hall.

[horowitz1989-16] 14.0 ^14.1 Horowitz, Paul; Hill, Winfield (1989). The Art Of Electronics, 2nd Ed. Cambridge University Press. pp. 471-473.

[dueck-17] Robert K. Dueck. Digital Design with CPLD Applications and VHDL. "A digital representation can have only specific discrete values."

[hoeschele1994-18] 16.0 ^16.1 ^16.2 Hoeschele, D. F. (1994). Analog-to-digital and digital-to-analog conversion techniques (Vol. 968). New York: Wiley.

[20] Biolek, D., Senani, R., Biolkova, V., & Kolka, Z. (2008). Active elements for analog signal processing: classification, review, and new proposals. Radioengineering, 17(4), 15-32.

[22] "Sinusoid". Encyclopedia of Mathematics. Springer.

[dis-23] 19.0 ^19.1 Sarpturk, S. Z., Istefanopulos, Y., & Kaynak, O. (1987). On the stability of discrete-time sliding mode control systems. IEEE Transactions on Automatic Control, 32(10), 930-932.

[24] Vinod Kumar Khanna, Digital Signal Processing: "A digital signal is a special form of discrete-time signal which is discrete in both time and amplitude, obtained by permitting each value (sample) of a discrete-time signal to acquire a finite set of values (quantization), assigning it a numerical symbol according to a code ... A digital signal is a sequence or list of numbers drawn from a finite set."

[25] Discrete Time Processing of Continuous Time Signals 互聯網檔案館嘅歸檔，歸檔日期2019年10月19號，..

[oppenheim1989-26] 22.0 ^22.1 Alan V. Oppenheim and Ronald W. Schafer (1989). Discrete-Time Signal Processing. Prentice Hall. p. 1.

[Nide-27] Niedermeyer E.; da Silva F.L. (2004). Electroencephalography: Basic Principles, Clinical Applications, and Related Fields. Lippincott Williams & Wilkins.

[29] Fiscon, G., Weitschek, E., Cialini, A., Felici, G., Bertolazzi, P., De Salvo, S., ... & De Cola, M. C. (2018). Combining EEG signal processing with supervised methods for Alzheimer’s patients classification. BMC medical informatics and decision making, 18(1), 35.

[30] Freeman, Roger L. (1999). Fundamentals of Telecommunications. John Wiley & Sons, Inc.

[31] Brian W Marsden (1986): Communication network protocols, 2nd Edition. Chartwell Bratt,

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[註 1]

[9]

[10]

[11]

[註 2]

[12]

[13]

[14]

[15]

[16]

[註 3]

[17]

[註 4]

[18]

[19]

[20]

[21]

[22]

[23]

[註 5]

[24]

[25]

[26]

睇傾改資訊理論
資訊通訊同資訊處理 Signal（數碼定模擬）雜音訊號對雜訊比例 Bit 相似度量度資訊熵（聯合熵 · 條件熵 · 相互資訊 · 條件相互資訊 · 相對熵）熵率資訊最大化原則
第啲概念概率論（不確定性 · 概率）編碼理論（雜訊通道編碼定理）數據壓縮（率失真理論 · 無雜訊編碼定理）頻道（二元對稱同二元消除 · 容量）
相關領域電腦科學（密碼學 · 資訊系統）電子工程同電訊認知科學（神經科學）語言學統計學模控學資訊經濟學
拉雜相關貝葉斯推論演算法熵赤池同貝葉斯資訊量準則擬亂數產生同隨機種子控制系統資訊過多認知同神經編碼