蒙地卡羅樹搜尋

蒙地卡羅樹搜尋(英文:Monte Carlo tree search,簡稱 MCTS)係一種搜尋演算法,用嚟幫一位決策者(例如一個 AI 程式)喺有極高複雜度嘅決策情境下搵出「最啱」嘅選擇[1][2]。
例如依家教一個人工智能程式捉棋:現實世界嘅棋類遊戲好多時都複雜得好交關;譬如係圍棋噉,圍棋個棋盤有成 10170 個可能形勢咁多;事實表明,就算用好先進嘅電腦嚟推算形勢,都要嘥極大量嘅時間先至能夠睇勻晒所有嘅可能性,人工智能程式做唔到「响夠短嘅時間內俾答案」。所以喺實際應用上,靠窮舉式(指考慮晒一切可能性再揀個最好嘅選擇)行事嘅演算法就唔掂[3]。
於是,廿一世紀初嘅遊戲人工智能領域就有咗 MCTS 嘅諗法。簡單噉講,MCTS 旨在要由手上嘅可能性當中,有技巧噉揀一細部份嘅出嚟集中睇。行 MCTS 嘅程式會有一啲特定嘅方法決定「邊啲可能性最值得睇」,然之後佢哋就會集中分析呢啲可能性,噉就令到部電腦能夠喺相對短嘅時間內俾到個輸出[3]。喺 2010 年代後半橛 MCTS 呢個諗法經已成功咁嚌,例如人工智能程式 AlphaGo 就用咗 MCTS,並且喺 2016 年打低九段圍棋棋手李世石而出咗名[4][5]。
背景概念
[編輯]應付嘅問題
[編輯]蒙地卡羅樹搜尋係一種用嚟應付複雜決策問題嘅技術。想像一樖決策樹[e 1]。決策樹係一種用嚟表示決策嘅圖:一樖決策樹(下圖係例子)會有若干個節點[e 2],每個節點(下圖啲黑色框框)代表咗一個決策點,會有若干個箭咀指去下一排節點(下一步),每一個箭咀表示「如果揀咗呢個選項,就去呢個決策點」。即係話下圖嗰樖決策樹表示:
- 個決策者家陣想決定「好唔好去玩」(PLAY),
- 喺開頭個節點,去玩(play)嘅價值有 9 分,唔好去玩(don't play)嘅價值有 5 分,
- 然後睇天氣(OUTLOOK),如果晴天(sunny),噉去玩嘅價值變成 2 分,唔好去玩嘅價值變成 3 分,
- 然後個決策者會睇濕度(HUMIDITY)
... 如此類推[1]。

以下係井字過三關樖決策樹嘅其中一橛:

決策樹喺教 AI 玩遊戲嘅研究上頗受重視:一隻遊戲可以想像成一樖決策樹,喺任何一個時間點會處於某個特定嘅狀態,玩家嘅決策會決定遊戲狀態跟住落嚟會變成咩樣;原則上,教 AI 玩遊戲可以想像成「用搜尋演算法[e 3]由一樖決策樹嗰度搵出最好嘅選擇」。問題係,現實世界會有人玩嘅遊戲,啲決策樹通常都複雜得好交關,例如國際象棋喺兩位棋手都行咗第一步之後,個棋盤會有 400 個可能嘅形勢,而喺兩個棋手都行咗第二步之後,個棋盤會有 197,742 個可能嘅形勢,等到兩人都行咗第三步之後,呢個數字會超過 100 萬;圍棋就更加複雜,有成 10170 個可能形勢咁多。因為呢啲遊戲咁複雜,窮舉搜尋[e 4]喺實際應用上根本行唔通,做唔到喺有限嘅時間內計到個答案[6][7]。

個諗頭點嚟
[編輯]
蒙地卡羅方法[e 5]係蒙地卡羅樹搜尋嘅一個重要基礎。蒙地卡羅方法源於 1940 年代,泛指一類嘅演算法,特徵係會用帶有隨機性嘅做法嚟應付決定型系統[e 6]:如果話一個系統係「決定型」嘅,簡單講係話呢個系統冇隨機性喺裏面,但就算一個系統係決定型嘅,佢依然有可能會係複雜到難以用決定型嘅方法解決[8]。
- 界定個系統嘅輸入嘅可能數值(定義域[e 7]);
- 用一個表示輸入數值、受定義域限制嘅概率分佈[e 8]隨機噉產生一個輸入;
- 對個輸入做決定型嘅運算;
- 將步驟 2 同 3 重複 咁多次,得到 個輸出,再結合數據[e 9])-例如計嗰 個輸出嘅平均值。
舉個簡單例子說明,蒙地卡羅方法可以用嚟估計圓周率()嘅數值[9]:
- 畫一個正方形,再喺個正方形入面畫個 90° 嘅扇形,任何嘅輸入坐標 都實會喺個正方形裏面(定義域);
- 用一個均勻分佈[e 10]產生一個輸入坐標數值,「均勻分佈」意思係指每個坐標可能數值出現嘅機率都完全一樣(睇埋隨機數生成);
- 喺產生咗嘅輸入坐標數值嘅位置嗰度畫一點(做運算);
- 將步驟 2 同 3 重複 咁多次,最後數吓有幾多點點係喺個扇形裏面(同原點距離細過 1)嘅,設呢個數值做 ,如果 嘅數值大到接近無限大嘅話,以下呢樣嘢會成立:
蒙地卡羅方法帶出咗一個諗法:無論一個系統係咪決定型嘅都好,用帶有隨機性嘅方法都有可能俾得到有返咁上下準嘅答案-「有返咁上下準」意思係指,得出嘅答案同真實嘅答案唔係爭咁遠,未至於大到能夠對解決問題嘅效率造成明顯嘅負面影響[8]。即係話,應付國際象棋呢啲決定型嘅遊戲(玩家唔會用擲骰仔等有隨機性嘅方法決定點行)嘅決策樹嗰陣,都有可能可以用帶有隨機性嘅演算法嚟解[11][12]。
運作原理
[編輯]玩到尾
[編輯]
想像玩到尾[e 11]呢個概念。喺最基本上,家陣個人工智能程式做以下嘅步驟[4]:
- 由可能嘅選擇(樖決策樹嘅下一排節點)當中隨機揀(
select,粵拼:si6 lek1)一個出嚟; - 將呢柞節點「玩到尾」-以某啲方式(
roll,粵拼:rou1)估計呢個節點最後結果會係乜(輸定贏),簡單例子有
噉就算係一次玩到尾。响最簡單嗰種情況下,個演算法可以每次自己要做決定(例:到自己行)嗰陣,都
比較進階嘅演算法,仲會有更複雜嘅方法做 select 同 roll,而 select 同 roll 當中嘅技巧就係蒙地卡羅樹搜尋最重要嘅一環之一[14]。
四大步驟
[編輯]最基本上,用蒙地卡羅樹搜尋搵出「應該行邊步」嘅過程有若干個回合,每個回合有四個步驟[15]:
- 選擇[e 13]:設 呢個節點做起點(代表遊戲嘅現時狀態),並且由下一排節點嗰度揀一個(
select),揀 排( 係一個可以預先設定嘅數值),設 做最後去到嗰個節點;選擇嘅過程會涉及所謂嘅利用定係探索[e 14]之間嘅取捨[16]-- 利用係指揀最「好」(根據過往經驗最能夠提升贏面)嗰啲選擇,
- 探索就係指睇一啲冇咁「好」(唔係最「好」但睇咗可能會摷到進一步提升贏面嘅選項)嗰啲選擇。
- 擴張[e 15]:除非 會令遊戲結束(定咗勝負或者打和),由 嘅下一排節點當中揀一個,設呢個節點做 ;
- 模擬[e 16]:由 嗰度做一次玩到尾嘅過程;
- 反向傳播[e 17]:用玩到尾嘅結果改變自己對 同 之間嗰條路線嘅判斷;例:如果模擬步驟發現 最後會大機會令到自己贏,就將 同 之間嗰條路線或者節點 加若干分數(),而一個節點愈高分,個程式就愈大可能會揀行嗰步[17]。亦都可以睇埋最大最小化等嘅決策法則。
- 順帶一提,有進階嘅做法會係教個 AI「喺唔同時候採取唔同嘅決策法則」或者「行完一輪之後攞走某啲諗過、但發覺冇用嘅節點」[15]:p. 7-9。
以下係呢個基本演算法嘅圖解(英文)。幅圖表示緊一樖玩國際象棋嘅決策樹,每個圓圈係一個節點,白色圓圈表示白棋嗰方嘅選擇,而深色圓圈表示黑棋嗰方嘅選擇,白色同黑色輪流行;每個節點掕住嘅份數表示嗰個節點(按過往嘅模擬)有幾大機會會令嗰一方贏(例:最頂嗰個節點開頭係白色掕住「11/21」,表示個程式對呢個節點做咗 21 次玩到尾,當中 11 次係白色贏):

利用定探索
[編輯]喺蒙地卡羅樹搜尋嘅第一步(選擇)當中,其中一個最大嘅問題係「要點樣平衡利用同探索[e 14]」:一方面,利用能夠响短期內令自己利益最大化:集中淨係揀一啲「根據過往經驗,大機會贏」嘅選擇;不過另一方面,蒙地卡羅樹搜尋必然涉及由數唔晒咁多個選擇當中揀一啲出嚟,所以喺任何一點時間都實會有大量嘅可能性係決策者未睇過嘅,去探索呢啲可能性,有一定嘅機會搵到能夠進一步提升贏面嘅選擇[16];所以蒙地卡羅樹搜尋嘅研究者就喺度諗[18][19]-
到底一個蒙地卡羅樹搜尋程式應該乜嘢時候集中『利用』乜嘢時候集中『探索』?
設 做有得揀嘅節點嘅集,家陣個程式變成想令以下呢條式得出嘅數值有咁大得咁大[4]:
- ;,當中
- 係節點 睇咗幾多次。
- 係節點 嘅模擬當中「贏」發生咗幾多次。
- 「」(或者 )反映節點 根據過往經驗有幾大機會贏(可以睇返上面反向傳播)。
- 係依家身處嗰個節點睇咗幾多次。
- 係自然對數。
- 「」反映節點 有幾少可睇, 數值愈細 就會愈大。
- 係所謂嘅探索參數[e 18],係一個數值可以用實驗嚟調節嘅參數。
用日常用語講即係話:喺呢條式之下,得分最高嘅節點-個程式最有可能會睇嘅節點-傾向會係「根據過往經驗有大機會贏」(要利用)或者「過往最少睇」(要探索)嘅節點[註 2][15]。
輕度定重度
[編輯]蒙地卡羅樹搜尋嘅改良版,會分辨所謂嘅輕度玩到尾[e 19]同埋重度玩到尾[e 20][20][21][22]:
- 「輕度玩到尾」指玩到尾嘅過程完全係隨機嘅-模擬「呢個節點會引致乜嘢結果」嗰陣,個程式齋靠每步隨機是但噉行;
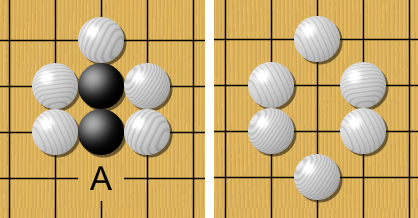
- 「重度玩到尾」指玩到尾嘅過程會用到常用嘅捷思法-即係用一啲已知嘅常用解難步驟(捷思法)嚟行。喺呢方面,個程式嘅設計者好可能會靠參考由專業玩隻遊戲嘅人提供嘅專家知識:喺專業捉棋或者玩第啲遊戲嘅人之間,好多時都會有啲所謂嘅行內捷思法,即係「噉行法傾向會贏」嘅簡單法則,而研究者可以試吓教一個人工智能程式做重度玩到尾嗰時用呢啲法則嚟模擬「呢個節點會引致乜嘢結果」。例如喺圍棋入面,一條簡單嘅捷思法係「用自己啲棋將對手圍住」,而因為呢條捷思法相對簡單,做起玩到尾模擬嗰陣部電腦就唔使用咁多運算資源[23][24]。
喺 2010 年代初,用重度玩到尾嘅蒙地卡羅樹搜尋經已有初步嘅成功,喺一啲人工智能玩遊戲比賽當中打贏[20]。
RAVE
[編輯]蒙地卡羅樹搜尋嘅改良版,好多時仲會用埋所謂嘅快速行動價值估計[e 21]做法:一般嘅蒙地卡羅樹搜尋要花一段時間(若干個回合)嚟做模擬,先至會得出每個節點嘅價值;而喺呢一點之前,個蒙地卡羅樹搜尋演算法嘅行動會近乎隨機。想像有樖決策樹,當中有個節點 , 有一個子節點 ,個程式儲起咗 嘅價值(),而 呢個數值包含咗兩樣嘢[22]:
- 喺打前嘅玩到尾當中贏咗幾多次,而且仲包埋
- 所有起自 終於 嘅「玩到尾贏出次數」。
RAVE 呢種做法係考慮到一點:喺好多遊戲當中,是但搵某一個「遊戲狀態改變」,個改變通常都係可以透過多條圖徑達致嘅;所以如果做咗一個節點嘅玩到尾,估計到佢個價值,噉呢個結果理應唔淨只可以反映個節點本身嘅價值,仲會反映相連節點嘅價值。用咗 RAVE,個程式能夠快啲知道每個節點嘅價值,所以可以加快「估計啲節點嘅價值」嘅過程[22]。
以下圖為例,想像以下呢樖井字過三關決策樹,每個節點表示「邊方霸咗邊個格仔」(例:×a1 表示「交叉霸咗 a1 嗰格」)。如果個程式係用 RAVE 嘅,而起始點係最開始嗰點(空嘅),做咗 b1-a2-b3 嘅玩到尾模擬之後,啲紅線掂嘅節點嘅價值全部都會受到更新。

响實際應用上,可以想像成將 嗰條式改吓,變成類似以下噉嘅樣,照舊係要個程式揀條式個數值最大嘅節點[25]:
- ;,當中
- 係指包含咗節點 喺入面嘅玩到尾嘅數量。
- 係指包含咗節點 喺入面嘅玩到尾總共贏咗幾多次。
- 反映總共做咗幾多次模擬;
- 係一個函數, 數值細 會接近 1,而 數值大 會接近 0。
起源
[編輯]蒙地卡羅樹搜尋嘅技術起源於 2000 年代中:喺 2006 年,有法國嘅人工智能研究者受到蒙地卡羅方法啟發,將蒙地卡羅方法應用嚟搜尋遊戲嘅決策樹-輸入可能值:目前狀態去得嘅節點;隨機產生輸入:是但攞一個節點嚟睇;計輸出:「個節點會輸定贏」... 重複若干次-並且用蒙地卡羅樹搜尋呢個詞嚟形容佢個演算法做緊嘅嘢[26]。佢嗰個做法話咁快就引起咗當時學界嘅注意,吸引第啲研究者仿傚同埋嘗試改善佢嗰個演算法,而呢啲程式仲取得咗初步嘅成功,喺簡化版嘅圍棋當中打低咗業餘嘅棋手[27][28]。
蒙地卡羅樹搜尋係喺 2010 年代開始進入全盛嘅:喺 2015 年 10 月,由 Google DeepMind 開發嘅捉圍棋程式 AlphaGo 成為咗第一個成功噉响「個人類棋手冇讓賽」嘅情況下打低專業人類棋手嘅人工智能程式[29],而及後 AlphaGo 仲同韓國嘅九段(最高級)圍棋棋手李世石比賽,捉咗 5 局,並且以 4 比 1 大獲全勝,令到 AlphaGo 相關嘅技術(包括蒙地卡羅樹搜尋)一舉成名[30][31]。自此之後,蒙地卡羅樹搜尋嘅技術受到人工智能界嘅關注,仲俾人廣泛噉攞嚟教人工智能玩各種圍棋以外嘅圖板遊戲[32][33][34],甚至乎係即時制嘅視像遊戲[35][36]同埋帶有隨機性嘅桌上遊戲[37][38]。
程式
[編輯]- AlphaGo:用到蒙地卡羅樹搜尋、強化學習同深度學習,玩嘅係圍棋。
- AlphaGo Zero:AlphaGo 嘅進化版,出名在唔使用到任何人類捉棋數據,而且仲打低咗之前嘅 AlphaGo 程式[39]。
- AlphaZero:廣義化嘅 AlphaGo,都係用蒙地卡羅樹搜尋、強化學習同深度學習,但除咗圍棋之外仲識捉國際象棋同日本將棋[40]。
- Leela Chess Zero:一隻自由開源軟件,用 AlphaZero 嘅方法捉國際象棋。
睇埋
[編輯]註釋
[編輯]參攷
[編輯]本文用咗嘅專業詞彙,英文版本如下:
- ↑ decision tree
- ↑ node
- ↑ search algorithm
- ↑ brute-force search:最夾硬嚟嗰種做法-將啲可能性冚唪唥睇勻晒佢,再揀最好嗰個。
- ↑ Monte Carlo method
- ↑ deterministic system
- ↑ domain
- ↑ probability distribution
- ↑ aggregate data
- ↑ uniform distribution
- ↑ playout / roll-out
- ↑ artificial neural network
- ↑ selection
- ↑ 14.0 14.1 exploit or explore
- ↑ expansion
- ↑ simulation
- ↑ backpropagation
- ↑ exploration parameter
- ↑ light playout
- ↑ heavy playout
- ↑ rapid action value estimation,英文簡稱 RAVE
本文引用咗嘅文獻:
- ↑ 1.0 1.1 Cameron Browne; Edward Powley; Daniel Whitehouse; Simon Lucas; Peter I. Cowling; Philipp Rohlfshagen; Stephen Tavener; Diego Perez; Spyridon Samothrakis; Simon Colton (March 2012). "A Survey of Monte Carlo Tree Search Methods". IEEE Transactions on Computational Intelligence and AI in Games. 4 (1): 1–43.
- ↑ Monte Carlo Tree Search. Towards Data Science.
- ↑ 3.0 3.1 Silver, David; Huang, Aja; Maddison, Chris J.; ... et al. (28 January 2016). "Mastering the game of Go with deep neural networks and tree search". Nature. 529 (7587): 484–489.
- ↑ 4.0 4.1 4.2 4.3 Liu, Michael (10 October 2017). "General Game-Playing With Monte Carlo Tree Search". Medium.
- ↑ Bouzy, B., & Tutorial, C. (2007, April). Old-fashioned computer go vs monte-carlo go (PDF). In IEEE Symposium on Computational Intelligence in Games (CIG).
- ↑ Bontrager, P., Khalifa, A., Mendes, A., & Togelius, J. (2016, September). Matching games and algorithms for general video game playing. In Twelfth Artificial Intelligence and Interactive Digital Entertainment Conference.
- ↑ Kleinsmith, A., & Gillies, M. (2013). Customizing by doing for responsive video game characters. International Journal of Human-Computer Studies, 71(7-8), 775-784.
- ↑ 8.0 8.1 Kroese, D. P.; Brereton, T.; Taimre, T.; Botev, Z. I. (2014). "Why the Monte Carlo method is so important today". WIREs Comput Stat. 6 (6): 386–392.
- ↑ 9.0 9.1 Kalos, Malvin H.; Whitlock, Paula A. (2008). Monte Carlo Methods. Wiley-VCH.
- ↑ Abramson, B. (2014). The expected-outcome model of two-player games. Morgan Kaufmann.
- ↑ Wolfgang Ertel; Johann Schumann; Christian Suttner (1989). "Learning Heuristics for a Theorem Prover using Back Propagation.". In J. Retti; K. Leidlmair (eds.). 5. Österreichische Artificial-Intelligence-Tagung. Informatik-Fachberichte 208,pp. 87-95. Springer.
- ↑ Suttner, C., & Ertel, W. (1990, July). Automatic acquisition of search guiding heuristics. In International Conference on Automated Deduction (pp. 470-484). Springer, Berlin, Heidelberg.
- ↑ Gelly, S., Wang, Y., Munos, R., & Teytaud, O. (2006). Modification of UCT with patterns in Monte-Carlo Go (Doctoral dissertation, INRIA).
- ↑ Brügmann, Bernd (1993). Monte Carlo Go (PDF). Technical report, Department of Physics, Syracuse University.
- ↑ 15.0 15.1 15.2 Chaslot, G. M. J., Winands, M. H., HERIK, H. J. V. D., Uiterwijk, J. W., & Bouzy, B. (2008). Progressive strategies for Monte-Carlo tree search (PDF). New Mathematics and Natural Computation, 4(03), 343-357.
- ↑ 16.0 16.1 Kocsis, L., & Szepesvári, C. (2006, September). Bandit based monte-carlo planning. In European conference on machine learning (pp. 282-293). Springer, Berlin, Heidelberg.
- ↑ Coquelin, P. A., & Munos, R. (2007). Bandit algorithms for tree search (PDF). arXiv preprint cs/0703062.
- ↑ Auer, Peter; Cesa-Bianchi, Nicolò; Fischer, Paul (2002). "Finite-time Analysis of the Multiarmed Bandit Problem (PDF)" (PDF). Machine Learning. 47 (2/3): 235–256.
- ↑ Chang, Hyeong Soo; Fu, Michael C.; Hu, Jiaqiao; Marcus, Steven I. (2005). "An Adaptive Sampling Algorithm for Solving Markov Decision Processes 互聯網檔案館嘅歸檔,歸檔日期2021年4月20號,." (PDF). Operations Research. 53: 126–139.
- ↑ 20.0 20.1 Świechowski, M.; Mańdziuk, J. (2010). "Self-Adaptation of Playing Strategies in General Game Playing" (PDF), IEEE Transactions on Computational Intelligence and AI in Games, vol: 6(4), pp. 367-381.
- ↑ Seth Pellegrino; Peter Drake (2010). "Investigating the Effects of Playout Strength in Monte-Carlo Go". Proceedings of the 2010 International Conference on Artificial Intelligence, ICAI 2010, July 12–15, 2010, Las Vegas Nevada, USA. Hamid R. Arabnia, David de la Fuente, Elena B. Kozerenko, José Angel Olivas, Rui Chang, Peter M. LaMonica, Raymond A. Liuzzi, Ashu M. G. Solo (eds.). CSREA Press. pp. 1015–1018.
- ↑ 22.0 22.1 22.2 Gelly, Sylvain; Silver, David (2007). "Combining Online and Offline Knowledge in UCT" (PDF). Machine Learning, Proceedings of the Twenty-Fourth International Conference (ICML 2007), Corvallis, Oregon, USA, June 20–24, 2007. Zoubin Ghahramani (ed.). ACM. pp. 273–280.
- ↑ Drake, Peter (December 2009). "The Last-Good-Reply Policy for Monte-Carlo Go". ICGA Journal. 32 (4): 221–227.
- ↑ Rémi Coulom. "CLOP: Confident Local Optimization for Noisy Black-Box Parameter Tuning". ACG 2011: Advances in Computer Games 13 Conference, Tilburg, the Netherlands, November 20–22.
- ↑ David Silver (2009). Reinforcement Learning and Simulation-Based Search in Computer Go 互聯網檔案館嘅歸檔,歸檔日期2021年4月16號,. (PDF). PhD thesis, University of Alberta.
- ↑ Rémi Coulom (2007). "Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search". Computers and Games, 5th International Conference, CG 2006, Turin, Italy, May 29–31, 2006. Revised Papers. H. Jaap van den Herik, Paolo Ciancarini, H. H. L. M. Donkers (eds.). Springer. pp. 72–83.
- ↑ Chang-Shing Lee; Mei-Hui Wang; Guillaume Chaslot; ... et al. (2009). "The Computational Intelligence of MoGo Revealed in Taiwan's Computer Go Tournaments". IEEE Transactions on Computational Intelligence and AI in Games. 1 (1): 73–89.
- ↑ Markus Enzenberger; Martin Mūller (2008). Fuego - An Open-Source Framework for Board Games and Go Engine Based on Monte Carlo Tree Search (PDF). Technical report, University of Alberta.
- ↑ AlphaGo: Mastering the ancient game of Go with Machine Learning. Google AI Blog.
- ↑ "Google achieves AI 'breakthrough' by beating Go champion". BBC News.
- ↑ "Google AlphaGo AI clean sweeps European Go champion". ZDNet.
- ↑ Broderick Arneson; Ryan Hayward; Philip Henderson (June 2009). "MoHex Wins Hex Tournament" (PDF). ICGA Journal. 32 (2): 114–116.
- ↑ Timo Ewalds (2011). Playing and Solving Havannah (PDF). Master's thesis, University of Alberta.
- ↑ Tomáš Kozelek (2009). Methods of MCTS and the game Arimaa (PDF). Master's thesis, Charles University in Prague.
- ↑ Xiaocong Gan; Yun Bao; Zhangang Han (December 2011). "Real-Time Search Method in Nondeterministic Game – Ms. Pac-Man". ICGA Journal. 34 (4): 209–222.
- ↑ Tom Pepels; Mark H. M. Winands; Marc Lanctot (September 2014). "Real-Time Monte Carlo Tree Search in Ms Pac-Man". IEEE Transactions on Computational Intelligence and AI in Games. 6 (3): 245–257.
- ↑ Jonathan Rubin; Ian Watson (April 2011). "Computer poker: A review" (PDF). Artificial Intelligence. 175 (5–6): 958–987.
- ↑ C.D. Ward; P.I. Cowling (2009). "Monte Carlo Search Applied to Card Selection in Magic: The Gathering" (PDF). CIG'09 Proceedings of the 5th international conference on Computational Intelligence and Games. IEEE Press.
- ↑ Hassabis, Demis; Siver, David (18 October 2017). "AlphaGo Zero: Learning from scratch". DeepMind official website. Retrieved 19 October 2017.
- ↑ Knapton, Sarah; Watson, Leon (December 6, 2017). "Entire human chess knowledge learned and surpassed by DeepMind's AlphaZero in four hours". Telegraph.co.uk.
文獻
[編輯]可以進一步參考嘅文獻:
- Althöfer, Ingo (2012). "On Board-Filling Games with Random-Turn Order and Monte Carlo Perfectness". Advances in Computer Games. Lecture Notes in Computer Science. 7168. pp. 258–269.
- Bouzy, B., & Tutorial, C. (2007, April). Old-fashioned computer go vs monte-carlo go (PDF). In IEEE Symposium on Computational Intelligence in Games (CIG).
- Cameron Browne; Edward Powley; Daniel Whitehouse; ... et al. (March 2012). "A Survey of Monte Carlo Tree Search Methods" (PDF). IEEE Transactions on Computational Intelligence and AI in Games. 4 (1): 1–43.
- Chang, Hyeong Soo; Fu, Michael; Hu, Jiaqiao; Marcus, Steven I. (2016). "Google DeepMind's Alphago: O.R.'s unheralded role in the path-breaking achievement". OR/MS Today. 45 (5): 24–29.
- Chaslot, G. M. J., Winands, M. H., Herik, H. J. V. D. ... et al. (2008). Progressive strategies for Monte-Carlo tree search (PDF). New Mathematics and Natural Computation, 4(03), 343-357.
- Guillaume M.J-B. Chaslot, Mark H.M. Winands, Jaap van den Herik (2008). "Parallel Monte-Carlo Tree Search" (PDF). Computers and Games, 6th International Conference, CG 2008, Beijing, China, September 29 – October 1, 2008. Proceedings. H. Jaap van den Herik, Xinhe Xu, Zongmin Ma, Mark H. M. Winands (eds.). Springer. pp. 60–71.
- Markus Enzenberger; Martin Müller (2010). "A Lock-free Multithreaded Monte-Carlo Tree Search Algorithm". In Jaap Van Den Herik; Pieter Spronck (eds.). Advances in Computer Games: 12th International Conference, ACG 2009, Pamplona, Spain, May 11–13, 2009, Revised Papers. Springer. pp. 14–20.
- Richard J. Lorentz (2008). "Amazons Discover Monte-Carlo". Computers and Games, 6th International Conference, CG 2008, Beijing, China, September 29 – October 1, 2008. Proceedings. H. Jaap van den Herik, Xinhe Xu, Zongmin Ma, Mark H. M. Winands (eds.). Springer. pp. 13–24.
- Silver, David; Huang, Aja; Maddison, Chris J.; ... et al. (28 January 2016). "Mastering the game of Go with deep neural networks and tree search (PDF)". Nature. 529 (7587): 484–489.
- Subramanian, K., Scholz, J., Isbell, C. L., & Thomaz, A. L. (2016). Efficient exploration in monte carlo tree search using human action abstractions (PDF). In Proceedings of the 30th International Conference on Neural Information Processing Systems, NIPS (Vol. 16).
- Sylvain Gelly; Yizao Wang; Rémi Munos; Olivier Teytaud (November 2006). Modification of UCT with Patterns in Monte-Carlo Go (PDF). Technical report, INRIA.
拎
[編輯]- (英文) "Lee Sedol defeats AlphaGo in masterful comeback - Game 4". Go Game Guru.














![{\displaystyle [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83021ecdd7307a04dbb7873affcaac031e7e935a)











![{\displaystyle [2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa32363c093f4cfd50ecba68068bcfd396ea8bff)







