搵路

- 一幅表示移動空間嘅圖、
- 起點、以及
- 終點,
然後個演算法就需要計出一條由起點去終點嘅路線(output)[2]。
一個典型嘅搵路演算法通常會同另外兩個特定嘅演算法一齊做嘢:一方面,搵路演算法一般唔能夠直接對要探索嘅環境作出運算,而係要靠另外一個演算法 simp,simp 要以個環境嘅地圖做輸入,將幅地圖抽象化,變成一幅圖論上嘅圖做輸出,等個搵路演算法用呢幅圖做輸入[1];另一方面,因為搵路演算法做嘅只係「搵條路線出嚟」,所以喺搵路演算法行完之後,個程式要將條路線交俾一個教個人工智能移動嘅演算法 follow,等 follow 教部電腦執行「沿條路線移動」呢個動作[3]。
用嚟做搵路嘅演算法有好多實用價值:例如係喺機械人學上教機械人喺自己周圍嘅空間當中搵出要行嘅路線,以及係喺遊戲製作上教遊戲 AI 控制啲 NPC 喺遊戲空間入面搵出要行嘅路線呀噉,都要用到搵路演算法[4][5]。
輸入
[編輯]
一個搵路演算法用起上嚟通常要配以一個將環境轉化成一幅圖嘅演算法:喺實際應用上,搵路演算法通常唔曉直接處理一個環境,而係要靠第個演算法(以下叫 simp)-simp 要將個環境變成一幅圖[歐 1]。一幅圖論[歐 2]定義上嘅「圖」係一個數學結構;一幅噉嘅圖會
喺應用上,一個可能嘅做法係以一柞數字(成一個陣列)表示幅圖,輸入最先嗰個數字代表節點嘅數量,跟住嘅數字表示邊啲節點之間有連結,例:用陣列 [6, 1-2, 1-5, 2-5, 2-3, 5-4, 3-4, 4-6] 表示個圖有 6 個節點,節點 1 同節點 2 之間有連結(可以由節點 1 行去節點 2 或者相反)、節點 1 同節點 5 之間有連結(可以由節點 1 行去節點 5 或者相反)... 如此類推;simp 要做嘅嘢係攞要探索嗰個環境做 input,俾出一個噉嘅陣列做 output 表示個環境當中有邊啲重要位置(節點)同邊啲位置之間有路能夠互通(連結)嘅圖,再將呢個 output 交俾個搵路演算法[6]。
分區做法
[編輯]喺實際應用上,一幅表示環境嘅圖通常會將個環境分拆做數量相對少嘅幾個區域。舉個例說明,想像一隻電子遊戲,隻遊戲嘅虛擬世界係一個 10,000 個單位長、40,000 個單位闊嘅四方形,有成 10,000 × 40,000 咁多個可能位置,而如果部電腦要計晒咁多個可能位置會好吃力;不過呢個虛擬世界可以分割做六大區域,而每個區域下又有得細分,於是個遊戲程式可以用一個分層式嘅做法,先睇吓要郁嗰個個體要由邊個區去邊個區,然後忽略唔使考慮嗰啲區域-運算起上嚟就輕鬆好多[7]。

權重表
[編輯]電子遊戲用嘅搵路演算法通常仲會有一個權重表[歐 4],意思即係話個表每條連結都會有個數值[註 1],表示嗰條路線嘅成本[歐 5][8]:例如有個負責整一幅圖嘅演算法會每條路俾個權重值佢,個數值愈大表示條路愈難行(成本高);想像其中兩個節點之間有兩條可能路線 a 同 b,a 係一條完全冇機關嘅平路,而 b 長過 a 之餘仲有十個陷阱設咗喺度,噉正路嚟講,假設 a 同 b 喺其他因素上完全相等,b 嘅權重值理應會大過 a 嘅[9]。
順帶一提,喺電子遊戲嘅搵路當中,仲有好多變數能夠影響搵路嘅權重。例如一個 AI 角色本身嘅特性亦都可能會影響佢嘅搵路權重:想像有隻戰略遊戲,玩家旗下嘅軍隊有兩種單位-步兵同偵察兵,當中偵察兵有特殊能力,令佢哋行起崎嶇不平嘅路嗰陣快啲。噉對於由 AI 控制嘅偵察兵嚟講,「條路嘅平坦程度」對佢哋路線權重嘅影響理應會冇咁大[1]。
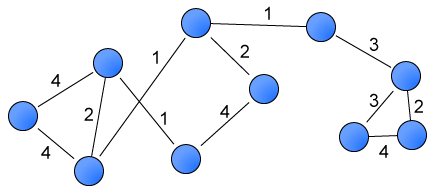
A* 搜尋
[編輯]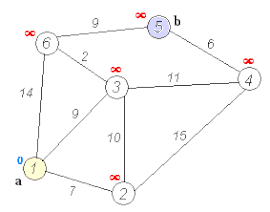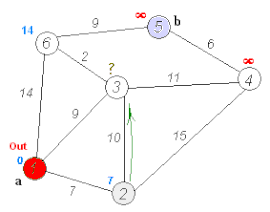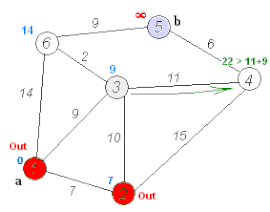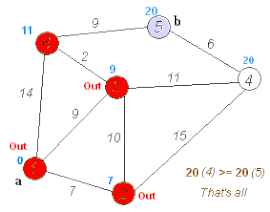
A* 搜尋演算法[歐 6]係最原始嗰種搵路演算法,喺廿世紀同廿一世紀初成日俾人用嚟教電子遊戲人工智能控制 NPC 喺遊戲世界入面移動:一隻電子遊戲嘅虛擬世界可以想像成一個二維嘅平面,個平面會有若干個可以去嘅地點,地點之間有路線,而因為遊戲世界會有障礙物,某啲地點之間嘅空間會唔能夠通行[10]。A* 搜尋演算法嘅做法係將個空間當做一幅有若干個節點嘅圖,喺每一步,個演算法會
- Foreach 相鄰點(可以由自己位置移去嘅地點)計嗰個相鄰點嘅 值; 表示成本(即係行去嗰點要嘥幾多時間精神等資源),數值係 同 嘅總和;
- 表示由現時點去嗰個相鄰點要用嘅移動成本(時間同氣力等),呢個數值可以由現時點同目標點之間嘅路線嘅特性(有幾崎嶇等)估計;
- 係按某啲啟發法[歐 7]估計嘅「由嗰個相鄰點去最終點嘅成本」-例如如果終點喺山頂,而望緊嗰個相鄰點位置低過現時點,按「盡可能喺高度上接近最終點」嘅啟發法,望緊嗰個相鄰點就會有高嘅 值;
然後個演算法會揀 值最低嗰點做下一個要去嘅點,唔好去經已去過嘅點,並且一路重複做上述嘅嘢,順利嘅話就會一路做到到達終點為止[10][11]。A* 搜尋演算法仲可以狹義化,變成迪卡斯特拉演算法[歐 8]:迪卡斯特拉演算法係指 永遠等如 0 嘅 A* 搜尋演算法,即係話迪卡斯特拉演算法唔會嘗試估下一點有幾有利於最後去到終點[12][13]。
初始化 個程式有兩個 list,開放表(open list)同封閉表(closed list); // 開放表表示未去過嘅點,而封閉表表示去咗嘅點。 將起點擺入去 open list; While open list 唔係空嘅,做... 搵 open list 當中 f 值最低嘅點; 將呢點變做現時點; 將呢點擺入去 closed list; // 等個程式唔會返去經已去過嘅點。 Foreach 由現時點去得到嘅點, if 嗰點喺 closed list 入面,忽略佢; if 呢點唔喺 open list 入面,將佢擺入去 open list; 將現時點設做呢點嘅 parent; 計呢點嘅 f 值; if 最終目的地入咗 closed list,終止運作; // 成功到咗目的地。 if open list 係空嘅,但又搵唔到目的地嗰點,終止運作; // 搵路失敗。 將個演算法行過嗰條路線俾做 output。
呢個演算法嘅最壞情況複雜度係 O(E),當中 E 係幅圖嘅節點間連結嘅數量[14]。
計 h
[編輯]
A* 同迪卡斯特拉演算法嘅分別在於 A* 會考慮 呢個數值。原則上, 可以用兩大方法計[14]:
- 個演算法可以試吓計 嘅精確數值,即係例如考慮晒所有由目標點去終點嘅可能路線,再計出 嘅最細可能數值;呢種做法有個明顯嘅缺點-噉做會消耗大量嘅運算資源,而且仲假設咗個演算法有能力鳥瞰噉睇晒成幅地圖同埋事先知道晒每條路線嘅成本值[註 3][15]。所以
- 喺實際應用上, 嘅數值通常會用某啲啟發法估計:啟發法係認知心理學上嘅一個概念,指人類或者人工智能思考嗰陣可以用嘅「認知捷徑」,即係一啲簡單(唔使做太大量嘅運算)、可以用嚟解難嘅法則,例如家陣個搵路演算法要由喺山腳嘅起點行去喺山頂嘅終點,一個可能嘅啟發法就可以係「盡可能行去高嘅點」( 嘅數值同望緊嗰點嘅高度成反比)。A* 演算法有多種啟發法可以用嚟估計 嘅數值,多數係靠計終點同望緊嗰點之間嘅距離,而「距離」嘅計法有幾種[16]:
- 曼哈頓距離[歐 9]:想像兩個點之間嘅空間用格仔嚟代表,而假設一個個體淨係有得沿住啲格仔嘅邊線行(好似係一個喺曼哈頓揸車搵食嘅的士司機噉)嘅話,噉喺是但兩點(設呢兩點做 同 )之間穿梭都會有多條「最短路線」,呢啲路線嘅長度就係所謂嘅曼哈頓距離。喺二維空間嘅情況下,曼哈頓距離計法如下[17]:
- ;當中 係指 嘅 座標值、 係指 嘅 座標值... 如此類推。
- 棋盤距離[歐 10]:指兩點之間最大座標差異,兩點之間嘅棋盤距離係指將兩點嘅同位座標相減(兩點嘅 座標相減、兩點嘅 座標相減... 等等)所得嘅最大數值,條式如下[18]:
- 歐幾里得距離[歐 11]:指兩點之間嘅直線距離,二維嘅歐幾里得距離計法如下[16]:
- 曼哈頓距離[歐 9]:想像兩個點之間嘅空間用格仔嚟代表,而假設一個個體淨係有得沿住啲格仔嘅邊線行(好似係一個喺曼哈頓揸車搵食嘅的士司機噉)嘅話,噉喺是但兩點(設呢兩點做 同 )之間穿梭都會有多條「最短路線」,呢啲路線嘅長度就係所謂嘅曼哈頓距離。喺二維空間嘅情況下,曼哈頓距離計法如下[17]:
任何角度
[編輯]Theta* 係一個進階版嘅 A* 搜尋演算法,特徵係曉靠自己檢查現時位置周圍嘅點(睇埋任何角度路線計劃):Theta* 嘅主要過程同 A* 一樣,不過喺每次睇周圍節點嗰陣,唔淨只會睇同現時點 有連繫嘅節點,而係睇晒所有由 望得到嘅點,而如果有個點 係由 望得到嘅,噉個演算法有可能會選擇由 直接移去 -就算 同 之間冇直接嘅連繫都一樣。即係話[19]:
... // 其餘部份同一般嘅 A* 一樣。 Foreach 由現時點去得到嘅點, if 嗰點喺 closed list 入面,忽略佢; if 呢點唔喺 open list 入面,將佢擺入去 open list; Update vertex // 呢個子程序係 theta* 同 A* 嘅分別;簡單講係睇勻周圍嘅望得到嘅點,揀成本最低嗰個,然後再由現時點直接畫條路去嗰度。 將現時點設做呢點嘅 parent; 計呢點嘅 f 值; ...
進階技術
[編輯]幅度同深度
[編輯]幅度優先搜尋[歐 12]同深度優先搜尋[歐 13]係搜尋演算法上兩個相關嘅概念。幅度優先搜尋係先入先出[歐 14]嘅,喺開始做搜尋嗰陣,會睇晒所有「下一個可能去嘅點」先,然後再睇下一列可能地點-「以幅度廣為先」;深度優先搜尋就係用後入先出[歐 15]嘅,會先攞一個點,然後集中睇嗰點之後嘅可能點-「以深度高為先」。對搵路嘅演算法研究會思考「幅度優先同深度優先分別擅長喺邊啲情況下搵出總成本低嘅路線」,並且按情況揀啱用啲嗰種做法[20][21]。
喺實用上,幅度優先搜尋同深度優先搜尋嘅演算法都會有某啲可調節嘅參數:例如一個深度優先搜尋嘅演算法通常會掕住個數值 ,表示「搜尋深度」,例如 就表示「喺
多個體搵路
[編輯]多個體搵路演算法[歐 16]係指幫多個個體喺一個環境入面搵出每一個個體要行嘅路線,同時確保啲個體之間唔會相撞同埋將成本函數最佳化(將成本減到最低)-成本可以用(例如)「個體嘅路線長度總和」嚟衡量;多個體搵路要應付「要用嘅運算資源隨個體數量激增」等嘅問題[23]。
喺現實應用上,多個體搵路演算法通常會將啲個體分做若干組-例如一隻射擊遊戲,由電腦控制嘅敵軍有 24 個士兵,而呢柞士兵可以分做 6 個小隊,一個小隊嘅成員會群體同步移動,即係用同一條路線,令到個搵路過程由「搵 24 條路」變成(消耗嘅運算資源比較少嘅)「搵 6 條路」,然後再有進一步嘅演算法,教每個體要同條路線成點嘅關係,例如小隊有個隱形(玩家睇唔到)嘅中心點,而每個士兵喺個小隊移動嗰陣,要確保自己一路都喺小隊中心點嘅 -10 + (x * 5) 咁遠嘅位置,當中 x 係佢係小隊入面第幾個士兵[24][25]。
文獻
[編輯]- Abd Algfoor, Z., Sunar, M. S., & Kolivand, H. (2015). A comprehensive study on pathfinding techniques for robotics and video games (PDF). International Journal of Computer Games Technology, 11 pages.
- S. Koenig & M. Likhache. Incremental A* (PDF).
- S. Koenig & M. Likhache (2002). D* Lite (PDF).
註釋
[編輯]歐詞
[編輯]睇埋
[編輯]攷
[編輯]- ↑ 1.0 1.1 1.2 1.3 Millington, I. (2019). AI for Games. CRC Press. Ch. 4.
- ↑ Hagelback, Johan, and Stefan J. Johansson. "Dealing with fog of war in a real-time strategy game environment." In Computational Intelligence and Games, 2008. CIG'08. IEEE Symposium On, pp. 55-62. IEEE, 2008.
- ↑ Millington, I. (2019). AI for Games. CRC Press. p. 82.
- ↑ Cui, X., & Shi, H. (2011). A*-based pathfinding in modern computer games. International Journal of Computer Science and Network Security, 11(1), 125-130.
- ↑ Boyarski, E., Felner, A., Stern, R., Sharon, G., Tolpin, D., Betzalel, O., & Shimony, E. (2015, June). ICBS: improved conflict-based search algorithm for multi-agent pathfinding. In Twenty-Fourth International Joint Conference on Artificial Intelligence.
- ↑ Pathfinding Algorithms. Medium.
- ↑ Botea, Adi and Muller, Martin and Schaeffer, Jonathan (2004). "Near optimal hierarchical path-finding". Journal of Game Development. 1: 7–28.
- ↑ Fletcher, Peter; Hoyle, Hughes; Patty, C. Wayne (1991). Foundations of Discrete Mathematics (International student ed.). Boston: PWS-KENT Pub. Co. p. 463. ISBN 978-0-53492-373-0. "A weighted graph is a graph in which a number w(e), called its weight, is assigned to each edge e."
- ↑ Antsfeld, L., Harabor, D. D., Kilby, P., & Walsh, T. (2012, October). Transit routing on video game maps. In Eighth Artificial Intelligence and Interactive Digital Entertainment Conference.
- ↑ 10.0 10.1 10.2 Zeng, W.; Church, R. L. (2009). "Finding shortest paths on real road networks: the case for A*". International Journal of Geographical Information Science. 23 (4): 531–543.
- ↑ Barnouti, N. H., Al-Dabbagh, S. S. M., & Naser, M. A. S. (2016). Pathfinding in strategy games and maze solving using A* search algorithm. Journal of Computer and Communications, 4(11), 15.
- ↑ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Section 24.3: Dijkstra's algorithm". Introduction to Algorithms (Second ed.). MIT Press and McGraw–Hill. pp. 595–601.
- ↑ Knuth, D. E. (1977). "A Generalization of Dijkstra's Algorithm". Information Processing Letters. 6 (1): 1–5.
- ↑ 14.0 14.1 14.2 A* Search Algorithm. GeeksforGeeks.
- ↑ Delling, D.; Sanders, P.; Schultes, D.; Wagner, D. (2009). "Engineering route planning algorithms". Algorithmics of Large and Complex Networks: Design, Analysis, and Simulation. Lecture Notes in Computer Science. 5515. Springer. pp. 117–139.
- ↑ 16.0 16.1 Euclidean vs Manhattan vs Chebyshev Distance.
- ↑ Black, Paul E. "Manhattan distance". Dictionary of Algorithms and Data Structures.
- ↑ Cyrus. D. Cantrell (2000). Modern Mathematical Methods for Physicists and Engineers. Cambridge University Press.
- ↑ Daniel, K.; Nash, A.; Koenig, S.; Felner, A. (2010). "Theta*: Any-Angle Path Planning on Grids 互聯網檔案館嘅歸檔,歸檔日期2021年4月11號,." (PDF). Journal of Artificial Intelligence Research. 39: 533–579.
- ↑ 20.0 20.1 Breadth First Search and Depth First Search. Medium.
- ↑ Cormen, Thomas H. "22.2 Breadth-first search". Introduction to algorithms.
- ↑ Smart Move: Intelligent Path-Finding. Gamasutra.
- ↑ Ma, H., Koenig, S., Ayanian, N., Cohen, L., Hönig, W., Kumar, T. K., ... & Sharon, G. (2017). Overview: Generalizations of multi-agent path finding to real-world scenarios 互聯網檔案館嘅歸檔,歸檔日期2021年7月15號,. (PDF). arXiv preprint arXiv:1702.05515.
- ↑ Ma, H., & Koenig, S. (2016). Optimal target assignment and path finding for teams of agents. arXiv preprint arXiv:1612.05693.
- ↑ Stern, R., Sturtevant, N., Felner, A., Koenig, S., Ma, H., Walker, T., ... & Boyarski, E. (2019). Multi-agent pathfinding: Definitions, variants, and benchmarks (PDF). arXiv preprint arXiv:1906.08291.
拎
[編輯]- Clear visual A* explanation, with advice and thoughts on path-finding (英文)
- Variation on A* called Hierarchical Path-Finding A* (HPA*) (英文)
- Difference between BFS and DFS, GeeksForGeeks (英文)
- Smart Move: Intelligent Path-Finding, Gamasutra (英文)






















