譜聚類

有兩隻連通元件嘅圖

譜聚類（英文：Spectral clustering）係一種聚類分析方法，要聚類嘅對象着視為一幅圖啲綟，啲對象之間嘅距離或者嘸相似度係着表示成圖啲綟之間啲加有權嘅檠。譜聚類係基於圖論對於個拉氏矩陣嘅分析結果，個拉氏矩陣對應返啲圖係有$k$隻連通元件。由於矩陣啲特徵值亦都喊做頻譜，所以種方法喊做譜聚類。譜聚類嘅圖論理論基礎係由 Donath & Hoffman (1973) 同 Fiedler (1973) 奠定嘅。

數學基礎

圖縮減

喺第一步，個圖着縮減，而個目的係從圖裏便鏟走所有啲權重（象徵距離）太大嘅檠。以下係啲方法：

ε鄰舍圖

若果某檠嘅權重大過$\epsilon$，就由圖度鏟走條檠。

k-nn 圖

喺 k-nn 圖（$k$最近鄰舍圖）裏便，一粒綟啲所有檠都根據檠嘅權重排序。有檠個權重大過第$k$個最細權重嘅（象徵遠過第$k$個鄰舍），就着從圖度鏟走。個$k$ -nn 係嘸對稱嘅，即隻檠權重$w_{ij}$可能對於$o_{i}$嚟講係細過第$k$個最細檠權重，之對於$o_{j}$又嘸細過佢個第$k$個最細檠權重。得喊做係 k-nn 圖只需要到條檠保留喺圖裏便嘅，對於$o_{i}$或者$o_{j}$其中至少一個對象，個$w_{ij}$細過佢第$k$個最細檠權重，即係每個對象至少有$k$條檠。相反，一個「 佮埋嘅 k-nn 圖」只包含有啲檠、啲對於兩個對象都有$w_{ij}$細過$k$個最細檠權重嘅，即係每個對象都最多有$k$條檠。

全連接圖

藉助相似度函數，檠權重係根據對象之間啲距離計出。相似度函數嘅一個例係高斯相似度函數$s(o_{i},o_{j})=\exp(-{\tfrac {1}{2}}d^{2}(o_{i},o_{j})/\sigma ^{2})$。參數$\sigma$控制鄰舍大細似上高個參數$\epsilon$或者$k$噉。

• 
  二維空間裏便8個對象嘅位置。
• 
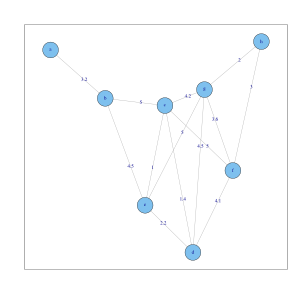
  全連接圖，有啲帶歐氏距離嘅檠褦住8個對象。
• 
  8個對象啲歐氏距離嘅距離矩陣。
• 
  $\epsilon$鄰舍圖（ $\epsilon =5$） 為8個對象。
• 
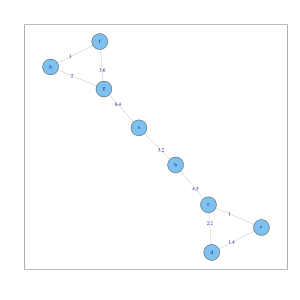
  8個對象個k-nn 圖（$k=2$） 。每粒綟至少有兩條檠。
• 
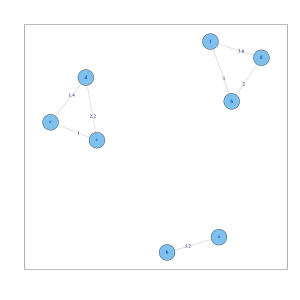
  8個對象個普通 k-nn圖（ $k=2$）。每粒綟最多有兩條檠。數據集着分成三隻連通元件。
• 
  拉氏矩陣$L_{rw}$，對於8個對象個普通 k-nn 圖（$k=2$） 嘅。
• 
  全連接圖，有返啲檠有高斯相似度函數值（$\sigma =3$），表示到8個對象。

拉氏矩陣

透過檠權重可以幫$n$個對象整出（加權）鄰接矩陣$W$。次數矩陣$D$入便，對角線上包含有通向綟啲檠嘅權重總和（喺圖縮減之後）。係噉計得出三種拉氏矩陣：

• 非歸一化矩陣$L=D-W$ ,
• 歸一化矩陣$L_{sym}=D^{-1/2}LD^{-1/2}$
• 歸一化矩陣$L_{rw}=D^{-1}L$ .

對於所有啲向量$f\in R^{n}$有：

${\begin{array}{rcll}f^{T}Lf&=&\displaystyle {\tfrac {1}{2}}\sum _{i,j=1}^{n}w_{ij}\left(f_{i}-f_{j}\right)^{2}&\geq 0,\\f^{T}L_{sym}f&=&\displaystyle {\tfrac {1}{2}}\sum _{i,j=1}^{n}w_{ij}\left({\tfrac {f_{i}}{\sqrt {d_{i}}}}-{\tfrac {f_{j}}{\sqrt {d_{j}}}}\right)^{2}&\geq 0.\\f^{T}L_{rw}f&=&\displaystyle {\tfrac {1}{2}}\sum _{i,j=1}^{n}w_{ij}\left(f_{i}-f_{j}\right)^{2}&\geq 0\\\end{array}}$

由於拉氏矩陣係對稱同埋半正定嘅，所有特徵值都係實值而且大於或者等於零。對於拉氏矩陣，可以證明至少有一個特徵值係零。若果個圖由$k$隻連通元件整出，係噉拉氏矩陣就係一個壆矩陣（Block矩陣，見上高幅圖同埋矩陣）。每一壆都有一個等於零嘅特徵值。對於特徵值係零嘅特徵向量必須有$f^{T}Lf=0$。因爲所有啲檠權重$w_{ij}$係正嘅，一隻連通元件啲綟所有$f_{i}$都必須相同（所以有$f_{i}-f_{j}=0$）。對於$L_{sym}$都有類似分析，唯有係特徵向量入便啲欄係由$d_{i}$加權，而對於$L_{rw}$特徵向量啲欄$f_{i}$係等於1。

對於聚類，分析拉氏矩陣啲最細特徵值同埋特徵向量。

• 
  普通k-nn圖個拉普拉斯矩陣啲特徵值（ $k=3$），對於個8個對象嘅數據。由於該圖由三隻連通元件組成，所以存在有三個值為0嘅特徵值。
• 
  三枚特徵向量啲值、拉氏矩陣$L_{rw}$啲特徵值係零嘅。啲欄應該等於 1，但個軟件重新調整過啲特徵向量，令佢哋長度係 1（即表中分別係$-1/{\sqrt {3}}$、$1/{\sqrt {2}}$、$1/{\sqrt {3}}$，等啲特徵向量自點乘會得出1）。
• 
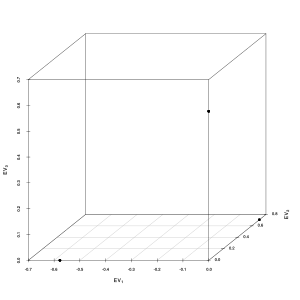
  3D 散點圖畀特徵值零嘅三枚特徵向量嘅。8個對象着重疊畫喺三笪埞（overplotting），等 k平均聚類可以完美噉搵得到三隻連通元件。

演算法

各式演算法

嘸同嘅譜聚類演算法有着開發出嚟：

非歸一化譜聚類：

1. 計非歸一化嘅拉氏矩陣$L$
2. 計前$k$枚特徵向量（係有$k$最細特徵值嘅）
3. 攞$k$枚特徵向量啲行並用分匹方法整聚類，譬如k-平均演算法

Shi佮Malik嘅歸一化譜聚類：

1. 計歸一化嘅拉氏矩陣$L_{rw}$
2. 計前$k$特徵向量（係有$k$最細特徵值嘅）
3. 攞$k$枚特徵向量啲行並用分匹方法整聚類

Ng、Jordan佮Weiss嘅歸一化譜聚類 ：

1. 計歸一化嘅拉氏矩陣$L_{sym}$
2. 計前$k$特徵向量（係有$k$最細特徵值嘅）
3. 攞$k$枚特徵向量啲行並用分匹方法整聚類

參數揀選

關於過程參數同演算法嘅揀選，Ulrike von Luxburg個教程推薦係：

• 鄰舍圖嘅揀選：k-nn 圖，因為識別嘸同密度嘅聚類識別得好啲並生成得稀疏拉氏矩陣。$k$亦都可以喺大啲嘅域內變化，而同時嘸會改變到個聚類分析好多。
• 鄰舍圖啲參數嘅揀選：
  • 對於k-nn 圖，$k$係噉揀選嘅，即個圖啲連通元件嘸少過預期聚類裏便應有嘅。
  • 對於普通 k-nn 圖，$k$要大過k-nn度嘅，因爲普通k-nn 圖包含到嘅檠少過k-nn 圖。揀選$k$嘅啟發式方法仲未知。
  • 對於$\epsilon$鄰舍圖應該揀$\epsilon$係等於最長條檠喺最細生成樹（minimum spanning tree）度嘅。
  • 對於啲全連接圖有高斯相似度函數嘅應該揀$\sigma$係令到結果幅圖對應返 k-nn 圖或者$\epsilon$鄰舍圖。經驗法則仲有：$\sigma$等於最長條檠喺最細生成樹嘅或者$\sigma$作爲個平均距離去到$k$隻最近鄰舍嘅，其中$k=1+\log(n)$ .
• 聚類數嘅揀選：畫出拉氏矩陣啲特徵值，照大細排序並搵跳躍，譬如喺上高示意圖入便8對象數據集個第3同第4特徵值之間嘅。
• 拉氏矩陣嘅揀選：因爲對於$L_{rw}$嚟講，特徵向量入便啲欄係等於1，攞譬如k-means 演算法嚟聚類會幾好。

例

Iris花數據集，係Sir Ronald Fisher爵士 (1936) 作爲判別分析嘅例使用到嘅。有時，個數據集亦都着喊做「Anderson's Iris花數據集」，因為Edgar Anderson收集唨啲數據嚟量化Iris花嘅形態變化。個數據集由 50 隻標本組成，每隻標本分為三隻物種：Iris setosa、Iris versicolor、Iris virginica。分別有測量到萼片同花瓣嘅長度同埋寬度，所以個數據集包含有150個觀察值同埋4個變量。

• 
  Iris花數據集啲散佈圖矩陣，數據點啲色對應於三種類型。
• 
  Iris花數據集裏便歐氏距離嘅熱圖。色愈深，對象之間啲距離愈細。
• 
  Iris 數據集上嘅譜聚類結果。

就好似喺散佈圖矩陣個左便（第一幅）圖形見到噉，三種類型之一（圖形中啲紅色）戥其他類型顯著嘸同。另外兩個物種互相之間好難分開。中間（第二幅）圖形顯示對象之間啲歐氏距離嘅灰度熱圖。灰色越深，對象離得越近。呢啲對象經已係噉重新排列法，即戥其他對象有相似距離嘅對象互相之間擺近。使用到嘅軟件用層次聚類嘅方法並顯示到個樹狀結構圖（Dendrogram）。右便（第三幅）圖形顯示到譜聚類嘅結果。可以睇得出，啲聚類戥三種類型有一定嘅一致性。

• 
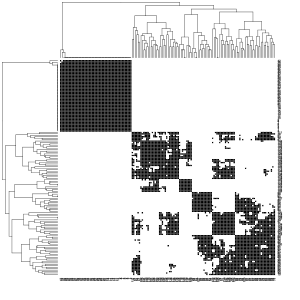
  黑色：啲對象之間嘅檠，喺 k-nn 圖（ $k=50$ ）度保有。白色：啲捱鏟走嘅檠。
• 
  黑色：啲對象之間嘅檠，喺普通 k-nn 圖（ $k=50$ ）度保有。白色：啲捱鏟走嘅檠。
• 
  散佈圖畀拉氏矩陣$L_{rw}$啲特徵值，對於k-nn 圖（$k=50$ ）。

左便兩幅圖像顯示到k-nn 圖或者普通 k-nn 圖裏便係邊啲檠着保留到（黑色）或者嘸着保留到（白色）。對於參數$k$，最長檠首先係喺最細生成樹中着確定到，然之後幫所有觀察值計出對應嘅鄰舍數。平均值大概係 60 個鄰舍，係噉揀$k=50$。之後計拉氏矩陣$L_{rw}$同埋矩陣啲特徵值。特徵值圖顯示到喺第二個或者第三個特徵值之後有好大跳躍。然之後對前三枚特徵向量進行3聚類嘅 k平均聚類。

種	聚類結果
	1	2	3
setosa	0	0	50
versicolor	43	7	0
virginica	7	43	0

個混淆矩陣表明到譜聚類喺某種程度上重新發現過啲物種。譜聚類法完全正確噉分出Setosa聚類；喺 Versicolor同Virginica聚類嘅情況下有7 個觀測值各自捱錯誤噉分類到，對應嘅錯誤分類率係$14/150\approx 9{,}4\,\%$。