向量代數公式

以下係向量代數入面嘅常見公式。公式只牽涉向量嘅長度$\|\mathbf {A} \|$同埋內積$\mathbf {A} \cdot \mathbf {B}$嘅話，就喺所有嘅維度都啱。如果條公式有叉積$\mathbf {A} \times \mathbf {B}$嘅話，就只可以用喺三維。（雖然七維都有個積叫叉積，但係下邊嘅公式喺七維未必啱。）

記號嚟講，喺n維歐幾量得空間入邊，每支向量都可以用佢喺各個方向嘅分量（component）嚟表示：$\mathbf {A} =(A_{1},A_{2},\ldots ,A_{n})$，如果喺三維嘅話，可以用$x,y,z$代替：$\mathbf {A} =(A_{x},A_{y},A_{z})$。

長度

根據定義，一支向量$\mathbf {A}$嘅長度係佢同佢自己內積嘅開方：

$\|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }}$

$\|\mathbf {A} \|^{2}=\mathbf {A} \cdot \mathbf {A}$

用座標嚟寫嘅話，就有：

$\|\mathbf {A} \|={\sqrt {A_{1}^{2}+A_{2}^{2}+A_{3}^{2}+\ldots +A_{n}^{2}}}$

$\|\mathbf {A} \|^{2}=A_{1}^{2}+A_{2}^{2}+A_{3}^{2}+\ldots +A_{n}^{2}=\sum _{i=1}^{n}A_{i}^{2}$

即係勾股定理。

不等式

• 柯西不等式：$\mathbf {A} \cdot \mathbf {B} \leq \|\mathbf {A} \|\|\mathbf {B} \|$
• 三角不等式：$\|\mathbf {A} +\mathbf {B} \|\leq \|\mathbf {A} \|+\|\mathbf {B} \|$
• 反三角不等式：$\|\mathbf {A} -\mathbf {B} \|\geq {\Big \vert }\|\mathbf {A} \|-\|\mathbf {B} \|{\Big \vert }$

角度

用$\theta$嚟表示向量$\mathbf {A}$同$\mathbf {B}$之間嘅夾角嘅話，有：

$\sin \theta ={\frac {\|\mathbf {A} \times \mathbf {B} \|}{\left\|\mathbf {A} \right\|\left\|\mathbf {B} \right\|}}\quad (-\pi <\theta \leq \pi )$

$\cos \theta ={\frac {\mathbf {A} \cdot \mathbf {B} }{\left\|\mathbf {A} \right\|\left\|\mathbf {B} \right\|}}\quad (-\pi <\theta \leq \pi )$

結合以上兩條式同埋畢達哥拉斯三角等式嘅話，就有：

$\left\|\mathbf {A\times B} \right\|^{2}+(\mathbf {A} \cdot \mathbf {B} )^{2}=\left\|\mathbf {A} \right\|^{2}\left\|\mathbf {B} \right\|^{2}$

如果一支向量$\mathbf {A}$同正交軸$x_{i}$-軸嘅夾角分別係$\theta _{i}$嘅話，咁：

$\cos \theta _{i}={\frac {A_{i}}{\sqrt {A_{1}^{2}+A_{2}^{2}+\ldots +A_{n}^{2}}}}={\frac {A_{i}}{\|\mathbf {A} \|}}$

夾埋嗮一齊：

$\mathbf {A} =\|\mathbf {A} \|\left(\cos \theta _{1}{\hat {\mathbf {x} _{i}}}+\ldots +\cos \theta _{n}{\hat {\mathbf {x} _{n}}}\right)$

其中${\hat {\mathbf {x} _{i}}}$係$x_{i}$軸上面嘅單位向量。

面積同體積

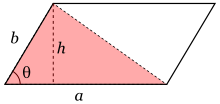鄰邊長度係a、b，夾角係$\theta$。

一個平行四邊形，一對鄰邊長度係a、b且夾角係$\theta$嘅話（右圖），佢嘅面積$\Sigma$就係：

$\Sigma =ab\sin \theta ,$

可以諗做三維空間入面向量$\mathbf {A}$、$\mathbf {B}$叉積嘅長度：

$\Sigma =\left\|\mathbf {A} \times \mathbf {B} \right\|={\sqrt {\left\|\mathbf {A} \right\|^{2}\left\|\mathbf {B} \right\|^{2}-\left(\mathbf {A} \cdot \mathbf {B} \right)^{2}}}$

呢條式嘅平方係：

$\Sigma ^{2}=(\mathbf {A\cdot A} )(\mathbf {B\cdot B} )-(\mathbf {A\cdot B} )(\mathbf {B\cdot A} )=\Gamma (\mathbf {A} ,\ \mathbf {B} )\ ,$

呢到 Γ(A, B) 係 A同B嘅Gram 判別式：

$\Gamma (\mathbf {A} ,\ \mathbf {B} )={\begin{vmatrix}\mathbf {A\cdot A} &\mathbf {A\cdot B} \\\mathbf {B\cdot A} &\mathbf {B\cdot B} \end{vmatrix}}$

同樣，三支向量$\mathbf {A} ,\mathbf {B} ,\mathbf {C}$生成嘅平行六面體嘅體積可以用三支向量嘅 Gram 判別式嚟計：

$V^{2}=\Gamma (\mathbf {A} ,\ \mathbf {B} ,\ \mathbf {C} )={\begin{vmatrix}\mathbf {A\cdot A} &\mathbf {A\cdot B} &\mathbf {A\cdot C} \\\mathbf {B\cdot A} &\mathbf {B\cdot B} &\mathbf {B\cdot C} \\\mathbf {C\cdot A} &\mathbf {C\cdot B} &\mathbf {C\cdot C} \end{vmatrix}}\ ,$

因爲$\mathbf {A} ,\mathbf {B} ,\mathbf {C}$都係三維向量，呢個數又等於佢哋嘅純量三重積：$\det[\mathbf {A} ,\mathbf {B} ,\mathbf {C} ]=|\mathbf {A} ,\mathbf {B} ,\mathbf {C} |$ （睇埋下邊）。

同樣嘅計法可以推廣去 n 維空間。

加法同乘法

• 加法交換律：$\mathbf {A} +\mathbf {B} =\mathbf {B} +\mathbf {A}$.
• 內積交換律：$\mathbf {A} \cdot \mathbf {B} =\mathbf {B} \cdot \mathbf {A}$.
• 叉積反交換律：$\mathbf {A} \times \mathbf {B} =\mathbf {-B} \times \mathbf {A}$.
• 純量乘法對加法嘅分配律：$c(\mathbf {A} +\mathbf {B} )=c\mathbf {A} +c\mathbf {B}$.
• 內積對加法嘅分配律：$\left(\mathbf {A} +\mathbf {B} \right)\cdot \mathbf {C} =\mathbf {A} \cdot \mathbf {C} +\mathbf {B} \cdot \mathbf {C}$.
• 叉積對加法嘅分配律：$(\mathbf {A} +\mathbf {B} )\times \mathbf {C} =\mathbf {A} \times \mathbf {C} +\mathbf {B} \times \mathbf {C}$.
• 純量三重積：$\mathbf {A} \cdot (\mathbf {B} \times \mathbf {C} )=\mathbf {B} \cdot (\mathbf {C} \times \mathbf {A} )=\mathbf {C} \cdot (\mathbf {A} \times \mathbf {B} )$$=|\mathbf {A} \,\mathbf {B} \,\mathbf {C} |={\begin{vmatrix}A_{x}&B_{x}&C_{x}\\A_{y}&B_{y}&C_{y}\\A_{z}&B_{z}&C_{z}\end{vmatrix}}$.
• 向量三重積：$\mathbf {A} \times (\mathbf {B} \times \mathbf {C} )=(\mathbf {A} \cdot \mathbf {C} )\mathbf {B} -(\mathbf {A} \cdot \mathbf {B} )\mathbf {C}$.
• Jacobi 等式：$\mathbf {A} \times (\mathbf {B} \times \mathbf {C} )+\mathbf {C} \times (\mathbf {A} \times \mathbf {B} )+\mathbf {B} \times (\mathbf {C} \times \mathbf {A} )=\mathbf {0}$.
• Binet-Cauchy 等式：$\mathbf {\left(A\times B\right)\cdot } \left(\mathbf {C} \times \mathbf {D} \right)=\left(\mathbf {A} \cdot \mathbf {C} \right)\left(\mathbf {B} \cdot \mathbf {D} \right)-\left(\mathbf {B} \cdot \mathbf {C} \right)\left(\mathbf {A} \cdot \mathbf {D} \right)$.
• Lagrange 等式：$|\mathbf {A} \times \mathbf {B} |^{2}=(\mathbf {A} \cdot \mathbf {A} )(\mathbf {B} \cdot \mathbf {B} )-(\mathbf {A} \cdot \mathbf {B} )^{2}$.
• 向量四重積： $(\mathbf {A} \times \mathbf {B} )\times (\mathbf {C} \times \mathbf {D} )\ =\ |\mathbf {A} \,\mathbf {B} \,\mathbf {D} |\,\mathbf {C} \,-\,|\mathbf {A} \,\mathbf {B} \,\mathbf {C} |\,\mathbf {D} \ =\ |\mathbf {A} \,\mathbf {C} \,\mathbf {D} |\,\mathbf {B} \,-\,|\mathbf {B} \,\mathbf {C} \,\mathbf {D} |\,\mathbf {A}$.
• 上式嘅一個推論 $|\mathbf {A} \,\mathbf {B} \,\mathbf {C} |\,\mathbf {D} =(\mathbf {A} \cdot \mathbf {D} )\left(\mathbf {B} \times \mathbf {C} \right)+\left(\mathbf {B} \cdot \mathbf {D} \right)\left(\mathbf {C} \times \mathbf {A} \right)+\left(\mathbf {C} \cdot \mathbf {D} \right)\left(\mathbf {A} \times \mathbf {B} \right)$.
• 三維入邊嘅向量$\mathbf {D}$用（唔一定正交嘅）基底$\{\mathbf {A} ,\mathbf {B} ,\mathbf {C} \}$寫出嚟：
  $$\mathbf {D} \ =\ {\frac {\mathbf {D} \cdot (\mathbf {B} \times \mathbf {C} )}{|\mathbf {A} \,\mathbf {B} \,\mathbf {C} |}}\ \mathbf {A} +{\frac {\mathbf {D} \cdot (\mathbf {C} \times \mathbf {A} )}{|\mathbf {A} \,\mathbf {B} \,\mathbf {C} |}}\ \mathbf {B} +{\frac {\mathbf {D} \cdot (\mathbf {A} \times \mathbf {B} )}{|\mathbf {A} \,\mathbf {B} \,\mathbf {C} |}}\ \mathbf {C} .$$

睇埋

• 向量空間

• 向量
• 內積
• 叉積

• 幾何代數