急變率
| 急變率 | |
|---|---|
 位置嘅時間導數,包括急變率 | |
Common symbols | j、j, Template:Vec |
| In [[SI base unit|Template:Allow wrap]] | m·s-3,m/s3 |
| Dimension | L T−3 |
急變率(又叫突變)係指物體加速度隨時間變化嘅速率。佢係一個向量量(即係有大小同方向)。急變率最常見用符號 j 表示,單位係 m/s3(國際單位制)或者每秒標準重力(g0/s)。
生理影響同人類感知
[編輯]人體嘅姿勢係靠平衡拮抗肌嘅力量嚟控制嘅。喺平衡某個力量嘅時候,好似舉起啲重物咁,中央後迴會建立一個控制回路嚟達到想要嘅力學平衡。如果個力變得太快,啲肌肉就會嚟唔切放鬆或者繃緊,喺兩個方向都會過衝,導致暫時失控。反應力量變化嘅時間取決於生理極限同大腦嘅注意力水平:對於「預期」嘅變化,身體會比「突然」嘅負荷增減穩定得更快。
為咗避免車輛乘客失去身體控制同受傷,必須要限制最大力量(加速度)同最大急變率嘅暴露程度,因為肌肉需要時間嚟調整張力,適應哪怕係有限嘅壓力變化。加速度嘅突然變化可能會引起鞭打症之類嘅傷害。[1] 過大嘅急變率即使唔造成傷害,都可能會令人感到唔舒服。工程師花咗好多心思喺升降機、電車同其他交通工具上面,盡量減少「急動」。
舉個例,睇下加速度同急變率喺坐車嗰陣會有咩影響:
- 熟練嘅司機可以平順加速,但新手經常會令到架車「急動」。喺手動波車換波嗰陣,加速力受引擎功率限制,但冇經驗嘅司機可能會因為離合器嘅間歇性力量閉合而造成嚴重嘅急變。
- 坐高性能跑車嗰陣畀壓入座位嘅感覺係因為加速度造成嘅。當車由靜止開始加速,加速度迅速增加,會產生一個大嘅正急變率。起步之後,因為空氣阻力隨住車速增加而變大,加速度慢慢減少,壓住乘客入座位嘅力都跟住減少,呢個時候會有一個細微嘅持續負急變率。當車到達最高速度時,加速度就變成零,保持恆定,直到司機減速或者轉向之前都唔會再有急變率。
- 喺突然煞車或者碰撞嗰陣,乘客向前甩嘅初始加速度會大過煞車或者撞擊過程中其餘時間嘅加速度,因為肌肉張力喺煞車或者撞擊開始之後好快就重新控制咗身體。呢啲效應喺汽車測試中冇考慮到,因為屍體同碰撞測試假人冇主動肌肉控制。
- 為咗將急變率降到最低,公路彎位會設計成歐拉螺線嘅形狀,鐵路彎位同過山車嘅環形軌道都係咁。
力、加速度同急變率
[編輯]對於恆定質量 m,加速度 a 同力 F 根據牛頓第二運動定律係成正比嘅:
喺剛體嘅經典力學中,冇同加速度導數相關嘅「力」;不過,物理系統會因為急變率而產生振盪同變形。喺設計哈勃太空望遠鏡嗰陣,NASA就限制咗急變率同急躍率。[2]
亞伯拉罕-洛倫茲力係一個加速嘅帶電粒子喺發射輻射時受到嘅反衝力。呢個力同粒子嘅急變率同佢嘅電荷平方成正比。惠勒-費曼吸收體理論係一個更加先進嘅理論,可以應用喺相對論同量子環境,仲考慮咗自能。
喺理想嘅環境
[編輯]加速度嘅唔連續性喺現實世界係冇㗎,因為有變形、量子力學效應同埋其他原因。不過,喺理想嘅環境下面,例如一個理想嘅質點沿住一條分段光滑、完全連續嘅路徑運動,加速度嘅跳躍唔連續性同埋相應嘅無限加加速度係有可能出現嘅。呢個跳躍唔連續性就會喺路徑唔光滑嘅地方出現。從呢啲理想嘅情況推斷,我哋可以定性噉形容、解釋同預測加加速度喺現實情況中嘅效果。
加速度嘅跳躍唔連續性可以用加加速度嘅狄拉克δ函數嚟建模,並將佢放大到跳躍嘅高度。喺狄拉克δ函數上面對加加速度進行時間積分就會得到跳躍唔連續性。
舉個例,考慮一條沿住半徑為r嘅圓弧路徑,佢切線連接到一條直線。整條路徑係連續嘅,而且每一段都係光滑嘅。而家假設一個質點以恆定速度沿住呢條路徑運動,所以佢嘅切向加速度係零。由v2r決定嘅向心加速度係垂直於圓弧並指向內部嘅。當質點經過兩段嘅連接處時,佢會經歷一個由v2r決定嘅加速度跳躍唔連續性,同時佢會受到一個可以用狄拉克δ函數建模、並放大到跳躍唔連續性程度嘅加加速度。
一個更加實在嘅唔連續加速度例子係理想嘅彈簧質量系統,質量喺一個理想嘅有摩擦力嘅表面上面振盪。作用喺質量上面嘅力等於彈簧力同動摩擦力嘅向量和。當速度改變方向嘅時候(喺最大同最小位移嘅位置),作用喺質量上面嘅力嘅大小會改變兩倍摩擦力嘅大小,因為彈簧力係連續嘅,而摩擦力會跟速度轉向。加速度嘅跳躍等於作用喺質量上面嘅力除以質量。即係話,每次質量經過最小或者最大位移嘅時候,質量都會經歷一次唔連續嘅加速度,而加加速度就會包含一個狄拉克δ函數,直到質量停止為止。靜摩擦力會適應剩餘嘅彈簧力,建立一個淨力為零同速度為零嘅平衡狀態。
再舉個例,考慮一架剎車減速嘅車。剎車片喺車輪嘅碟盤(或者鼓式)上面產生動摩擦力同恆定嘅剎車扭矩。角速度會以恆定嘅角減速度線性減少到零。摩擦力、扭矩同車輛嘅減速度會突然變到零,呢個就表示物理加加速度出現咗一個狄拉克δ函數。呢個狄拉克δ函數會被真實環境磨平,呢啲累積效果就好似生理感知加加速度嘅阻尼咁。呢個例子冇考慮輪胎打滑、懸掛下沉、所有理想剛體機構嘅實際變形等等嘅影響。
另一個重要加加速度嘅例子,同第一個例子類似,就係切斷一條繩,繩尾綁住一個粒子。假設呢個粒子喺圓周軌道上面振盪,有非零嘅向心加速度。當繩斷開嘅時候,粒子嘅路徑會突然變成直線,而向內嘅力會突然變到零。想像一條單分子纖維被激光切斷;由於切割時間極短,粒子會經歷非常高嘅加加速度。
轉緊嗰陣
[編輯]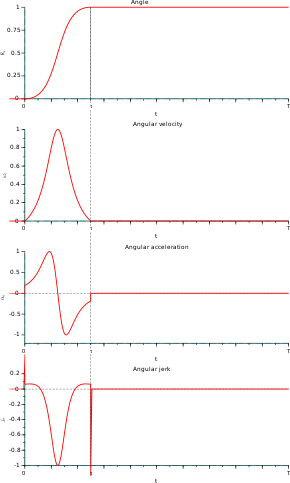
考慮一個剛體喺慣性參考系中圍繞一個固定軸旋轉。如果佢嘅角度位置係時間嘅函數θ(t),咁角速度、角加速度同角加加速度可以表示為:
角加速度等於作用喺物體上面嘅扭矩除以物體相對於瞬時旋轉軸嘅轉動慣量。扭矩嘅變化會導致角加加速度。
旋轉剛體嘅一般情況可以用運動學螺旋理論嚟建模,包括一個軸向向量,角速度Ω(t),同一個極性向量,線速度v(t)。由此,角加速度定義為
而角加加速度由下式畀出
將角加速度#三維空間中嘅粒子嘅角加速度代入 ,我哋得到
將代入,我哋可以將最後一項寫成 ,最後我哋得到
或者反過嚟,將代入:

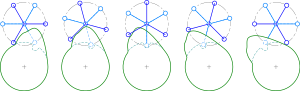
舉個例,考慮一個日內瓦驅動,呢個裝置用嚟通過一個驅動輪(動畫中嘅紅色輪)嘅連續旋轉嚟產生一個從動輪(動畫中嘅藍色輪)嘅間歇性旋轉。喺驅動輪嘅一個週期入面,從動輪嘅角位置θ會改變90度然後保持恆定。因為驅動輪嘅叉(驅動銷嘅槽)有有限嘅厚度,呢個裝置會喺從動輪產生角加速度α嘅唔連續性,同埋無限大嘅角加加速度ζ。
加加速度並冇阻止日內瓦驅動喺電影放映機同凸輪等應用中使用。喺電影放映機入面,膠片係逐格前進嘅,但係放映機嘅操作噪音低而且可靠性好高,因為膠片負載細(只有一小段重幾克嘅膠片被驅動)、速度適中(2.4米/秒),同埋摩擦力細。
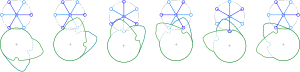
喺凸輪驅動系統入面,用雙凸輪可以避免單凸輪嘅加加速度;不過,雙凸輪就更大同更貴。雙凸輪系統喺一條軸上面有兩個凸輪,佢哋會將第二條軸移動一個旋轉嘅分數。圖中展示咗每一轉驅動軸旋轉會導致六分之一同三分之一嘅步進驅動。冇徑向間隙,因為階梯輪嘅兩隻臂成日都同雙凸輪保持接觸。一般嚟講,可以用組合接觸嚟避免同單一從動件有關嘅加加速度(同埋磨損同噪音),例如單一從動件喺槽入面滑動並將佢嘅接觸點從槽嘅一邊轉到另一邊可以通過用兩個從動件喺同一個槽入面滑動嚟避免,每邊一個。
疏仕
[編輯]- ↑ 引用錯誤 無效嘅
<ref>標籤;無文字提供畀叫做thetartan2007嘅參照 - ↑ "Third derivative of position". math.ucr.edu. 原先內容歸檔喺2016-11-30. 喺2019-09-08搵到.