古典力學
古典力學(粵拼:gu2 din2 lik6 hok6)[e 1],又叫牛頓力學[e 2],喺物理學上係指力學嘅兩大分枝之一。古典力學呢套理論框架,係由英國科學家牛頓同德國哲學家萊布尼茲搞起嘅,主要研究宇宙入面嘅物體點樣喺力嘅影響下郁動。
古典力學研究嘅題目好古老,但要到咗 17 世紀有牛頓等嘅思想家研究,先至有飛躍嘅發展。古典力學用咗幾條相對簡單嘅物理定律,嘗試解釋嗮宇宙入邊一切物體嘅郁動——即係話佢解釋現象嘅能力勁得嚟又好簡潔[3][4],所以牛頓等人提出呢套理論後嗰幾個世紀,呢套理論框架一路都好有影響力,要等到成廿世紀初現代物理學成形之後,古典力學先至開始喺理論性質嘅研究當中喪失影響力[5][6]。
一般嚟講,古典力學喺符合咗兩個條件嘅環境下會俾到極之準嘅預測:
當呢兩個條件當中是但一個達唔到嗰時,用古典力學計出嚟嘅結果會冇晒準確度-研究得原子咁細(或者更細)嘅嘢嗰陣要用量子力學先得,而研究一啲速度接近光速嘅嘢嗰陣就要用相對論至得。所以一去到進階嘅物理學研究(呢啲研究成日都會分析細粒過原子或者以接近光速飛嘅嘢),物理學家實係會用後者等嘅高階理論,而唔會用古典力學。不過喺一般地球環境下,呢兩個條件幾乎實會成立,所以古典力學就算到咗廿一世紀都仲係喺好多工程領域上有用[3][7]。
假設同三大參數
[編輯]
古典力學係一個有相當高簡潔度嘅科學理論,噉講意思即係話,呢個理論框架淨係用咗少數幾個假設同埋概念就解釋得到好多現象。古典力學假設咗空間係跟歐幾里得幾何[e 3]嘅[8],並且會將分析緊嘅物體抽象化噉諗做點質量[e 4]-即係容量係 嘅細點,而一個點質量有三個基本參數[9]:
淨係靠呢幾個參數,古典力學就能夠完整噉分析件物體嘅郁動(睇埋奧坎剃刀)。
要留意嘅係,古典力學只係現實嘅大致近似[e 8]:例如古典力學分析得到嘅有質量物體實係有非零容量嘅,所以點質量嘅假設查實就唔符合現實;之但係力學研究說明咗,「當啲嘢係點質量」呢個做法計到出嚟嘅結果大致正確-誤差極之細,即係就算一嚿物體係有非零容量嘅,佢喺古典力學入面嘅行為同「一柞點質量」冇明顯分別,而一嚿噉嘅物體嘅重心[e 9]行為同一粒點質量冇分別,所以就算假設咗嚿物體係點質量,計算得出嘅結果都同現實冇明顯差異。因為噉,呢種抽象化嘅做法一般都俾科學界認為係可以接受嘅[3][9]。
位置同郁動
[編輯]
古典力學嘅基礎係「位置」嘅概念,而其餘嘅重要概念大部份都可以由位置嗰度推導出嚟:
位置
[編輯]位置[e 10]係古典力學嘅一個基本概念,可以用坐標系統[e 11]表達。要用一個坐標系統表達物體嘅位置,就要
一件物體嘅位置就係由呢啲坐標值嚟表達。例如如果分析緊嘅空間得一條直線,可以揀佢上面是但一點做原點整返個一維(1D)嘅坐標系統,當原點嘅左手邊做正值,噉喺原點左手邊一米嘅嘢嘅位置就係 米,而喺原點右手邊兩米嘅嘢嘅位置就係 米;如果分析緊嘅空間係個正方形,就可以揀佢左下角做原點整返個二維(2D)嘅坐標系統,呢個系統會有 X 同 Y 兩條軸,分別以向右同向上做正值,噉喺呢個空間入面,嗰個正方形嘅右上角嘅位置就會係 米- 係個正方形嘅長度,而 係個正方形嘅闊度;最後,一般現實世界會攞古典力學嚟分析嘅空間都係三維(3D)嘅-會有長度、闊度、同埋高度三個坐標值。而且喺二維或者以上嘅空間入面,唔同嘅線之間仲有角度呢個變數要考慮,角度都有得攞嚟表達物體嘅位置(睇附圖)[10]。
一件物體嘅郁動[e 14]可以理解成佢位置隨住時間嘅改變。順帶一提,喺包括古典力學嘅古典物理學入面,時間一般俾人當係絕對[e 15]嘅-即係話古典物理學家覺得時間流動呢家嘢無論由邊個觀察者嘅角度睇都係一樣嘅,如果有兩件事件之間隔咗一秒發生,噉任何一個觀察者所睇到嘅「呢兩件事件之間嘅時間距離」都會係一秒。事實上,廿世紀狹義相對論嘅研究說明咗呢個諗法係啱唔嗮嘅,但喺一般地球環境之下,呢個「絕對時間」嘅假設都仲係啱用嘅[11][12]。
位移
[編輯]位移[e 16]係指一件物體喺位置上嘅改變,喺古典力學計數嗰陣成日會用。假設有件物體由 呢個位置郁去新位置 嗰度,佢嘅位移-寫做「」或者「」-就係 ,例如有件物體喺一個三維空間入面由 呢點郁去 嗰點度,佢嘅位移就係 -等如 。位移係有方向嘅物理量-即係一個向量[e 17],所以除非係喺一維空間,一個位移冇得淨係用一個數值表達得嗮,而係要用好幾個數值嚟表達[13]。
位移同距離[e 18]係兩個唔同嘅概念:假如一件物體用一條非直線嘅路線移動,噉佢行過嘅路線反映佢行咗嘅距離,而位移會係佢起點同終點之間嘅直線距離[13]。以下圖想像:彎彎曲曲嗰條線表示嘅係距離,而直嗰條線表示嘅係位移。

速度同速率
[編輯]
喺古典力學當中,速度[e 19]嘅正式定義係「位移對時間嘅導數」(詳情可以睇微積分[14])-呢個詞用日常語言講嘅話,就係「位移隨住時間改變嘅率」,用方程式表達係[15]:
- ;當中, 係速度,而 就係成個過程用咗嘅時間。
例如有件三維嘅物體喺 10 秒之間由原點郁去 嗰點,佢嘅速度就係[15]
- ;
因為位移係個向量,所以速度都係一個向量。如果上述嘅距離係以米做長度嘅單位,呢個向量表示「件物體嘅速度沿 X 軸係 0.4 米每秒,沿 Y 軸係 0.3 米每秒,沿 Z 軸係 0 米每秒」。呢件物件行咗嘅距離(用畢氏定理計到)係 5 米,所以佢嘅速率([e 20]指唔考慮方向,淨係諗個速度嘅值,即係「行咗嘅距離除時間」)就等如[15]
- - 米每秒。
要留意嘅係,喺嚴格嘅物理學用詞嗰度,「速度」同「速率」係兩個唔同嘅概念:前者係一個向量-一個有方向嘅物理量-所以要用好幾個數字先表達得嗮佢包含嘅所有內容(即係件物體由三條軸睇分別郁咗幾多);而後者係一個唔考慮方向嘅標量[e 21],淨係包含咗「件物體郁得幾快」,所以用一個數字已經能夠表達到嗮佢包含嘅內容。雖然係噉,喺日常用語入面,啲人用起「速度」同「速率」呢兩個詞上嚟都好求其,一般都當正佢哋係同義詞噉[15]。
相對速度
[編輯]因為速度係一個向量,所以佢有得就住方向嚟做加減,計出相對速度[e 22]:兩件物體之間嘅相對速度定義上係指「如果將其中一件物體當成靜止做對照點,另外嗰件物體嘅速度望落會係幾多」;舉個例說明,有一個人喺一個火車嘅車頂向車頭行(為咗簡單起見,淨係考慮佢哋沿「東同西」呢條軸嘅郁動),架火車相對地面係向東以時速 公里行[註 1],而個人喺車頂以相對架火車係向東以時速 公里行-如果將架火車想像成係靜止嘅,個人嘅速度係「向東時速 公里」,不過由一個喺地面嘅靜止觀察者嚟講,嗰個人就係以向東時速 公里()行緊。即係將唔同嘅物體嘅速度相加可以知道佢哋嘅相對速度[註 2]-呢樣嘢速率做唔到,因為速率唔包含方向,將兩架車嘅速率就噉相加減唔會俾分析嗰個人知道兩架車嘅相對速度[16]。

再抽象些少講嘅話就係:設第一架車嘅速度做 ,第二架車嘅速度做 ;其中兩架車嘅速率就分別係 同 ,而 同 分別係兩架車向住佢哋個方向嘅單位向量[e 23]。噉由第二架車嗰度望,第一架車嘅速度 係[16]
同一道理,由第一架車嗰度望,第二架車嘅速度 係
如果呢兩架車嘅郁嗰條軸一樣,,噉呢條公式簡化咗就係
加速度
[編輯]
加速度[e 24]喺定義上係「速度對時間嘅導數」-同一道理,用日常語言講出嚟嘅話就係「速度隨住時間改變嘅率」,用方程式表達嘅話係[17]:
- ; 就係加速度。
例如係附圖噉。附圖顯示一件物體由靜止(),去到有一個非零嘅速度(),再撞到地下停低(),期間 不斷有變,即係話 。
加速度都係一個向量,反映咗「速度改變得有幾快」。要留意嘅係,因為加速度係向量,所以就算佢係負數,都唔一定代表件物體係減緊速。例如有件物體,佢個加速度係 米每二次方秒。呢個數字表示佢個速度以每秒「 米每秒」嘅率噉改變緊,噉樣可以表示兩樣嘢[17][18]:
- 可能件物體嘅速度喺一秒之間由「 米每秒」變做「 米每秒」-即係一個減速,但佢個速度由頭到尾都仲係向住正方向嘅;又或者係
- 佢個速度喺一秒之間由「 米每秒」變做「 米每秒」-呢個反而係一個向住負方向嘅加速。
參考系
[編輯]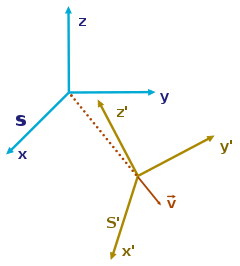
參考系[e 25]喺物理學入面係指「用嚟測量同埋紀錄其他物體嘅屬性嘅坐標系統」。喺做古典力學分析嗰陣,首先要做嘅嘢係搵返個點做原點,呢樣嘢係夾硬嚟[e 26]嘅-現實世界嘅空間入面冇啲乜嘢原點(雖然古典力學假定咗有),如果有兩件物體喺同一條打橫嘅直線上相距 1 米:噉有得揀左邊嗰件做原點,當右手邊做正,而喺呢個情況下右邊嗰件物體嘅位置會係( 米);又可以揀左邊嗰件做原點,左手邊做正,而喺呢個情況下右邊嗰件物體嘅位置會係( 米)。即係話揀參考系-揀邊點做原點同埋邊個方向做正負-係隨意嘅,只要揀好咗之後喺接住落嚟嘅分析嗰度一致噉使用,計出嚟嘅結果就唔會有問題[19][20]。
假想而家有一粒以若干非零速度郁緊嘅粒子,由兩個唔同嘅參考系 同埋 嗰度量度佢。又假想相對於 呢個參考系, 呢個參考系以 嘅速度郁緊(為咗簡單起見,呢個例子淨係考慮佢哋沿一個軸嘅郁動)。噉企喺呢兩個參考系嗰度嘅觀察者會分別噉量度到以下嘅結果[20]:
一個可能要計呢啲數嘅情況係一個天文學研究:有兩個觀察者,一個企喺地球,另一個企喺月球,兩個都當自己係原點喺度嘗試測量火星嘅郁動(三樣嘢都郁緊)-雖然喺呢個情況,條數要計 3 次,因為呢柞天體各自喺空間嘅三條軸嗰度都有位移,喺三條軸嗰度都有速度值[21]。
力以及能量
[編輯]動量
[編輯]喺古典力學入面,線性動量[e 27],簡稱動量,數學符號係 ,指係一件物體嘅質量同佢速度乘埋得出嘅數[22][23]:
- ,當中 係件物體嘅質量。
動量有以下嘅特性:動量同速度一樣係向量,有方向同數值,喺國際單位制[e 28]嗰度嘅單位係公斤米每秒-公斤(質量嘅單位)同米每秒(速度嘅單位)乘埋;用日常用語講嘅話,動量表達咗一件物體撞落去第啲嘢嗰陣,會有幾能夠引致後者嘅郁動有所改變-假設有一個檯波,佢以一定嘅速度撞落去第個檯波嗰度,假設第啲因素不變,如果前者嘅速度愈快或者質量愈大(兩者都可以引致動量上升),噉後者俾佢撞完之後嘅郁動嘅改變幅度會愈大[24]。
根據動量守恆定律[e 29],喺一個封閉系統(唔能夠由外界攞動量)入面,所有物體嘅動量嘅總和永遠都唔會變-如果有嚿物體撞落去一嚿本嚟唔郁嘅嘢嗰度嘅話,後者會吸收動量並且加速,而前者實會少噉咗啲動量而減速-碰撞呢家嘢本質上可以想像成「動量嘅轉移」[25]。
|
力
[編輯]
力(單位係牛頓)呢個概念同動量息息相關。牛頓係人類史上第一個用數學方程式嚟表達「力」呢個概念嘅人,而根據牛頓第二定律[e 30],力係靠動量嚟定義嘅[26]:
呢條式講嘅係「作用喺一件物體上面嘅力」()等如「佢前前後後嘅動量改變」()除以「呢個作用所維持嘅時間」()。即係話假設所有因素唔變,作用喺嗰件物體上面嘅力愈大(簡單啲講就係愈大力推或者拉佢),件物體嘅動量改變會愈大;而如果個力保持唔變,作用持續嘅時間愈短,件物體嘅動量改變都會愈大。假定件物體喺成個作用嘅過程入面質量唔變,因為「速度隨時間嘅變率」等如加速度(),第二定律條式仲有得簡化做[26]:
自由體圖
[編輯]自由體圖[e 31]係古典力學分析上嘅一種做法,喺物理學同工程學上都好常用:一幅自由體圖會畫出分析緊嗰一件物體、件物體嘅各部份、以及向件物體施力嘅物體,然後用箭咀表示出個系統當中存在嘅力,每個箭咀會有個方向代表嗰股力嘅方向,仲會附帶一個數值表示嗰股力嘅大細;例如想像一嚿物體(用一個藍色嘅四方形代表),擺咗喺一個斜面(紅色三角形)上面,個斜面同地面之間嘅角度係 咁多度,件物體會受到至少三股力-
如果 [註 3],就會令嚿物體沿 嘅向左下方向有個加速度,而佢向嗰個方向嘅速度就會上升。畫做自由體圖嘅話[27][28]:

好似上述噉嘅圖喺(例如)建築設計上可以用嚟分析喺一間建築物嘅入口隔離、用嚟俾輪椅行嘅斜路嘅力學設計(將藍色四方形想像成一架輪椅)[29]。
能量概念
[編輯]作功
[編輯]如果喺一個特定嘅參考系入面,有一股力 持續噉施落一件有質量嘅物體嗰度,而且喺成個過程期間,件物體行咗 [註 4] 咁遠嘅位移,用 C 代表佢行嗰條軌跡。因為成個過程入面有股力作用喺佢身上,件物體會有個非零嘅加速度,而有個非零嘅加速度代表佢個速度同動量會係噉變。成個過程入面,「嗰股力嘅作功[e 34]」係一個冇方向嘅標量,定義上係[30]:
- ,或者寫做
- 。
如果喺成個過程入面股力個數值唔一致,噉個功嘅值可以用積分(詳情睇微積分相關)嘅方法計:
|
例如想像一個棒球投手投球,啱啱開始嗰陣,個波喺佢手中唔郁(),而由「開始投」到「放手」期間,佢一路用佢隻手向個波施力,而喺呢段期間個波移動咗若干嘅距離(),令個波最後以若干非零速度()飛出去[31]。
順帶一提,如果有一股力,佢喺件物體身上作嘅功嘅數值總量係(只要移動嘅起點同終點不變)無論件物體嘅移動軌跡係點都一樣嘅話,呢股力就係一股保守力[e 35],例如重力就係一股保守力,而摩擦力唔係[32]。
動能
[編輯]
有咗功呢個概念,就有得去諗力學入面有關能量[e 36]嘅問題[33]。首先,根據運動方程[e 37][34],
- ,
呢條式描述一件加速緊嘅物體嘅速度變化,當中 係件物體嘅最後速度, 係佢初頭個速度。跟手執吓呢條式就會變成
- ,即係
- ,跟住代呢條式落去功嗰條式()嗰度嘅話就會出到
- ,跟住一路執:
- ,
- 。
最尾呢條式表示,當有股力喺一件物體上作功,令後者速度改變嗰陣,屬於件物體嘅某個物理量會有所改變,而呢個物理量同件物體嘅「質量」以及「速度嘅次方」成正比。呢個物理量係物理學上面所講嘅動能[e 38]-物體因為佢哋嘅郁動而帶嘅能量。由呢條式嗰度,仲有得推導埋白努利定律[e 39]出嚟[35]。
位能
[編輯]
除咗動能之外,力學能量仲有所謂嘅位能[e 40]-物體因為喺某啲力場入面嘅位置而有嘅能量。喺一個引力場[e 41]入面,要將一件物體移離個引力場嘅中心就要抵抗引力場持續施喺件物體上嘅引力:如果除咗引力之外冇任何嘅力施件物體,俾佢自由下墜[e 42]嘅話,佢會因為受引力場嘅力吸引而傾向向住個引力場嘅中心加速(牛頓第二定律)。假想有件物體喺一粒行星嘅引力場入面,唔受干擾噉樣受到股引力 向住粒星嘅中心跌落嘅話,佢跌咗某段距離 之後,股引力喺佢身上作咗嘅功 就會等如[36]:
而如果要施股力 ,將一件物體喺個引力場當中移離引力場中心 嘅距離,期間速度恆定不變-,,,就總共要施以 咁多嘅作功。順帶一提,呢條式假設咗 同粒行星嘅直徑比起上嚟好細,所以喺成個過程入面 嘅數值可以當冇變(詳情睇牛頓萬有引力定律)[9]。
如果件物體係自由下墜,件物體因為受咗引力,所以會加速,而佢嘅速度升表示佢帶嘅動能會跟住升。如果件嘢冇因為受空氣阻力而減速嘅話,根據能量守恆定律,佢失去嘅位能會等如佢得到嘅動能,即係話:
由呢條式嗰度可以睇得到「一件物體受嘅引力」、「佢自由下墜咗嘅距離」同埋「佢嘅動能改變」之間成嘅數學關係。用呢柞式計到出嚟嗰啲結果(考慮埋空氣阻力呢啲拉雜嘢嘅話)同實驗得出嘅結果吻合,所以呢柞式廣受物理學界採用[9]。
動能同位能喺物理學同埋好多工程學領域上都係不可或缺嘅概念。例如想像家陣有架過山車由路軌頂點向下衝,期間架車會加速得到動能,架車所得嘅動能嘅量局部取決於架車喺頂點嗰陣嘅位能嘅量。頂點位能嘅量可以用相對簡單嘅數(頂點嘅高度等)估計,所以動能同位能嘅概念可以攞嚟幫手估計架過山車向下衝嗰陣嘅最高速度會係幾多,而知道過山車嘅最高速度對於評估過山車嘅安全嚟講有用[37]。詳情可以睇埋過山車物理嘅嘢[38]。
|
物理定律
[編輯]古典力學理論框架當中有多條定律。呢啲定律做嘅嘢係用方程式描述質量、位置以及力彼此之間或者同第啲物理量成乜關係。
牛頓運動定律
[編輯]
牛頓運動定律[e 43]係由牛頓提出,描述物體嘅郁動同力之間嘅關係嘅三條物理定律,係古典力學理論框架嘅基礎。靠住呢三條定律,物理學家有得推理出各種各樣嘅力學定律出嚟,例如係描述行星點圍住恆星轉嘅開普勒定律[e 44]噉[26][39]。
第一定律
[編輯]牛頓第一定律[e 45]講,唔受外力影響(施加喺嚿物體上嘅淨力等如 )嘅物體會持續佢本身嘅運動()-本嚟唔郁嘅會保持唔郁,郁緊嘅會繼續以佢本身嘅速度郁。用方程式表達嘅話就係[40]:
- ;或者
- [註 5]。
呢條定律亦都暗示咗:
呢條定律引申咗慣性[e 47]嘅概念-慣性嘅定義係指喺第一定律入面,物體有一種保持本嚟運動狀態嘅傾向[39]。
第二定律
[編輯]
牛頓第二定律[e 48]講,物體嘅加速度同施喺佢上面嘅淨力成正比,同嚿物體嘅質量成反比,方向同淨力嘅方向一樣。用方程式表達嘅話[41]:
而喺數學上,牛頓第二定律通常寫做:
呢度定義咗「質量」就係淨力同加速度之間嘅比率。呢個意義下嘅質量就係所謂嘅慣性質量[e 49]-即係當咗質量只不過係加喺嚿物體上嘅淨力同加速度相除得出嘅數值。喺國際單位制入面,力、加速度同埋質量嘅單位分別俾人規定做牛頓(Newton,)、公尺每二次方秒(m/s2)同埋公斤(kg)。施加 1 牛頓嘅力落質量係 1 公斤嘅物體度可以令到嚿物體嘅加速度變做 1 m/s2。亦即係話[39]:
第三定律
[編輯]牛頓第三定律[e 50]講,作用力[e 51]同反作用力[e 52]嘅數值大細一樣,但方向就啱啱相反。當有一股力被施加喺一嚿物體上嗰陣(作用力),嗰嚿物體實會產生出另外一股大細相等得嚟方向又相反方向嘅力(反作用力)。呢條定律用方程式表達嘅話係噉嘅[42]:
當中 係物體 B 施喺物體 A 上面嘅力, 係物體 A 施喺物體 B 上面嘅力。由呢條式入面睇得出,兩股力嘅數值係相等嘅,而個負號就表示咗兩股力方向相反-擺喺一個一維座標系統入面嘅話,佢哋一定會係一個向正方向一個向負方向,而且反作用力同作用力嘅物理本質應該係完全一樣嘅-如果作用力係一股萬有引力嘅話,噉反作用力都係一股萬有引力[42]。
萬有引力定律
[編輯]萬有引力定律[e 53]呢條定律話:宇宙入面嘅粒子(當佢哋係點質量)冚唪唥都會向第啲粒子施加一股穿過佢哋之間嘅連心線嘅吸引力;另外,一粒粒子施加落另一粒粒子嘅引力同另外嗰粒粒子施落自己嘅力數值一樣,而呢個數值係同呢兩粒粒子嘅質量成正比,但同佢哋之間嘅距離嘅平方成反比(「A 施喺 B 身上嘅萬有引力」同「B 施喺 A 身上嘅萬有引力」彼此係作用力同反作用力),同佢哋嘅化學性質或者其他物理性質無關,即係話[43][44]:
- 係兩件嘢之間嘅引力嘅數值;
- 係萬有引力常數;數值係 6.674×10−11 N • (m/kg)2 [45]。
- 係第一件嘢嘅質量;單位係公斤(kg)。
- 係第二件嘢嘅質量;單位係公斤(kg)。
- 係兩件嘢之間嘅距離;單位係米(m)。

第啲定律
[編輯]
... 等等。
適用範圍
[編輯]古典力學喺研究一般地球環境下嘅物體嗰陣,都係適用嘅:喺呢種環境之下啲物體嘅尺寸大過原子好多,而且速度又低過光速一截,所以喺廿世紀打前,古典力學一路都好好用;但喺廿世紀初,人開始研究得原子咁大粒嘅物體同埋一啲以接近光速郁動嘅物體,於是發覺用古典力學嚟分析呢啲嘢嗰時計到嘅結果錯嗮,同實驗觀察到嘅結果完全唔同。喺呢個時代,好似愛因斯坦等嘅物理學家就提出咗相對論同量子力學等嘅學說,先至令科學界更加深入噉了解到呢啲嘢嘅本質。一般嚟講,古典力學可以話只不過係相對論同埋量子力學嘅一個特殊情況[9][47]。
古典力學喺兩個條件成立之下,先會適用:
條件 1:速度
[編輯]首先,啲嘢要速度明顯低過光速。喺古典力學當中,一粒粒子嘅動量 係
其中 係粒粒子嘅質量,而 係佢嘅速度。
而喺狹義相對論[e 58]入面,一粒粒子嘅動量係[48][49]
其中 係粒粒子嘅靜止質量[e 59],而 係光速。由呢條式入面睇得到,當粒粒子嘅速度低過光速好多()嗰陣, ≈ ,所以 嘅開方 ≈ , ≈ -用文字講嘅話,當一粒粒子嘅速度低過光速好多嘅時候,用古典力學計到嘅結果會同用狹義相對論計到嘅近乎一樣,但當粒粒子嘅速度愈嚟愈接近光速,用古典力學計到嘅結果同用狹義相對論計到嘅之間嘅差異會愈嚟愈大(而實驗結果都係撐狹義相對論),直至去到某一個點,古典力學計到嘅結果會同實驗數據得出嘅差異大到冇可能再靠古典力學-物理學界就係喺廿世紀初撞到呢一點。因為噉,廿一世紀嘅物理學研究唔會再用古典力學,而係會用相對論,不過因為古典力學喺一般地球環境之下都仲係啱用,而且佢啲方程式比較簡單,所以工程學好多時都仲係會用古典力學嚟計數[48]。
條件 2:尺度
[編輯]除此之外,啲嘢要尺度明顯大過原子。
量子力學[e 60]係廿世紀崛起嘅一個物理學理論,講到物質波[e 61]嘅概念,指出物質全部都會波動噉嘅特性,會有繞射(波動通過物件嘅邊緣嗰陣會轉彎嘅現象)等嘅行為[50][51]。根據德布羅意假說[e 62],一粒非相對論型粒子(指速度明顯低過光速嘅粒子,分析呢啲粒子嘅郁動唔使用到相對論)嘅波長-即係所謂嘅德布羅意波長[e 63]可以用以下嘅式計:
- ,
其中 係普朗克常數[e 64],而 就係粒粒子嘅動量。一般嚟講,當研究緊嘅系統尺度接近德布羅意波長嗰陣,個系統會顯現出明顯嘅波動特性,而因為喺一般環境下物質嘅波動特性唔明顯,古典力學並冇考慮呢啲效應,所以古典力學喺研究緊嘅系統尺度接近德布羅意波長嗰時會做唔到準確嘅預測[50]。
|
子領域
[編輯]
古典力學可以分做多個子領域:
- 靜力學,專門分析唔加速嘅物理系統之下嘅力結構,例如研究靜止嘅建築物點樣因為受嘅淨力係 0 而企到喺度唔郁[52]。
- 動力學,專門分析力點樣影響物體嘅郁動,例如用牛頓運動定律研究球類運動當中嘅波點樣受各種力嘅影響而郁動[53]。
- 運動學,專門用唔用到「力」呢個概念嘅數學模型嚟模擬點、物體或者多件物體組成嘅系統嘅郁動,例如用一個冇力喺入面嘅函數描述機械組成部份嘅週期郁動[54]。
- 連續介質力學將物體想像成連續嘅一大嚿物料(而唔係離散嘅粒子)嚟分析物體嘅力學行為[55]。
- 統計力學建基於概率論,嘗試思考物體嘅整體特性(例如係溫度)點樣源自組成嚿物體嘅粒子嘅微觀力學行為[56]。
... 等等。
相關領域
[編輯]相關應用
[編輯]古典力學喺以下呢啲領域當中都會廣泛噉俾人採用嚟模擬物體喺力之下嘅行為:
... 等等。
睇埋
[編輯]註釋
[編輯]參考
[編輯]- ↑ classical mechanics
- ↑ Newtonian mechanics
- ↑ Euclidean geometry
- ↑ point mass
- ↑ mass
- ↑ position
- ↑ force
- ↑ approximation
- ↑ center of mass
- ↑ position
- ↑ coordinate system
- ↑ origin
- ↑ dimension
- ↑ motion
- ↑ absolute
- ↑ displacement
- ↑ vector
- ↑ distance
- ↑ velocity
- ↑ speed
- ↑ scalar
- ↑ relative velocity
- ↑ unit vector
- ↑ acceleration
- ↑ frame of reference
- ↑ arbitrary
- ↑ linear momentum
- ↑ SI Units
- ↑ law of conservation of momentum
- ↑ Newton's second law
- ↑ free body diagram
- ↑ friction
- ↑ reaction
- ↑ work done
- ↑ conservative force
- ↑ energy
- ↑ equations of motions
- ↑ kinetic energy
- ↑ Bernoulli's principle
- ↑ potential energy
- ↑ gravitational field
- ↑ free fall
- ↑ Newton's laws of motion
- ↑ Kepler's laws of planetary motion
- ↑ Newton's first law
- ↑ net force
- ↑ inertia
- ↑ Newton's second law
- ↑ inertial mass
- ↑ Newton's third law
- ↑ action
- ↑ reaction
- ↑ Newton's law of universal gravitation
- ↑ Hooke's law
- ↑ d'Alembert principle
- ↑ Euler's equations
- ↑ Hamilton's principle
- ↑ special theory of relativity
- ↑ rest mass
- ↑ quantum mechanics
- ↑ matter wave
- ↑ De Broglie hypothesis
- ↑ De Broglie wavelength
- ↑ Planck constant
- ↑ double-slit experiment
- ↑ Ceanga, V., & Hurmuzlu, Y. (2001). A new look at an old problem: Newton's cradle. J. appl. mech., 68(4), 575-583.
- ↑ Barfield, W. R. (1998). The biomechanics of kicking in soccer. Clinics in sports medicine, 17(4), 711-728.
- ↑ 3.0 3.1 3.2 3.3 3.4 French, A.P. (1971). Newtonian Mechanics. New York: W. W. Norton & Company.
- ↑ Bettini, Alessandro (2016). A Course in Classical Physics 1-Mechanics. Springer. p. vii.
- ↑ Kleppner, Daniel; Kolenkow, Robert (2014). An Introduction to Mechanics (2nd ed.). Cambridge: Cambridge University Press. p. 49.
- ↑ Thornton, Stephen T.; Marion, Jerry B. (2004). Classical dynamics of particles and systems (5. ed.). Belmont, Calif. [u.a.]: Brooks/Cole. p. 50
- ↑ Feynman, Richard (1999). The Feynman Lectures on Physics. Perseus Publishing.
- ↑ "MIT physics 8.01 lecture notes (page 12)" (PDF). 原著 (PDF)喺2013年7月9號歸檔. 喺2018年1月28號搵到.
- ↑ 9.0 9.1 9.2 9.3 9.4 9.5 H.C. Ohanian, J.T. Markert (2007). Physics for Engineers and Scientists. 1 (3rd ed.).
- ↑ Wolfram MathWorld - Coordinates.
- ↑ Knudsen, Jens M.; Hjorth, Poul (2012). Elements of Newtonian Mechanics (illustrated ed.). Springer Science & Business Media. p. 30.
- ↑ Charleton, Walter, 1654, Physiologia Epicuro-Gassendo-Charltoniana: or a Fabrick of Science Natural Upon the Hypothesis of Atoms, London: Tho. Newcomb. Reprinted with indices and introduction by Robert Hugh Kargon, New York and London: Johnson Reprint Corporation, 1966.
- ↑ 13.0 13.1 Tom Henderson. "Describing Motion with Words". The Physics Classroom.
- ↑ Jesseph, Douglas M. (1998). "Leibniz on the Foundations of the Calculus: The Question of the Reality of Infinitesimal Magnitudes". Perspectives on Science. 6.1&2: 6–40. Retrieved 31 December 2011.
- ↑ 15.0 15.1 15.2 15.3 Wilson, Edwin Bidwell (1901). Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. p. 125.
- ↑ 16.0 16.1 Relative Velocity. Isaac Physics.
- ↑ 17.0 17.1 Bondi, Hermann (1980). Relativity and Common Sense. Courier Dover Publications. pp. 3.
- ↑ Lehrman, Robert L. (1998). Physics the Easy Way. Barron's Educational Series. pp. 27.
- ↑ Donald T Greenwood (1997). Classical dynamics (Reprint of 1977 edition by Prentice-Hall ed.). Courier Dover Publications. p. 313.
- ↑ 20.0 20.1 Edwin F. Taylor and John Archibald Wheeler, Spacetime Physics, 2nd ed. (Freeman, NY, 1992)
- ↑ Moulton, F. R. (1970). An introduction to celestial mechanics. Courier Corporation.
- ↑ Goldstein, Herbert (1980). Classical mechanics (2nd ed.). Reading, Mass.: Addison-Wesley Pub. Co.
- ↑ The Physics Classroom - Momentum.
- ↑ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2005). The Feynman lectures on physics, Volume 1: Mainly Mechanics, Radiation, and Heat (Definitive ed.). San Francisco: Pearson Addison-Wesley. Ch. 9.
- ↑ Lanczos, Cornelius (1970). The Variational Principles of Mechanics. Toronto: University of Toronto Press.
- ↑ 26.0 26.1 26.2 Reif, F. Understanding Basic Mechanics 2, illustrated. Wiley: pp. 95, 1995.
- ↑ Ruina, Andy; Pratap, Rudra (2002). Introduction to Statics and Dynamics. Oxford University Press. pp. 79-105.
- ↑ Puri, Avinash (1996). "The Art of Free-body Diagrams". Physics Education. 31 (3): 155.
- ↑ Edlich, R. F., Kelley, A. R., Morton, K., Gellman, R. E., Berkey, R., Greene, J. A., ... & Long III, W. B. (2010). A case report of a severe musculoskeletal injury in a wheelchair user caused by an incorrect wheelchair ramp design. The Journal of emergency medicine, 38(2), 150-154.
- ↑ Movement means energy 互聯網檔案館嘅歸檔,歸檔日期2018年1月6號,..
- ↑ Naito, K., Takagi, H., & Maruyama, T. (2011). Mechanical work, efficiency and energy redistribution mechanisms in baseball pitching. Sports Technology, 4(1-2), 48-64.
- ↑ Conservative Force. HyperPhysics.
- ↑ What is kinetic energy?.
- ↑ Derivation of the Kinematics Equation.
- ↑ Bernoulli's Equation & Applications Of Bernoulli's Equation 互聯網檔案館嘅歸檔,歸檔日期2020年3月16號,..
- ↑ What is gravitational potential energy?.
- ↑ Pendrill, A. M., Karlsteen, M., & Rödjegård, H. (2012). Stopping a roller coaster train. Physics Education, 47(6), 728.
- ↑ Shaw, S. W., & Haddow, A. G. (1992). On 'roller-coaster' experiments for nonlinear oscillators. Nonlinear Dynamics, 3(5), 375-384.
- ↑ 39.0 39.1 39.2 Halliday, D.; Robert R., Jearl Walker. Fundamental of Physics, 7th Ed. USA: John Wiley and Sons, Inc., 2005.
- ↑ Galili, I.; Tseitlin, M. Newton's First Law: Text, Translations, Interpretations and Physics Education. Science & Education. 2003, 12 (1): 45–73.
- ↑ O'Sullivan, C. Newton's laws of motion: Some interpretations of the formalism. American Journal of Physics. Feb 1980, 48 (2): pp. 131.
- ↑ 42.0 42.1 C. Hellingman. Newton's third law revisited. Phys. Educ, 1992, 27 (2): 112–115.
- ↑ - Proposition 75, Theorem 35: p.956 - I. Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton's Principia, by I.Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4
- ↑ Isaac Newton: "In [experimental] philosophy particular propositions are inferred from the phenomena and afterwards rendered general by induction": "Principia", Book 3, General Scholium, at p.392 in Volume 2 of Andrew Motte's English translation published 1729.
- ↑ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006". Reviews of Modern Physics. 80 (2): 633–730.
- ↑ Ugural, A. C.; Fenster, S. K. (2003). Advanced Strength and Applied Elasticity (4th ed.). Prentice-Hall.
- ↑ Beiser, A. (2003). Concepts of modern physics. Tata McGraw-Hill Education.
- ↑ 48.0 48.1 Wolfgang Rindler (1991). Introduction to Special Relativity (2nd ed.), Oxford University Press.
- ↑ Relativistic Momentum. HyperPhysics.
- ↑ 50.0 50.1 Feynman, R., QED: The Strange Theory of Light and Matter, Penguin 1990 Edition, p. 84.
- ↑ Tipler, Paul A. and Ralph A. Llewellyn (2003). Modern Physics. 4th ed. New York; W. H. Freeman and Co. pp. 203–4, 222–3, 236.
- ↑ Beer, F.P. & Johnston Jr, E.R. (1992). Statics and Mechanics of Materials. McGraw-Hill, Inc.
- ↑ Asai, T., Seo, K., Kobayashi, O., & Sakashita, R. (2007). Fundamental aerodynamics of the soccer ball. Sports Engineering, 10(2), 101-109.
- ↑ Edmund Taylor Whittaker (1904). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies. Cambridge University Press. Chapter 1.
- ↑ Batra, R. C. (2006). Elements of Continuum Mechanics. Reston, VA: AIAA.
- ↑ Gibbs, Josiah Willard (1902). Elementary Principles in Statistical Mechanics. New York: Charles Scribner's Sons.
除咗上邊呢啲文,仲可以進一步閱讀:
- Feynman, Richard; Phillips, Richard (1998). Six Easy Pieces. Perseus Publishing. ISBN 978-0-201-32841-7.
- Goldstein, Herbert; Charles P. Poole; John L. Safko (2002). Classical Mechanics (3rd ed.). Addison Wesley. ISBN 978-0-201-65702-9.
- Kibble, Tom W.B.; Berkshire, Frank H. (2004). Classical Mechanics (5th ed.). Imperial College Press. ISBN 978-1-86094-424-6.
- Kleppner, D.; Kolenkow, R.J. (1973). An Introduction to Mechanics. McGraw-Hill. ISBN 978-0-07-035048-9.
- Morin, David (2008). Introduction to Classical Mechanics: With Problems and Solutions (1st ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-87622-3.
- Gerald Jay Sussman; Jack Wisdom (2001). Structure and Interpretation of Classical Mechanics. MIT Press. ISBN 978-0-262-19455-6.
- O'Donnell, Peter J. (2015). Essential Dynamics and Relativity. CRC Press. ISBN 978-1-4665-8839-4.






































































































































