 一啲繩嘅振動
一啲繩嘅振動
當正弦波經過一條繩嘅時候,條繩上面每一點都會進行簡諧振動,然後條繩就可以產生音調。但係,有一條更加重要嘅公式,係關於嗰條正弦波嘅波速。假設嗰條繩嘅(水平)張力係  ,每單位長度嘅質量係
,每單位長度嘅質量係  ,咁經過嗰條繩嘅正弦波嘅波速
,咁經過嗰條繩嘅正弦波嘅波速  係:
係:

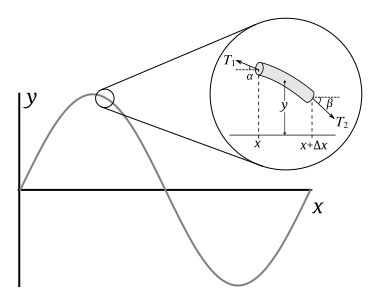 Illustration for a vibrating string
Illustration for a vibrating string
睇下右面嘅圖。假設攞一橛好短嘅線段(咁樣成橛繩都可以當做同一個粒子),水平嚟計嘅長度係  (或者可以寫做
(或者可以寫做  ,參考差動)。
,參考差動)。
考慮響距離  呢度嘅斜率,同埋力嘅分解,得到:
呢度嘅斜率,同埋力嘅分解,得到:

考慮響距離  呢度嘅斜率,同埋力嘅分解,得到:
呢度嘅斜率,同埋力嘅分解,得到:

但係,根據波嘅定義,因為波嘅其中一個特性係剩係會傳播能量,而唔會傳播任何物質,所以係條波經過嘅地方,每一個粒子都只會上下咁振,而永遠唔會有水平方向嘅位移,再根據牛頓第一定律,得到:

於是,就可以得到:


考慮垂直方向嘅淨力:

只不過,根據牛頓第二定律:

於是:


左邊嗰嚿嘢其實係二階偏導數  ,即係
,即係  。得到:
。得到:

而根據波動方程, 。所以:
。所以:

經過整理,得到  。
。
如果想要嚴格啲嘅證明,可以用正弦波嘅函數表示公式:

咁樣以上得到嘅偏微分方程就會變成:

約走個正弦波函數表示公式再執靚佢,得到:

但係因為  ,所以條式變咗:
,所以條式變咗:

所以, 。
。






























