加速度
| 加速度 | |
|---|---|
 喺真空(冇空氣阻力嘅情況),畀地球吸引嘅物件會以一個穩定嘅速度加快。 | |
Common symbols | a |
| SI unit | m/s2, m·s−2, m s−2 |
Derivations from other quantities | |
| Dimension | |

喺力學入面,「加速度」係一個物體嘅速度隨時間嘅變化率。加速度係運動學嘅幾個組成部分之一,運動學係研究運動嘅學科。加速度係向量量(即係佢哋有大小同方向)。[1][2]一個物體嘅加速度方向由作用喺嗰個物體上嘅「淨」力嘅方向決定。根據牛頓第二定律,[3]一個物體嘅加速度大小係由兩個原因共同影響:
舉例嚟講,當一架車輛由靜止狀態(喺慣性參考系中速度為零)開始,沿直線以越嚟越快嘅速度行駛,佢就係喺行駛方向加速。如果車輛轉彎,就會向新方向產生加速度,改變佢嘅運動向量。車輛喺當前運動方向上嘅加速度叫做線性加速度(或者喺圓周運動中叫做切向加速度),車上嘅乘客會感受到一股將佢哋推向座位背嘅力。當改變方向時,產生嘅加速度叫做徑向加速度(或者喺圓周運動中叫做向心加速度),乘客會感受到一種離心力。如果車輛嘅速度減慢,呢個就係一個方向同速度向量相反嘅加速度(數學上係一個負數,如果運動係單向嘅而且速度係正數),有時叫做「減速」[4][5]或者「延遲」,乘客會感受到減速嘅反應力,表現為一股將佢哋向前推嘅慣性力。喺太空船入面,呢啲負加速度通常係通過燃燒逆推火箭嚟實現嘅。[6]加速同減速嘅處理方式係一樣嘅,因為佢哋都係速度嘅變化。乘客會感受到呢啲加速度(切向、徑向、減速),直到佢哋相對於速度變化嘅加速度嘅相對(差分)速度喺參考系中變為零為止。
定義同特性
[編輯]
平均加速度
[編輯]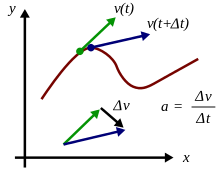
一個物體喺一段時間內嘅平均加速度係佢嘅速度變化量 除以呢段時間嘅長度 。用數學表示就係:
瞬時加速度
[編輯]
- 加速度函數 a(t);
- 加速度嘅積分係速度函數 v(t);
- 而速度嘅積分係距離函數 s(t).
瞬時加速度係一個無窮小時間間隔內平均加速度嘅函數極限。用微積分嚟講,瞬時加速度係速度向量對時間嘅導數: 因為加速度定義為速度 v 對時間 t 嘅導數,而速度又定義為位置 x 對時間嘅導數,所以加速度可以理解為 x 對 t 嘅二階導數:
(喺呢度同其他地方,如果係直線運動,方程式入面嘅向量可以用純量代替。)
根據微積分基本定理,可以睇到加速度函數 a(t) 嘅積分就係速度函數 v(t);即係話,加速度對時間(a 對 t)圖嘅曲線下面嘅面積就相當於速度嘅變化。
同樣,加加速度函數 j(t)(即加速度函數嘅導數)嘅積分可以用嚟計算某個時間嘅加速度變化:
單位
[編輯]加速度嘅量綱係速度(L/T)除以時間,即 L T−2。加速度嘅SI單位係米每平方秒(m s−2);或者叫做「米每秒每秒」,因為每秒鐘速度以米每秒為單位嘅變化量等於加速度值。
其他形式
[編輯]一個做圓周運動嘅物體——好似圍繞地球運行嘅衞星——因為運動方向嘅改變而加速,雖然佢嘅速率可能係恆定嘅。喺呢種情況下,我哋話佢經歷緊「向心」(指向圓心)加速。
固有加速度,即一個物體相對於自由落體狀態嘅加速度,係用一種叫做加速度計嘅儀器嚟測量嘅。
喺經典力學中,對於質量恆定嘅物體,物體質心嘅(向量)加速度同作用喺佢身上嘅淨力向量(即所有力嘅和)成正比(牛頓第二定律): 其中 F 係作用喺物體上嘅淨力,m 係物體嘅質量,而 a 係質心嘅加速度。當速度接近光速嘅時候,相對論效應會變得越嚟越大。
切向加速度同向心加速度
[編輯]
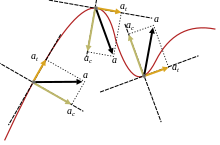
一個粒子喺曲線路徑上運動嘅速度可以寫成時間嘅函數: 其中 v(t) 等於沿路徑運動嘅速率,而 係一個單位切向量,指向所選時刻嘅運動方向。考慮到速率 v(t) 同 ut 方向嘅變化,一個喺曲線路徑上運動嘅粒子嘅加速度可以用兩個時間函數乘積嘅鏈式法則寫成:[7]
其中 un 係粒子軌跡嘅單位(向內)法向量(亦稱為「主法向量」),而 r 係佢喺時間 t 嘅瞬時曲率半徑,基於密切圓。呢兩個分量
分別叫做切向加速度同法向或徑向加速度(喺圓周運動中叫做向心加速度,請參見圓周運動同向心力)。
三維空間曲線嘅幾何分析,解釋咗切向量、(主)法向量同副法向量,由弗萊內-塞雷公式描述。[8][9]
睇埋
[編輯]引咗
[編輯]- ↑ Bondi, Hermann (1980). Relativity and Common Sense. Courier Dover Publications. pp. 3. ISBN 978-0-486-24021-3.
- ↑ Lehrman, Robert L. (1998). Physics the Easy Way. Barron's Educational Series. pp. 27. ISBN 978-0-7641-0236-3.
- ↑ Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. p. 43. ISBN 978-0-559-36871-4.
- ↑ P. Smith; R. C. Smith (1991). Mechanics (第2nd, illustrated, reprinted版). John Wiley & Sons. p. 39. ISBN 978-0-471-92737-2. Extract of page 39
- ↑ John D. Cutnell; Kenneth W. Johnson (2014). Physics, Volume One: Chapters 1-17, Volume 1 (第1st0, illustrated版). John Wiley & Sons. p. 36. ISBN 978-1-118-83688-0. Extract of page 36
- ↑ Raymond A. Serway; Chris Vuille; Jerry S. Faughn (2008). College Physics, Volume 10. Cengage. p. 32. ISBN 9780495386933.
- ↑ Weisstein, Eric W. "Chain Rule". Wolfram MathWorld. Wolfram Research. 喺2 August 2016搵到.
- ↑ Larry C. Andrews; Ronald L. Phillips (2003). Mathematical Techniques for Engineers and Scientists. SPIE Press. p. 164. ISBN 978-0-8194-4506-3.
- ↑ Ch V Ramana Murthy; NC Srinivas (2001). Applied Mathematics. New Delhi: S. Chand & Co. p. 337. ISBN 978-81-219-2082-7.















