已解遊戲
閱讀設定

已解遊戲(已經解決咗嘅遊戲)係博弈論同遊戲相關研究上講到嘅一個概念。如果話某隻遊戲係一隻已解遊戲,意思係話喺呢隻遊戲嘅任何一個位,假設兩位玩家都識用同會用最好(令自己贏面有咁大得咁大)嘅策略,觀察者可以完美噉預測結果會係點,即係會完美估到邊個贏定係打和。
類型
[編輯]睇埋:決策樹
- 極弱已解:淨係知道個結果(邊個贏定係打和?),唔知要用咩策略達到嗰個結果。
- 弱已解:由起始狀態開始玩,已經知道結果同策略。
- 強已解:由是但一點開始玩,都會知道結果同策略。
遊戲
[編輯]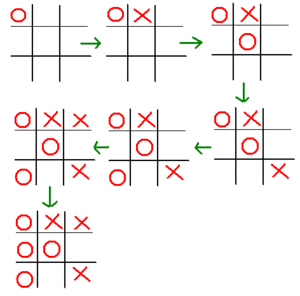
例如井字過三關就係一隻已解遊戲。井字過三關係一隻好簡單嘅遊戲,喺第一步得嗰三個可能性咁少—
- 填中間、
- 填角落(填左上角、填右上角、填左下角同填右下角功能上等同)同
- 填側邊(填左側、填右側、填上側同填下側功能上等同)。
用以下噉嘅策略玩,可以達致包保坐底打和,永遠都唔會輸。想像而家輪到一位玩家填,無論佢係交叉定圓圈都好,佢都要由以下嘅列表度揀位置最高嗰一步嚟行(如果 1 執行唔到,就用 2;如果 2 執行唔到,就用 3... 如此類推)[3]:
- 贏:如果自己已經有兩個符號成一條線,填第三個落去,贏。
- 擋:如果對手已經有兩個符號成一條線,要即刻喺第三個位嗰度填自己符號。
- 兩難:要營造一個局勢,令自己跟住落嚟有兩個贏位(填咗就即贏)可以填。
- 擋兩難:如果對手下一步可以製造一個兩難,自己就要郁手阻擋佢個兩難;擋兩難嘅一個特殊情況係,如果自己霸住中間而對手霸咗兩隻相反嘅角(即係對手霸咗左上右下或者左下右上),自己填角落會即輸,應該要填側邊。
- 填正中央。
- 填同對手相反嘅角落。
- 填角落。
- 填側邊。
好似井字過三關噉嘅遊戲,算係強已解。
解法
[編輯]内文:窮舉搜尋
要達致弱已解或者強已解,最簡單直接嘅方法係窮舉搜尋[2]:窮舉搜尋係演算法一類,泛指靠住「將啲可能性逐個逐個攞嚟睇」解決問題嘅演算法;呢種做法可以輕易噉解決一啲簡單嘅遊戲—例如井字過三關噉,井字過三關喺第一步得三個可能性,而可能性少就表示,電腦唔使嘥好多工夫就可以睇勻晒所有可能性。相比之下,國際象棋淨係第一步白棋行嗰刻已經有 20 個可能性咁多,而跟住落嚟可能性嘅數量會有爆發性嘅增長,喺十步之前已經會超過 100 萬個可能性[註 1],廿一世紀初嘅電腦仲未有足夠嘅運算能力,做唔到「將咁多個可能性逐個逐個攞嚟睇,喺合理咁短嘅時間內畀答案」。
睇吓
[編輯]文獻
[編輯]- Jäger, F. (2019, April). Checkers Solved (PDF). In Seminar: Artifical Inelligence for Games.
- Schaeffer, J., Burch, N., Bjornsson, Y., Kishimoto, A., Muller, M., Lake, R., ... & Sutphen, S. (2007). Checkers is solved (PDF). Science, 317(5844), 1518-1522.
註釋
[編輯]引咗
[編輯]以下係文中用咗嘅重要概念嘅英文名:
- 已解遊戲:solved game
- 極弱已解:ultra-weakly solved
- 弱已解:weakly solved
- 強已解:strongly solved
- 窮舉搜尋:brute-force search
- ↑ 1.0 1.1 Jäger, F. (2019, April). Checkers Solved (PDF). In Seminar: Artifical Inelligence for Games.
- ↑ 2.0 2.1 Allis, Louis Victor (1994-09-23). Searching for Solutions in Games and Artificial Intelligence (PhD thesis). Maastricht: Rijksuniversiteit Limburg.
- ↑ Kevin Crowley, Robert S. Siegler (1993). "Flexible Strategy Use in Young Children's Tic-Tac-Toe". Cognitive Science. 17 (4): 531-561. 佢個 Table 1 講咗以下嘅技巧。

