資訊熵
資訊熵(粵拼:zi1 seon3 soeng1 | 英文:information entropy)係資訊理論(研究資訊嘅數學理論)上嘅核心概念。同物理學上所講嘅熵唔同,資訊論當中嘅「熵」係一個指標,用嚟量度一個有隨機性喺入面嘅變數或者過程當中帶有幾多不確定性喺入面[1]。
舉個例說明,想像家吓掟一個銀仔同擲一粒骰仔,假設個銀仔同粒骰仔係冇出千嘅,前者有 50% 機會率係公、50% 機會率係字,而後者有 1/6 機會係擲到「1」、1/6 機會係擲到「2」... 如此類推,即係話[註 1]:
- 掟銀仔( 表示掟銀仔結果;0 代表公、1 代表字):
- 擲骰仔( 表示擲到嘅數字):
後者嘅情況有更加高嘅資訊熵-後者當中有更多嘅可能性喺度,所以不確定性亦都更加大。亦都因為噉,「話俾人知掟銀仔嘅結果」所俾嘅資訊少過「話俾人知擲骰仔嘅結果」所俾嘅,因為喺後者情況當中,「提供資訊」所消除嘅資訊熵更加多。就係噉,資訊論做到將「資訊」呢一個概念量化,令到資訊成為一個喺科學上可以被研究嘅對象[1][2]。
以下嘅內容係建基於概率論嘅基礎概念嘅。
算式
[編輯]俾是但一個變數,佢會有一啲可能數值,例如「某年某月某日某刻掟某一個銀仔」嘅可能數值大致上有兩個-「公」同「字」。每個數值都會有一定嘅機會率出現,而描述每一個可能數值出現嘅機會率嘅就係所謂嘅概率質量函數(probability mass function)。知道咗某一件事件嘅概率質量函數之後,件事件所帶有嘅資訊熵(數學符號係 ,單位係山農)可以用以下呢條式計算[1]:
- ;
喺呢條式當中, 係指第 i 個可能性發生嘅機會率,而 係 以 2 做基數嘅對數。成條式用日常用語講嘅話如下:「考慮一件事件嘅所有可能性,將每一個可能性嘅機會率乘嗰個可能性嘅機會率以 2 做基數嘅對數,再將呢啲得出嘅數加埋嗮一齊,再將個數負向,就會得出件事件所包含嘅資訊熵」。用呢條式計嘅話,「掟一粒冇出千嘅銀仔」(即係話「公」同「字」嘅機會率都係 50%)呢件事件當中帶嘅資訊熵()係[3]:
- ;
喺直覺上,呢條式係喺度量度緊件事件含有嘅不確定性。科學家之所以會揀用呢條式嚟計資訊熵,係因為喺可能嘅算式當中,得呢條符合佢哋心目中「一條計不確定性嘅算式應有嘅特性」:例如一件肯定嘅事件係理應冇資訊熵嘅-而如果其中一個可能性機會率等如「1」(即係其他可能性機會率冚唪唥等如「0」), 呢條式會俾出「0」;而另一方面,喺每個可能性機會率都一樣(不確定性最大化)嗰陣, 俾嘅數值會最大化[4]。
概論
[編輯]- 資訊熵嘅單位係位元(bit)。有啲研究者會用 2 以外嘅數做上面條式個對數嘅基數嘅,不過道理都一樣,例如用 28 = 256 做基數嘅話,條式就會俾出以位元組(byte)作為單位嘅資訊熵[5]。
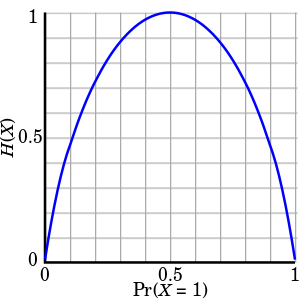
- 資訊熵算式嘅一個特殊情況涉及一個得兩個可能數值嘅隨機變數,例如「掟銀仔嘅結果」就屬於呢種變數。喺呢個情況下,兩個可能性嘅機率加埋實會等如 1(,當中 同 係兩個可能情況分別嘅機率),而呢件事件條資訊熵式就係所謂嘅二元熵函數。條式係噉樣嘅:
- -係將 應用落去「得兩個可能性」嘅情況嘅樣。
- 想像家吓有一個資訊源,佢傳送一連串有 N 個符號嘅資訊,而每個符號都係獨立同分佈(iid)-指一個符號係乜唔會影響嗰串嘢入面第啲符號係乜,但每個符號嘅概率分佈相同,例如一連串互不相干,每個都係隨機噉揀嘅英文字母-呢串嘢嘅資訊熵係 (當中 係每一個個別符號嘅資訊熵)咁多位元;而如果呢串嘢係同分佈(每個符號概率分佈相同)但係唔獨立(一個符號係乜可以影響第啲符號係乜嘅機率)-例如係一篇用英文寫嘅文章噉,如果佢某一橛係「information」呢個字嘅話,噉呢橛嘅下一格好大可能係一個空位-喺呢種情況下,串嘢嘅資訊熵會細過 。
- 如果有個人傳遞 1,000 位元(0 同 1)長嘅數碼訊號,而收訊號嗰個人喺訊號傳出去之前經已完全噉知道嗮每一個位元係「1」定「0」,噉傳訊號嗰個人冇傳達到任何新資訊-因為收訊號嗰個人喺收到訊號前後嘅資訊熵都係「0」,所以呢串訊號嘅傳遞並冇消除任何資訊熵。但如果喺收訊號嗰個人眼中嗰 1,000 個位元每一個都係 50% 機率係「1」、50% 機率係「0」嘅話,噉用 嚟計,佢透過接收呢串訊號會收到 1,000 位元嘅資訊。
註釋
[編輯]睇埋
[編輯]文獻
[編輯]- Cover, T.M., Thomas, J.A. (2006), Elements of Information Theory - 2nd Ed., Wiley-Interscience, ISBN 978-0-471-24195-9
- MacKay, D.J.C. (2003), Information Theory, Inference and Learning Algorithms, Cambridge University Press, ISBN 978-0-521-64298-9
- Arndt, C. (2004), Information Measures: Information and its Description in Science and Engineering, Springer, ISBN 978-3-540-40855-0
引用
[編輯]- ↑ 1.0 1.1 1.2 Demystifying Entropy. Towards Data Science.
- ↑ Fazlollah M. Reza (1994) [1961]. An Introduction to Information Theory. Dover Publications, Inc., New York.
- ↑ Fazlollah M. Reza (1994) [1961]. An Introduction to Information Theory. Dover Publications, Inc., New York.
- ↑ Gray, R. M. (2011), Entropy and Information Theory, Springer.
- ↑ Norman Abramson (1963), Information theory and coding. McGraw-Hill.






![{\displaystyle [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83021ecdd7307a04dbb7873affcaac031e7e935a)











