歐幾里得幾何
閱讀設定

歐幾里得幾何,又叫歐氏幾何、歐式幾何、平面幾何,係古希臘數學家歐幾里得《幾何原本》入面講嘅幾何學,涉及二維平面上嘅幾何。
公理
[編輯]睇埋:幾何原本
响佢本名著《幾何原本》裏面,歐幾里得提出咗五條公理,以「假設咗呢五條公理係真確」做前提嚟諗幾何學[1]:
- 是但搵兩點 同 嚟睇,嗰兩點之間都可以有條獨一無二嘅直線將兩點連接埋一齊。
- 一條直線(最少理論上)可以無限噉延長。
- 有咗「圓心」同「直徑」呢兩樣資訊,就可以建構一個圓形。
- 所有嘅直角冚唪唥都係一個板嘅。
- 平行公設(parallel postulate):是但搵條線 同點 ,當中 唔喺 上面,都實會有一條獨一無二嘅直線會係通過 得嚟又唔會同 相交嘅-即係話呢條線同 平行。而如果兩條線之間唔係平行,噉兩條線無限延長最後實會令到兩條線相交(好似下圖噉)。
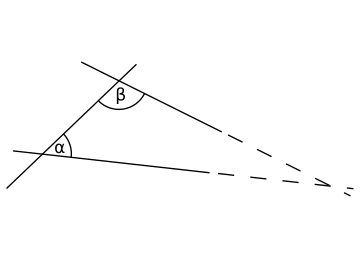
然後歐幾里得就攞住呢五條公理、用數學證明嘅方法證明嗮當時已知嘅幾何學定理。喺歐幾里得之後,仲有數學家試過對呢拃公理嘅具體定義作出修改-即係將條公理嘅定義改做比較清楚易明嘅形式,但改前改後拃公理都係可以攞嚟證明已知嘅幾何定理嘅。
睇埋
[編輯]攷
[編輯]- ↑ Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications. In 3 vols.: vol. 1







