生還分析

生還分析(粵拼:sang1 waan4 fan1 sik1;英文:survival analysis),又可以譯做生存分析,係一套統計分析技術。喺最基本上,生還分析係醫學用嘅,專門攞嚟分析患咗重病(例如癌症)慢慢趨向死亡嘅病人「會有幾耐命」[1]。醫學研究者可以攞住啲病人數據,入落電腦度計生還分析嘅數,解答以下呢啲問題[2]:
由統計學層面睇嘅話,生還分析仲有得廣義化,研究死亡以外嘅「終結事件」:例如遊戲製作領域,就有以「玩家放棄隻遊戲或者產品唔再返嚟玩」做想像中嘅終結事件,剖析啲玩家點樣隨時間對隻遊戲失去興趣最後放棄隻遊戲,想搵出有乜因素會影響一位玩家玩幾耐先放棄[5];除此之外,生還分析仲有喺市場學度畀人攞嚟分析顧客保留(分析啲客點樣隨時間對隻產品失去興趣,最後放棄隻產品)[6],又有喺工程學上畀人攞嚟做預測式維修(估計啲機械同機件點樣隨時間開始有故障,最後壞嗮)[7]... 呀噉。
基本概念
[編輯]响狹義上,生還分析係[2]:Ch. 1.1
| 「 | 」 |
舉個簡單例子:想像家吓有位癌症研究者想研究某隻肝癌;佢想知解答「有邊啲因素會影響病人生存到幾耐?」呢條問題,於是佢就去搵咗大拃醫療數據(input)返嚟,啲數據描述咗 500 位有嗰隻肝癌嘅病人,包括每位病人生存咗幾耐,以及嗰位病人嘅各種因素(簡單嘅有性別同年紀)呀噉;跟住佢可以將啲數據畫做圖,當中
得出下圖噉嘅圖。

最基本嗰隻生還分析做嘅,就係(用電腦)計大拃數,務求搵出[8][9]
- 啲病人生存幾耐,同埋
- 研究者指定嘅因素
兩者之間有乜關係(output),例如指定嘅因素係「受咗邊隻療法」-想像將病人分「接受咗療法 A 嘅病人」同「接受咗療法 B 嘅病人」兩組,同兩組各自噉畫條線,研究者可以靠住生還分析計嘅數比較兩條線(詳情可以睇下面 log-rank 測試),得知「接受咗療法 A 嘅病人,會唔會生存得耐過接受咗療法 B 嗰啲?」噉嘅資訊。呢啲研究會幫到醫療工作者思考點樣更有效噉照料同醫啲病人[1]。
篇文以下嘅內容會講「生還分析計嗰啲數」嘅詳情。
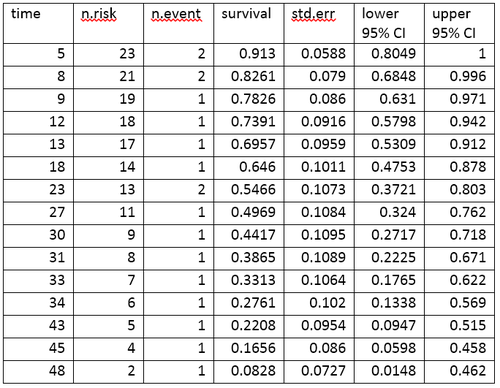
time:有最少一件終結事件(死亡)發生嗰啲時間點;
n.risk:嗰點時間到之前嗰剎那「有風險嘅個體」嘅數量,當中「有風險」係指嗰個個體仲未經歷終結事件,而且响嗰個時間點之前或者嗰時冇出現刪失(睇下面);
n.event:嗰點時間有幾多個個體經歷終結事件;
survival:淨低幾多 % 嘅個體未經歷終結事件;
std.err:估計生還率嘅標準誤差;CI:信心區間。
刪失現象
[編輯]刪失[e 4]係做生還分析成日會撞到嘅問題,指「起始或者終結事件發生嘅時間點唔明確」嘅情況:想像家陣研究者又係想研究班肝癌病人生存到幾耐,佢搵咗班病人返嚟,响跟住嗰一年之間跟進佢哋嘅病情,但可能嗰隻肝癌致命性唔係咁高,有好多病人過咗一年之後都未死,而且有啲仲好返,甚至好返之後移民去第度,搞到研究者冇辦法繼續跟進佢哋;噉即係話有部份病人嘅死亡時間(終結事件發生時間)係不詳[10]。
例如想像下圖:下圖 X 軸做時間 Y 軸病人;病人有 5 位,頭嗰 4 位响研究結束前死咗[e 5],但最後嗰位去到研究做完[e 6]嗰陣都仲未死。

數學化啲噉講,刪失可以噉諗:想像 係個隨機變數,表示「距離死亡仲有幾耐」,而 係個隨機變數,表示「距離引致刪失嗰件事件(份研究結束)仲有幾耐」,研究者觀察得到嗰個時間數值 實際上係[2]:Ch. 1.3
嘅數值一係 1 一係 0,表示「有冇刪失發生」呢樣資訊。
順帶一提,刪失仲可以進一步細分做幾種:好似上述呢種「終結事件發生時間不明」嘅情況,就係所謂嘅右刪失-如果將時間畫做線(好似上面幅圖噉),左邊做過去右邊做未來,噉死唔去嗰啲病人嘅生存時間條線「最右去到邊」唔知;相對於右刪失嘅係左刪失-左刪失相對少見啲,指「起始事件發生時間不明」,例如可能想像一個醫療技術上冇咁先進嘅國家,對啲國民嘅健康狀態監察得唔夠嚴謹,搞到有啲病人係「唔知佢具體係幾時患咗隻病」嘅,頂攏淨係知啲病人係「幾時確診知佢有隻病」[11][12]。
統計模型
[編輯]
生還函數基礎
[編輯]生還函數([e 9] )係生還模型入面最基本嗰個函數,負責定義「生存得到超過 咁耐」嘅機率[註 1]。數學化啲講即係[2]:Ch. 2.1:
嘅數值
- 响一開始嗰陣係 1,
- 然後會慢慢噉跌,最後變成接近 0 嘅數值,
- 但永遠唔會變成負數。
另一個重要特徵係永遠唔會升-因為生還分析本質上就係模擬緊啲慢慢噉趨向終結事件(例如慢慢噉趨向死亡)嘅現象,即係[13]
-而呢句嘢講嘅,係生還分析最重要嘅特徵之一。响實際應用上,啲人好多時會設定生還函數係指數函數[14]、威布分佈[e 10]或者伽瑪分佈[e 11]呀噉-呢啲函數簡單講就係以唔同方式「慢慢下跌」嘅線;例如指數函數望落會係噉嘅樣:
係個參數。隨住 數值升, 數值會慢慢跌。
生還函數進階
[編輯]進一步噉分析生還函數嘅話:
- 危機函數([e 12] ):指以下嘅函數[2]:Ch. 2.1 [註 2]:
- 生還函數可以變少少,變成累計風險函數[e 14][2]:Ch. 2.2 [註 3]:
- ;用日常用語講,累計風險函數表示「死咗人總數升得有幾快」。
- 生還函數可以用積分,提供埋生還時間嘅期望值 [2]:Ch. 2.3 [註 3]:
- 用日常用語講, 反映咗「『生存 咁耐時間嘅機率乘埋 』、『生存 咁耐時間嘅機率乘埋 』... 如此類推加埋」,反映咗「是但搵個個體嚟睇,預佢會生存到幾耐」呢樣資訊。
... 呀噉。
模型建立
[編輯]
Y 軸做 而 X 軸做時間;
紅線表示觀察到嘅數據,
十字表示刪失嘅發生點,
虛線表示 95% 信心區間。
攞住啲數據,研究者就要建立模型,喺實際應用上即係要叫電腦計大拃數,估計個模型嘅參數嘅值,即係搵出例如 入面嗰個 係乜數值。然後研究者知道咗 等參數嘅估計值,就可以(例如)第時用嚟估算有同一隻病嘅病人會有幾耐命[16]。
生還模型同第啲統計模型一樣,參數數值可以攞最佳化演算法建立,即係將個生還函數設定做指數函數、威布分佈或者伽瑪分佈等能夠模擬「某個數值慢慢噉減少」嘅函數,再用最大似然估計(MLE)估 等嘅模型參數嘅值[2]:Ch. 2.6;不過生還分析又有 K-M 估計量等佢專用嘅模型建立方法。
K-M 估計量
[編輯]K-M 估計量[e 15]係種用嚟估計生還函數嘅非參數做法,亦係廿一世紀初最廣受採用嗰種估計生還函數做法[17]。
首先,K-M 估計量假設咗[18]:
- 响是但一個時間點,因為刪失而睇唔到嘅個體,生還機率同仲睇到嗰啲個體一樣。
- 無論一個個體早定遲加入,佢嘅生還機率都一樣。
- 呢點响實際研究上未必成立-例如隻病唔係咁致命,所以啲病人多數都起碼仲有幾年命,而可能份研究進行到半路,有人開發咗隻新療法能夠有效噉醫隻病,噉遲加入嘅個體生還機率明顯高過早加入嗰啲[19]。
- 件終結事件响探測到佢嗰個時間點發生。
- 响實際應用上,呢點都係可以有問題-想像家陣每隔 咁耐就睇個病人一次,响時間點 發現佢死咗,佢真實死亡時間 嚴格上理應係
- 响實際應用上,呢點都係可以有問題-想像家陣每隔 咁耐就睇個病人一次,响時間點 發現佢死咗,佢真實死亡時間 嚴格上理應係
不過當住呢三個假設成立先,「生存到時間點 嘅機率」可以用條件概率噉嘅方式計:「生存到時間點 嘅機率」係「生存過時間點 1 嘅機率」乘「已知生存過時間點 1,生存過時間點 2 嘅機率」... 如此類推,數學化啲講即係話响最基本嗰隻 K-M 估計量之下[20][註 4]:
當中 係指時間點 嗰陣嘅個體總數,而 係指時間點 嗰陣嘅死亡人數;研究者跟手仲有得計埋每個時間點嘅 嘅信心區間[18][21]。
模型比較
[編輯]
响實際應用上,研究者好多時都會想知「呢個呢個因素(自變數)會唔會影響生還時間(應變數)」噉嘅資訊。想像家陣有位研究者,佢想做研究搵方法改善對某隻癌症嘅治療法,尤其係想睇吓唔同療法(或者唔同基因[22]-自變數)會點樣影響「病人有幾耐命」(應變數),於是佢就搵咗 200 位有嗰隻癌症嘅病人嘅數據返嚟,當中 102 位係接受咗療法 A 而淨低嗰 98 位係接受咗療法 B,佢將啲數據分做兩組-
- 受療法 A 嘅病人,同埋
- 受療法 B 嘅病人,
並且同兩組分別噉畫條生還線(好似附圖噉有兩條線)。然後佢就可以同兩組分別噉做模型建立,得出兩個生還模型(兩條線),最後就要郁手比較兩個生還模型有咩差異-簡化嘅可以想像「療法 A 嗰組嘅生還模型,條線嘅斜率會唔會數值上大啲?」噉嘅思考方式[23][4]。
以上噉嘅諗法,組嘅數量係 3 或者以上嗰陣都啱用。
Log-rank 測試
[編輯]Log-rank 測試係最常用嘅「比較唔同組嘅生還模型」方法之一,佢條基本原理用日常用語講係噉:想像家陣將生還模型上嘅每點時間逐點逐點攞嚟睇,睇吓响嗰點時間當中組 A 嘅 同埋組 B 嘅 - 反映咗「個體有幾大機率會死」;如果 係真確,噉研究者理應會預期[24]
| 「 | 是但攞一點時間嚟睇,兩組嘅 都冇顯著分別。
|
」 |
形式化啲噉講,log-rank 測試要計好似以下噉嘅數[23][24][註 5]:
當中 係組嘅數量, 係指「响組 度實際觀察到嘅終結事件(死亡)發生數量」,而 係指「如果啲組之間冇差異,响組 度會預期觀察到嘅終結事件發生數量」。如果啲組之間差異大,噉 嘅數值理應會大-而且學界仲有套標準,講明 數值要去到幾大,兩組之間先算係「有顯著差異」[25]。
比例危機模型
[編輯]比例危機模型[e 17]係另一種分析「呢啲因素會唔會影響到生還時間」嘅方法:Log-rank 測試一個明顯缺點係淨係分析到「自變數係離散」嘅情況-例如自變數係「接受咗 A 定 B 療法」呀噉;但想像家陣研究者可以想睇吓(例如)個人嘅體重會點樣影響佢嘅生還能力,要用 log-rank 測試嘅話佢就頂攏係可以將啲病人分做「體重高過平均」同「體重低過平均」兩組,然後再行 log-rank 測試比較兩組。比例危機模型就係種畀人認為係先進啲嘅做法,可以攞嚟分析「自變數係連續」嘅情況[26][27]。
用比例危機模型嘅做法如下:首先,攞住個危機函數 ,想像好似噉嘅式[26]-
- ,當中
有咗呢個噉嘅函數,研究者就可以用好似迴歸分析[e 19]噉嘅方法,由數據度估計出啲 嘅值,從而睇吓邊啲 有顯著嘅 (對 有顯著嘅影響)- 數值愈細愈表示相應嗰個 能夠減少終結事件發生嘅機率;相反 數值愈大愈表示相應嗰個 能夠提升終結事件發生嘅機率。
廣義應用
[編輯]响廿一世紀初,生還分析開始畀多個領域嘅研究者廣泛採用。初頭嗰陣,生還分析主要係用响醫療度(尤其係癌症研究[1]),不過事實表明生還分析計嗰啲數仲可以廣義化,變成:
| 「 | 」 |
用呢套廣義諗法,生還分析可以攞嚟分析好多同樣涉及
| 「 | 一拃個體,每個都慢慢噉趨向終結事件
|
」 |
嘅現象。想像下圖:

設 X 軸做時間,Y 軸可以係
- 仲有幾多 % 嘅病人生存緊(癌症研究);
- 仲有幾多 % 嘅人堅持減緊肥(體重管理研究;睇下面);
- 仲有幾多 % 嘅客有買同用隻產品(顧客保留研究;睇下面);
- 仲有幾多 % 嘅維基人依然有編輯緊維基(維基友研究;睇下面);
- 仲有幾多 % 嘅機械機件未壞(睇埋可靠性工程同預測式維修等嘅課題)[7];
... 呀噉。
醫療健康
[編輯]
第二個禮拜:(念咒噉)唔食新地... 唔食新地...
第三個禮拜:咦?點解... 我手上揸住個空嗮嘅新地杯、口入面有陣新地味嘅?
响廿世紀尾橛起,醫學研究就有用生還分析研究癌症以外嘅課題,用「死亡」以外嘅嘢做終結事件,好似係體重管理[e 21]研究噉:响廿一世紀初,癡肥日趨普遍,而癡肥會提升好多種重病-例如心臟病同高血壓呀噉-嘅機率;因為噉,醫療工作者開始關注體重管理(指一系列攞嚟幫人維持健康體重嘅技巧)嘅問題[28],體重管理工作好多時都要求參加者持之以恆噉做某啲嘢,例如
... 呀噉。但實證研究表明,體重管理工作成日遇到「啲參加者做做吓半途而廢」嘅情況,例如有多份廿一世紀初嘅研究試過搵人返嚟做體重管理,發覺淨係頭嗰 6 個月已經有成 50% 咁多嘅參加者放棄咗減肥計劃[29][30];於是有醫學同營養學方面嘅工作者就諗咗條計,想用生還分析[31]-
- 設「放棄減肥」做終結事件;
- 用比例危機模型(睇返上面)等嘅方法,睇吓乜因素會影響「參加者堅持到幾耐至放棄減肥」。
例:2019 年巴西運動減肥研究
- 終結事件:放棄減肥
喺 2019 年,有一班巴西嘅醫療研究者就做咗份研究,想睇吓啲人有幾能夠堅持減肥計劃。呢班研究者搵咗 195 個大人返嚟,參與一個 6 個月咁長嘅減肥計劃,(簡化講)要佢哋响跟住嗰 6 個月內每個禮拜都做指定嘅運動,同時參加者有權响任何一點時間宣布放棄,班研究者[31]:
- 研究開始前量度咗拃佢哋預咗用嚟做自變數嘅變數,包括參加者嘅年紀同性別;
- 然後佢哋監察住班參加者,知邊位參加者有跟足 6 個月嘅運動計劃、邊位參加者半途而廢、同埋每位半途而廢嘅參加者係响邊點時間宣布放棄嘅;
- 佢哋亦用埋面試研究噉嘅方法,跟進半途而廢嘅參加者,問佢哋點解想放棄(參加者有權揀唔答)。
然後佢哋行生還分析,用 K-M 估計量建立生還模型,再用 log-rank 測試睇吓唔同組(例如唔同性別)之間嘅生還線有冇顯著分別,發現(例如)性別並唔會對「參加者能唔能夠持之以恆」有影響[31]。
市場學
[編輯]市場學工作好關注顧客保留[e 22]嘅問題:事實表明,當班客開始買同用一隻產品嗰陣,佢哋往往會隨時間對隻產品慢慢喪失興趣,最後放棄唔再買同用隻產品-例如想像家陣有隻新嘅智能手機型號 Z 吸引到唔少人買,但出咗街 6 個月之後,間企業嘅競爭對手出咗隻更勁嘅型號 Y,於是啲客就開始慢慢噉趨向「唔再買同用 Z,改為買同用 Y」(終結事件)嘅狀態;有關呢種現象,可以睇埋產品生命週期嘅概念[34]。
顧客保留講緊嘅,就係一隻產品有幾能夠長遠噉引啲客買同用[34][35]:
- 出咗街 6 個月後,有幾多 % 嘅客仲買緊用緊隻產品?
- 出咗街 12 個月後,有幾多 % 嘅客仲買緊用緊隻產品?
- 出咗街 18 個月後,有幾多 % 嘅客仲買緊用緊隻產品?
... 如此類推。有市場學報告話,就算顧客保留率只係升咗 5% 咁少,利潤已經可以升成 25 至 85% 咁多[35]:p. 1。因為噉,市場學工作者就想諗方法吸引啲客持續買同用隻產品,於是佢哋就諗到條橋,用生還分析做市場學研究,將終結事件設做「唔再買同用件產品」,剖析有邊啲因素能夠影響啲客會買同用件產品幾耐[36]。

例:2016 年遊戲玩家保留研究
- 終結事件:放棄唔再玩隻遊戲
玩家保留[e 24]係遊戲製作上廣受關注嘅課題:玩家保留指一隻電子遊戲有幾能夠長遠噉引啲玩家一路定時定候返嚟玩-事實經驗表明,當一隻電子遊戲出街嗰陣,好多時會吸引到大拃玩家玩,但玩家會隨時間而慢慢對隻遊戲失去興趣(例如有第隻新遊戲出咗),最後放棄隻遊戲(終結事件);噉即係話,玩家保留分析可以想像成「產品 電子遊戲」嘅顧客保留分析[註 6][37]。例如喺 2016 年,就有班法國嘅研究者做咗份研究,想睇吓著名電子遊戲入面嘅玩家保留會受乜因素影響。佢哋搜集咗描述一班玩家嘅數據返嚟,啲數據紀錄咗啲玩家玩隻遊戲嘅紀錄,班研究者[5]:
研究者發現,(簡化講)玩家响遊戲入面用武器用得愈多,佢哋嘅「生還時間」傾向會愈長。噉亦即係話,電子遊戲工作者可以透過量度玩家响遊戲裏面嘅行為嚟預測佢哋會玩幾耐-而呢點對電子遊戲設計嚟講係樣有用嘅資訊[5]。
維基社群
[編輯]又有人用維基百科做生還分析研究嘅對象。
維基百科係由維基友嘅貢獻形成嘅,所以如果一個語言嘅維基百科要做到內容豐富,就必需要識嗰隻語言嘅人樂意成為維基友同埋積極噉寫文。不過要持續噉寫文,並唔係一件容易嘅事-好多人都覺得寫文好難,而且啲人又傾向會隨時間慢慢喪失對維基百科嘅興趣,最後完全放棄編輯維基(終結事件),例如 2005 年就有統計報告指,搵拃响英文維基百科度寫文嘅維基人,做咗第一次編輯一年後大約得返 40% 嘅人仲有响維基活動,淨低嗰啲冚唪唥影都冇埋[38]。一般嚟講,維基百科工作者希望啲人會持續噉寫文同埋做第啲貢獻,令維基百科持續擴張,所以有興趣想解答好似「有咩因素會令一個人持續長期噉寫文」噉嘅問題。設「停手冇再編輯維基」做終結事件,想像[39]:
- 做咗第一次編輯 6 個月後,有幾多 % 嘅維基人仲有响維基活動?
- 做咗第一次編輯 12 個月後,有幾多 % 嘅維基人仲有响維基活動?
- 做咗第一次編輯 18 個月後,有幾多 % 嘅維基人仲有响維基活動?
噉嘅分析。跟住研究者仲可以用比例危機模型等嘅方法,得知「有咩因素會令一個人持續長期噉寫文」[40]。
例:2012 年英維編輯研究
- 終結事件:停手冇再編輯維基
喺 2012 年,有一班英倫嘅資訊科技研究者就做咗份研究,想知「有咩因素會令一個維基友持續長期噉貢獻維基」。呢班研究者(簡化講)响英維度做隨機抽樣,搵咗 86,468 份數據,每份數據描述一個維基友由「生」去到「死」(死 變到完全冇嗮任何維基活動)之間嘅時間,佢哋攞住呢啲數據[39]:
- 佢哋將生還函數設做威布分佈;
- 用數據計出生還函數啲參數同埋危機函數;
- 再將啲數據畫嗮做圖。
佢哋發現,响「過咗 0-2 個禮拜」或者「過咗 8-20 個禮拜」期間,危機函數數值零舍高-維基人零舍大機率會响呢段期間完全喪失貢獻維基嘅興趣;而初頭每月編輯數高(編輯得密)嘅維基友大機率會「生存得耐」(一路持續貢獻好耐)。研究者亦都提出未來嘅研究可以用比例危機模型等嘅方法,睇吓有邊啲自變數會影響維基人「有幾長命」[39]。
睇埋
[編輯]註釋
[編輯]文獻
[編輯]- Allison, P. D. (2010). Survival analysis (PDF). The reviewer's guide to quantitative methods in the social sciences, 413-425.
- Austin, P. C., Allignol, A., & Fine, J. P. (2017). The number of primary events per variable affects estimation of the subdistribution hazard competing risks model. Journal of clinical epidemiology, 83, 75-84.
- Clark, T. G., Bradburn, M. J., Love, S. B., & Altman, D. G. (2003). Survival analysis part I: basic concepts and first analyses. British journal of cancer, 89(2), 232-238,生還分析嘅入門簡介。
- Emmert-Streib, F., & Dehmer, M. (2019). Introduction to survival analysis in practice. Machine Learning and Knowledge Extraction, 1(3), 1013-1038.
- Goel, M. K., Khanna, P., & Kishore, J. (2010). Understanding survival analysis: Kaplan-Meier estimate. International journal of Ayurveda research, 1(4), 274.
- Kalbfleisch, J. D.; Prentice, Ross L. (2002). The statistical analysis of failure time data. New York: John Wiley & Sons. ISBN 047136357X.
- Lawless, Jerald F. (2003). Statistical Models and Methods for Lifetime Data (2nd ed.). Hoboken: John Wiley and Sons. ISBN 0471372153.
- Moore, D. F. (2016). Applied survival analysis using R (Vol. 473). New York, NY: Springer,呢本書講解嗮生還分析啲基本概念,跟住仲講埋用 R 程式語言做生還分析。
- Ogundimu, E. O., Altman, D. G., & Collins, G. S. (2016). Adequate sample size for developing prediction models is not simply related to events per variable. Journal of clinical epidemiology, 76, 175-182,根據統計學研究,做生還分析比例危機模型嗰陣,EPV-指「終結事件數量 / 自變數數量」嘅比例-起碼要係 10:1,最好去到 20:1 咁高。假設自變數嘅每個可能數值嘅出現機率都有咁上下高。
- Piza, E. L., & Sytsma, V. A. (2022). The impact of suspect resistance, informational justice, and interpersonal justice on time until police use of physical force: A survival analysis (PDF). Crime & Delinquency, 00111287221106947,呢份犯罪學研究剖析「當有人報警嗰陣,到場嘅警察要過幾耐時間先會郁手用武力應付狀況(終結事件 = 在場嘅警察郁手用武力)」。
- Rausand, M.; Hoyland, A. (2004). System Reliability Theory: Models, Statistical Methods, and Applications. Hoboken: John Wiley & Sons. ISBN 047147133X.
引咗
[編輯]- ↑ "... the study of survival times and of the factors that influence them."
- ↑ proportion surviving
- ↑ life table
- ↑ censoring
- ↑ times to failure
- ↑ Termination
- ↑ censoring indicator
- ↑ survival model
- ↑ survival function
- ↑ Weibull
- ↑ Gamma
- ↑ hazard function
- ↑ force of mortality
- ↑ cumulative risk function
- ↑ Kaplan-Meier estimator
- ↑ 所謂嘅 uninformative censoring
- ↑ proportional hazards model / Cox model
- ↑ baseline hazard
- ↑ regression
- ↑ "A key characteristic of survival data is that the response variable is a non-negative discrete or continuous random variable, and represents the time from a well-defined origin to a well-defined event."
- ↑ weight management
- ↑ customer retention
- ↑ product life cycle
- ↑ player retention
- ↑ 1.0 1.1 1.2 Clark, T. G., Bradburn, M. J., Love, S. B., & Altman, D. G. (2003). Survival analysis part I: basic concepts and first analyses. British journal of cancer, 89(2), 232-238.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Moore, D. F. (2016). Applied survival analysis using R 互聯網檔案館嘅歸檔,歸檔日期2022年10月21號,. (Vol. 473). New York, NY: Springer.
- ↑ Paul D. Allison. Survival Analysis. Statistical Horizons.
- ↑ 4.0 4.1 Collett, David (2003). Modelling Survival Data in Medical Research (Second ed.). Boca Raton: Chapman & Hall/CRC.
- ↑ 5.0 5.1 5.2 Allart, T., Levieux, G., Pierfitte, M., Guilloux, A., & Natkin, S. (2016, September). Design influence on player retention: A method based on time varying survival analysis. In 2016 IEEE Conference on Computational Intelligence and Games (CIG) (pp. 1-8). IEEE.
- ↑ Li, S. (1995). Survival analysis. Marketing Research, 7(4), 16.
- ↑ 7.0 7.1 Yang, Z., Kanniainen, J., Krogerus, T., & Emmert-Streib, F. (2022). Prognostic modeling of predictive maintenance with survival analysis for mobile work equipment. Scientific Reports, 12(1), 1-20.
- ↑ Wang, J. H., Changchien, C. S., Hu, T. H., Lee, C. M., Kee, K. M., Lin, C. Y., ... & Lu, S. N. (2008). The efficacy of treatment schedules according to Barcelona Clinic Liver Cancer staging for hepatocellular carcinoma-Survival analysis of 3892 patients. European journal of cancer, 44(7), 1000-1006.
- ↑ De Angelis, R., Capocaccia, R., Hakulinen, T., Soderman, B., & Verdecchia, A. (1999). Mixture models for cancer survival analysis: application to population‐based data with covariates. Statistics in medicine, 18(4), 441-454.
- ↑ Lin, D. Y.; et al. (1997). "Estimating medical costs from incomplete follow-up data". Biometrics. 53 (2): 419-434.
- ↑ Darity, William A. Jr., ed. (2008). "Censoring, Left and Right". International Encyclopedia of the Social Sciences. Vol. 1 (2nd ed.). Macmillan. pp. 473-474. Retrieved 6 November 2016.
- ↑ Richards, S. J. (2012). "A handbook of parametric survival models for actuarial use". Scandinavian Actuarial Journal. 2012 (4): 233-257.
- ↑ Kleinbaum, David G.; Klein, Mitchel (2012), Survival analysis: A Self-learning text (3rd ed.), Springer.
- ↑ Cioffi-Revilla, C. (1984). The political reliability of Italian governments: An exponential survival model. American Political Science Review, 78(2), 318-337.
- ↑ R. Cunningham, T. Herzog, R. London (2008). Models for Quantifying Risk, 3rd Edition, Actex.
- ↑ Altman, D. G. (1991). Analysis of survival times. Practical statistics for medical research, 1.
- ↑ Kaplan, E. L., & Meier, P. (1958). Nonparametric estimation from incomplete observations. Journal of the American statistical association, 53(282), 457-481.
- ↑ 18.0 18.1 Goel, M. K., Khanna, P., & Kishore, J. (2010). Understanding survival analysis: Kaplan-Meier estimate. International journal of Ayurveda research, 1(4), 274.
- ↑ 19.0 19.1 Clark, T. G., Bradburn, M. J., Love, S. B., & Altman, D. G. (2003). Survival analysis part I: basic concepts and first analyses. British journal of cancer, 89(2), 232-238. "Some key requirements for the analysis of survival data"
- ↑ Stalpers, Lukas J A; Kaplan, Edward L (4 May 2018). "Edward L. Kaplan and the Kaplan-Meier Survival Curve". BSHM Bulletin: Journal of the British Society for the History of Mathematics. 33 (2): 109-135.
- ↑ Xie, J., & Liu, C. (2005). Adjusted Kaplan-Meier estimator and log‐rank test with inverse probability of treatment weighting for survival data (PDF). Statistics in medicine, 24(20), 3089-3110.
- ↑ Nagy, Á., Munkácsy, G., & Győrffy, B. (2021). Pancancer survival analysis of cancer hallmark genes. Scientific reports, 11(1), 1-10.
- ↑ 23.0 23.1 Clark, T. G., Bradburn, M. J., Love, S. B., & Altman, D. G. (2003). Survival analysis part I: basic concepts and first analyses. British journal of cancer, 89(2), 232-238. "Nonparametric tests comparing survival"
- ↑ 24.0 24.1 Bland, J. M., & Altman, D. G. (2004). The logrank test. Bmj, 328(7447), 1073.
- ↑ Peto, R., Pike, M., Armitage, P., Breslow, N. E., Cox, D. R., Howard, S. V., ... & Smith, P. G. (1977). Design and analysis of randomized clinical trials requiring prolonged observation of each patient. II. analysis and examples. British journal of cancer, 35(1), 1-39.
- ↑ 26.0 26.1 Lin, D. Y., & Wei, L. J. (1989). The robust inference for the Cox proportional hazards model (PDF). Journal of the American statistical Association, 84(408), 1074-1078.
- ↑ David, C. R. (1972). Regression models and life tables (with discussion). Journal of the Royal Statistical Society, 34(2), 187-220.
- ↑ Ryan, D. H., & Kahan, S. (2018). Guideline recommendations for obesity management. Medical Clinics, 102(1), 49-63.
- ↑ Dishman, R. K. (2001). The problem of exercise adherence: Fighting sloth in nations with market economies. Quest, 53(3), 279-294.
- ↑ Sit, J. W., Chair, S. Y., Hui, S. S., Choi, K. C., Chan, A. W., Wong, E. M., & Cheng, H. Y. (2016). A smartphone-based exercise adherence intervention for people with metabolic syndrome: a feasibility pilot study. The Lancet, 388, S64.
- ↑ 31.0 31.1 31.2 Galvim, A. L., Oliveira, I. M., Martins, T. V., Vieira, L. M., Cerri, N. C., de Castro Cezar, N. O., ... & de Oliveira Gomes, G. A. (2019). Adherence, adhesion, and dropout reasons of a physical activity program in a high social vulnerability context. Journal of Physical Activity and Health, 16(2), 149-156.
- ↑ Landers, P. S., & Landers, T. L. (2004). Survival analysis of dropout patterns in dieting clinical trials. Journal of the American Dietetic Association, 104(10), 1586-1588.
- ↑ Ho, K. S., Nichaman, M. Z., Taylor, W. C., Lee, E. S., & Foreyt, J. P. (1995). Binge eating disorder, retention, and dropout in an adult obesity program. International Journal of Eating Disorders, 18(3), 291-294.
- ↑ 34.0 34.1 Page, M., Pitt, L., Berthon, P., & Money, A. (1996). Analysing customer defections and their effects on corporate performance: the case of Indco. Journal of Marketing Management, 12(7), 617-627.
- ↑ 35.0 35.1 Zhang, G. (2007, September). Customer retention based on BP ANN and Survival Analysis (PDF). In 2007 International Conference on Wireless Communications, Networking and Mobile Computing (pp. 3406-3411). IEEE.
- ↑ Mavri, M., & Ioannou, G. (2008). Customer switching behaviour in Greek banking services using survival analysis. Managerial Finance.
- ↑ Demediuk, S., Murrin, A., Bulger, D., Hitchens, M., Drachen, A., Raffe, W. L., & Tamassia, M. (2018, January). Player retention in league of legends: a study using survival analysis. In Proceedings of the Australasian computer science week multiconference (pp. 1-9).
- ↑ Bryant, S. L., Forte, A., & Bruckman, A. (2005, November). Becoming Wikipedian: transformation of participation in a collaborative online encyclopedia. In Proceedings of the 2005 international ACM SIGGROUP conference on Supporting group work (pp. 1-10).
- ↑ 39.0 39.1 39.2 Zhang, D., Prior, K., & Levene, M. (2012, August). How long do Wikipedia editors keep active? (PDF). In Proceedings of the Eighth Annual International Symposium on Wikis and Open Collaboration (pp. 1-4).
- ↑ Ortega, F., & Izquierdo-Cortazar, D. (2009, May). Survival analysis in open development projects. In 2009 ICSE Workshop on Emerging Trends in Free/Libre/Open Source Software Research and Development (pp. 7-12). IEEE.







![{\displaystyle \delta =I[T_{f}<U]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28fcf9354235c8c98c4456e34f03b3a6a1fd04ff)




































