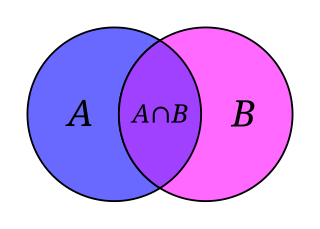
一個典型嘅温氏圖 (Venn diagram);佢顯示咗兩個集合(set)之間嘅交集。 集合論 (粵拼 :Zaap6 hap6 leon6 英文 :set theory),又叫集論 ,係一門研究集合 嘅數學 理論 。佢喺 1870 年代由德國 數學家康托爾 (Georg Cantor)同戴德金 (Richard Dedekind)諗出嚟,而今時今日佢成日都畀數學家 攞嚟做數學基礎 [ 1]
集合
{
1
,
3
,
5
,
7
,
9
,
…
}
{\displaystyle \{1,3,5,7,9,\ldots \}}
呢個集嘅定義 (definition)可以係「所有單數 嘅集」(the set of all odd numbers)⸺一個集可以包含任何嘢:數字、物件、或者抽象概念呀咁;一個集嘅元素 (element)可以係根據某個定義湊埋一齊嘅(好似係頭先嗰個例子咁),但係亦都可以係夾硬擺埋一齊、冇乜規律嘅。透過研究唔同集嘅數學特質,數學家發現佢哋可以精確又唔循環 (circular)咁定義數字同加減乘除呢啲基本嘅數學概念[ 2]
集(set)係一嚿包括一堆符合條件嘅元素嘅嘢。可以將佢諗成環保分類係既黃、藍、啡嘅桶。
元素(elements)係集入面嘅嘢,多數會叫佢做一個集入面嘅一粒嘢。用返上面既比喻,元素就係放入桶入面嘅垃圾。
黃桶入面裝嘅係鋁製品嘅,入面嘅垃圾一定係鋁製。同一道理,一個集入面嘅元素一定符合嘅條件。
自然數 :
N
:=
{
1
,
2
,
3
,
4
,
…
}
{\displaystyle \mathbb {N} :=\{1,2,3,4,\ldots \}}
整數 :
Z
:=
{
…
,
−
2
,
−
1
,
0
,
1
,
2
,
3
,
4
,
…
}
=
{
0
,
±
1
,
±
2
,
±
3
,
…
}
{\displaystyle \mathbb {Z} :=\{\ldots ,-2,-1,0,1,2,3,4,\ldots \}=\{0,\pm 1,\pm 2,\pm 3,\ldots \}}
Z
+
:=
{
0
,
1
,
2
,
3
,
4
,
…
}
{\displaystyle \mathbb {Z} ^{+}:=\{0,1,2,3,4,\ldots \}}
有理數 :
Q
:=
{
a
b
|
a
,
b
∈
Z
∧
b
≠
0
}
{\displaystyle \mathbb {Q} :=\{{\frac {a}{b}}|a,b\in \mathbb {Z} \land b\neq 0\}}
實數 :
R
:=
Q
∪
{
{\displaystyle \mathbb {R} :=\mathbb {Q} \cup \{}
}
{\displaystyle \}}
複數 :
C
:=
{
a
+
b
i
|
a
,
b
∈
R
,
i
=
−
1
}
{\displaystyle \mathbb {C} :=\{a+bi|a,b\in \mathbb {R} ,i={\sqrt {-1}}\}}
一個入面無元素嘅集係叫空集 (empty set)。
空集可以想像成為一個入面無嘢嘅紙袋,咁呢個袋就係一個空袋。對應就係空集。
空集集 (set of empty set)就係一個集,入面裝住一個空嘅集,即係
{
∅
}
{\displaystyle \{\varnothing \}}
∅
∈
{
∅
}
{\displaystyle \varnothing \in \{\varnothing \}}
∅
∈
∅
{\displaystyle \varnothing \in \varnothing }
可以幻想成,一個袋入面裝住一個袋,而入面個袋係無袋任何嘢。
如果有兩個集
X
{\displaystyle X}
Y
{\displaystyle Y}
相等(equal) ,即係話兩個集都有相同嘅元素。即係話,呢兩個袋入面裝住嘅嘢係一樣。
一般會以
X
=
Y
{\displaystyle X=Y}
X
≠
Y
{\displaystyle X\neq Y}
{
5
,
6
,
7
}
=
{
7
,
5
,
6
}
{\displaystyle \{5,6,7\}=\{7,5,6\}}
{
1
,
2
,
3
}
≠
{
1
,
2
}
{\displaystyle \{1,2,3\}\neq \{1,2\}}
{
∅
}
≠
∅
{\displaystyle \{\varnothing \}\neq \varnothing }
{
{
2
}
,
4
}
≠
{
2
,
4
}
{\displaystyle \{\{2\},4\}\neq \{2,4\}}
R
≠
N
{\displaystyle \mathbb {R} \neq \mathbb {N} }
2
N
=
{
0
,
±
2
,
±
4
,
⋯
}
{\displaystyle 2\mathbb {N} =\{0,\pm 2,\pm 4,\cdots \}}
如果集
X
{\displaystyle X}
X
{\displaystyle X}
有限集 (finite set)。而
X
{\displaystyle X}
基數 (cardinality)。
基數一般會以
|
X
|
{\displaystyle |X|}
X
{\displaystyle X}
{
∅
,
1
,
2
}
{\displaystyle \{\varnothing ,1,2\}}
3
{\displaystyle 3}
{
∅
,
1
,
{
4
,
2
}
}
{\displaystyle \{\varnothing ,1,\{4,2\}\}}
3
{\displaystyle 3}
以數學嘅角度嚟定義一個集,會以
{
x
|
x
{\displaystyle \{x|x}
P
}
{\displaystyle P\}}
|
{\displaystyle |}
|
{\displaystyle |}
{
x
∈
Z
:
4
≤
x
≤
6
}
{\displaystyle \{x\in \mathbb {Z} :4\leq x\leq 6\}}
{
4
,
5
,
6
}
{\displaystyle \{4,5,6\}}
{
x
∈
R
|
x
2
+
1
=
0
}
{\displaystyle \{x\in \mathbb {R} |x^{2}+1=0\}}
∅
{\displaystyle \varnothing }
{
x
∈
C
|
x
2
+
1
=
0
}
{\displaystyle \{x\in \mathbb {C} |x^{2}+1=0\}}
{
i
,
−
i
}
{\displaystyle \{i,-i\}}
0
=
{
}
{\displaystyle 0=\{\}}
1
=
{
0
}
=
{
{
}
}
{\displaystyle 1=\{0\}=\{\{\}\}}
2
=
{
0
,
1
}
=
{
{
}
,
{
{
}
}
}
{\displaystyle 2=\{0,1\}=\{\{\},\{\{\}\}\}}
.
.
.
{\displaystyle ...}
↑ Jech, T. (2013). Set theory . Springer Science & Business Media.
↑ Roitman, J. (1990). Introduction to modern set theory (Vol. 8). John Wiley & Sons.